第13章 大学物理机械波基础

1、1波波 动动第十三章第十三章（Wave）2第十三章第十三章 机械波基础机械波基础13.1 机械波的形成与传播机械波的形成与传播 13.2 平面简谐波的表达式平面简谐波的表达式 波动微分方程波动微分方程13.3 波的能量与能流波的能量与能流13.4 声波声波*13.5 惠更斯原理惠更斯原理13.6 波的叠加原理波的叠加原理 波的干涉波的干涉13.7 驻波驻波 半波损失半波损失13.8 多普勒效应多普勒效应3波动是振动的传播过程波动是振动的传播过程.振动是激发波动的波源振动是激发波动的波源.机械波机械波电磁波电磁波波动波动机械振动在机械振动在弹性弹性介质中的传播介质中的传播.交变电磁场在空间的传播

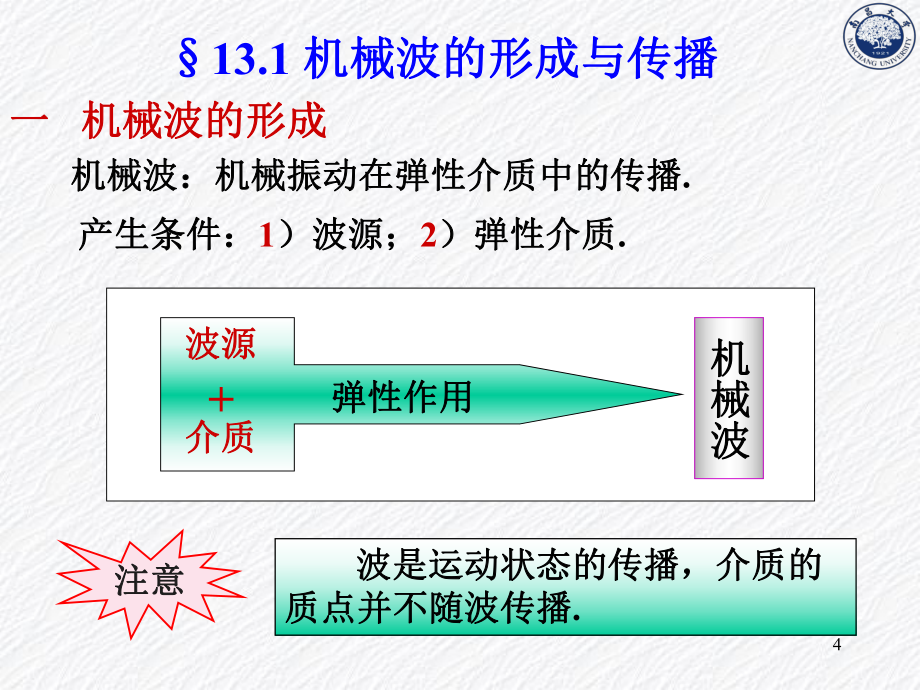
2、交变电磁场在空间的传播.两类波的不同之处两类波的不同之处v机械波的传播需机械波的传播需有传播振动的介质有传播振动的介质;v电磁波的传播可电磁波的传播可不需介质不需介质.2能量传播能量传播2反射反射2折射折射2干涉干涉2衍射衍射两类波的共同特征两类波的共同特征前言前言4波源波源介质介质+弹性作用弹性作用机械波机械波一一 机械波的形成机械波的形成产生条件：产生条件：1）波源；）波源；2）弹性介质）弹性介质. 波是运动状态的传播，介质的波是运动状态的传播，介质的质点并不随波传播质点并不随波传播.注意注意机械波：机械振动在弹性介质中的传播机械波：机械振动在弹性介质中的传播.13.1 机械波的形成与传播

3、机械波的形成与传播5横波：质点振动方向与波的传播方向相横波：质点振动方向与波的传播方向相垂直垂直的波的波.二二 横波与纵波横波与纵波 特征：具有交替出现的波峰和波谷特征：具有交替出现的波峰和波谷.6纵波：质点振动方向与波的传播方向互相纵波：质点振动方向与波的传播方向互相平行平行的波的波. 特征：具有交替出现的密部和疏部特征：具有交替出现的密部和疏部.7水的流动性和不可压缩性水的流动性和不可压缩性作二维运动作二维运动纵向运动纵向运动横向运动横向运动作作(椭椭)圆运动圆运动水水表面表面的波既非横波又非纵波：的波既非横波又非纵波：水波中水质元水波中水质元问：水波是问：水波是纵波还是纵波还是横波？横波

4、？答：水波即不是是纵波也不是横波是答：水波即不是是纵波也不是横波是混合波。混合波。x横横波波纵纵波波u8波线波线（wave line）表示波的传播方向的射线表示波的传播方向的射线（波射线）（波射线）波面波面（wave surface）媒质振动相位相同的点组成的面媒质振动相位相同的点组成的面（同相面）（同相面）波前波前（wave front）某时刻波到达的最前面的波某时刻波到达的最前面的波(振振)面面球面波球面波平面波平面波波波线线 波面波面波前波前波前波前波振面是波振面是平面的波平面的波三三 波线波线 波面波面 波前波前9*球球 面面 波波平平 面面 波波波前波前波面波面波线波线10四四 波长

5、波长 波的周期和频率波的周期和频率 波速波速2 波长波长 ：沿波的传播方向，两个相邻的、相：沿波的传播方向，两个相邻的、相位差为位差为 的振动质点之间的距离，即一个完整的振动质点之间的距离，即一个完整波形的长度波形的长度.2OyAA-ux112 周期周期 ：波前进一个波长的距离所需要：波前进一个波长的距离所需要的时间的时间.TT1TuTuu2 频率频率 ：周期的倒数，即单位时间内波：周期的倒数，即单位时间内波动所传播的完整波的数目动所传播的完整波的数目.2 波速波速 ：波动过程中，某一振动状态（即：波动过程中，某一振动状态（即振动相位）单位时间内所传播的距离（相速）振动相位）单位时间内所传播的

6、距离（相速）.u注意注意12波速波速 与介质的性质有关，与介质的性质有关， 为介质的密度为介质的密度.u如声音的传播速度如声音的传播速度sm4000sm343空气，常温空气，常温左右，左右，混凝土混凝土Gu Yu Bu 横横 波波固体固体纵纵 波波液、气体液、气体G切变切变模量模量Y弹性弹性模量模量B体积体积模量模量 紧紧拉拉的的绳绳索索, ,横横波波的的波波速速为为: : T Tu u ( (T T张张力力, , 是是= =质质量量线线密密度度) )13一、一、 简谐波简谐波（simple harmonic wave）波称为波称为简谐波简谐波（余弦波）（余弦波）如果波传播的扰动是简谐振动，这

7、样的如果波传播的扰动是简谐振动，这样的u一维平面简谐波的表达式（波函数）一维平面简谐波的表达式（波函数）以机械波的横波为例，以机械波的横波为例，设平面波沿设平面波沿 x方向以方向以速度速度 u 传播，传播， 媒质均匀、无限大，无吸收。媒质均匀、无限大，无吸收。13.2 平面简谐波的表达式平面简谐波的表达式 波动微分方程波动微分方程14或：沿波的传播方向或：沿波的传播方向, ,各质元的相位依次落后。各质元的相位依次落后。 抓住概念：某时刻某质元的相位（振动状态）抓住概念：某时刻某质元的相位（振动状态） 将在较晚时刻于将在较晚时刻于“下游下游”某处出现。某处出现。如何写出平面（一维）简谐波的波函数

8、？如何写出平面（一维）简谐波的波函数？ 须知三个条件：须知三个条件： 1. 某参考点的振动方程某参考点的振动方程( A, , ) 2. 波长波长 (或或 u)u T 3. 波的传播方向波的传播方向15点点 Pxtu 以速度以速度u 沿沿 x 轴正轴正向传播的平面简谐向传播的平面简谐波波。取平衡位置在取平衡位置在坐标原点坐标原点o o处的质处的质元作参考，元作参考，o o点的点的振动表达式为：振动表达式为：时间推时间推迟方法迟方法o0A cost ，设任意一点设任意一点 p 坐标为坐标为 x方法一：方法一：（或由运动的重复关系）（或由运动的重复关系）点点O 的振动状态的振动状态o0Acost 1

9、6t 时刻点时刻点 P 的运动的运动 时刻点时刻点O 的运动的运动则点则点P 振动方程振动方程:xtu- -0pxAcostu - - 波函数波函数02Acostx - - 或或: :0 xA costu - - Px* xuAA-O17点点 P 比点比点 O 落后落后的相位：的相位：Px* xuAA-O相位落后法相位落后法由相位关系：由相位关系：P点相位落后点相位落后波源波源o o的振动相位，所以就的振动相位，所以就在在o o点振动表达式的基础上点振动表达式的基础上改变相位因子就得到了改变相位因子就得到了P的的振动表达式振动表达式解法二：解法二：P Oxtuu 22ttxT 18 xuAA-

10、O点点 P 振动方程振动方程:02Acostx - - 波函数波函数0 xAcostu - - 02Acostx - - 19 波动方程的其它形式波动方程的其它形式( x,t )Acos(tkx) - - 2k波数波数0txA cos2 ()T - 0 xAcos2 ( t) - 02A cos(utx) - 0i( t kx)Re Ae - 波数波数-表示单位长度表示单位长度上波的相位变化上波的相位变化 波动方程的复数表示波动方程的复数表示20 质点的振动质点的振动速度速度，加速度加速度：xAsin(t)tu - - - v222xaAcos (t)ut - - - 2102A cos (

11、tx) - 1) )向向x轴轴负负向传播向传播02Acos (tx) 向向x轴轴正正向传播向传播平面谐波一般表达：平面谐波一般表达：02Acos ( tx)负负（正正）号代表向）号代表向 x 正正（负负）向传播的简谐波）向传播的简谐波讨论讨论222 2）波的表达式的物理意义）波的表达式的物理意义F当坐标当坐标 x 确定确定(即考察波线上的某一点即考察波线上的某一点) 表达式变成表达式变成t 关系关系 表达了表达了 x 点的振动点的振动 如图：如图：Ttox点的振动曲线点的振动曲线02Acos ( tx)23波线上各点的简谐运动图波线上各点的简谐运动图24F 当时刻当时刻 t 确定确定(即某一瞬

12、时即某一瞬时) 表达式变成表达式变成-x关系关系 表达了表达了 t 时刻空间各时刻空间各 点移分布点移分布波形图波形图 如图如图:xot 时刻的波形曲线时刻的波形曲线（空间周期）（空间周期）25 ab x = x2 - x1xu传播方向传播方向图中图中b点比点比a点的相位点的相位落后：落后：x 其其中中叫叫波波程程差差从波形图可看出在同一时刻，距波源从波形图可看出在同一时刻，距波源 o 分别分别为为x1、x2两质点的两质点的相位差相位差:（记住！）（记住！）x226F当当 x、t 都变化时都变化时 表达了波线上所有质元在各个时刻的位移，波函数表达了波线上所有质元在各个时刻的位移，波函数表示波形

13、沿传播方向的运动情况（行波）表示波形沿传播方向的运动情况（行波） 如图：如图：xot 时刻的波形曲线时刻的波形曲线（ 亦称空间周期）亦称空间周期）t + 时刻的波形曲线时刻的波形曲线txu t u所以波动方程描述了波形的传播所以波动方程描述了波形的传播27yxuO xuO( , )( , )t xtt xx cos2 ()txAT -2()2()txttxxTT - - - -txT tux t时刻时刻tt时刻时刻x28例例 求解波动问题示例求解波动问题示例1 1、已知波源、已知波源 x x0 0 的振动方程，写出波动方程的振动方程，写出波动方程 一平面简谐波以波速一平面简谐波以波速 u 沿沿

14、 x 轴正向传播轴正向传播 , 在离原点在离原点o 的的距离为距离为 x0 处的处的 p0 点，其振动方程为点，其振动方程为 y = A cos (t + )（1）求波动方程；）求波动方程；（2）求）求o点的振动方程。点的振动方程。 (1) p 点比点比 p0 点的振动落后点的振动落后 t=(xx0)/ u 因此因此)(cos)(cos0-uxxtAttAypp 为任一点，故波动方程为为任一点，故波动方程为)(cos0 - - - uxxtAyop0pxx0 x解解t)(0uxx-)/cos(00 uxtAy(2) x = 0 代入波动方程，得代入波动方程，得 o 点振动方程：点振动方程：29

15、2 2、已知波动方程作出、已知波动方程作出 t t 时刻的波形时刻的波形一横波沿一根弦线传播，其方程为一横波沿一根弦线传播，其方程为)2005(cos02.0txy-（SI制）制）（1 1）求振幅、波长、频率、周期及波速；）求振幅、波长、频率、周期及波速；（2）画出）画出 t = 0.0025 s 及及 t = 0.005 s 时刻弦的波形图；时刻弦的波形图； （1）解法一：对比法）解法一：对比法（3）若弦的线密度）若弦的线密度= 0.5 kg / m ，求弦上的张力大小。，求弦上的张力大小。)(cos.txy2005020- - ).(cos.400102020 xt- - 比较标准形式的波

16、动方程比较标准形式的波动方程)(2cos)(2cosuxtAxTtAy-可得：可得： A = 0.02 m , ,100 HzT = 0.01 su = 40 m / s ,m4.0解解例例30解法二：解法二：由定义求由定义求 21(5200 )(5200 )2xtxt -210.4xx - 解法一：解法一：描点法描点法 。将。将t值代入波动方程，值代入波动方程，再取再取x 值，算出对应位移值，算出对应位移y 值。然后描值。然后描点、连线，即得点、连线，即得 t 时刻波形图（时刻波形图（ 具体过具体过程略程略 ）。）。（2）作图）作图)2005(cos02. 0txy-31 解法二解法二: 意

17、义法。先作出意义法。先作出 t = 0 时刻的波形图，再算出时刻的波形图，再算出时间时间 t 内波传播的距离，平移波形即可。内波传播的距离，平移波形即可。t = 0t = 0.0025s经经 t = 0.0025 s , 波形右移波形右移 x = u t = 40 0. 0025 = 0.1 m = / 4经经 t = 0.005 s , 波形右波形右移移 x = u t = 40 0.005= 0.2m = / 2t = 0.005s(3)Tu 22400.5800TuN xyom4 . 0m8 . 0 xyom4 . 0m8 . 0 xyom4 . 0m8 . 032一平面简谐波以波速一平

18、面简谐波以波速 u = 200 msu = 200 ms-1 -1 沿沿x x轴正方轴正方向传播向传播 , ,在在t = 0 t = 0 时刻的波形如图所示。时刻的波形如图所示。 (2) (2) 求求t = 0.1s , x = 10 m t = 0.1s , x = 10 m 处质点的位移、振动速处质点的位移、振动速度和加速度。度和加速度。 t = 0 时时波形波形(1) (1) 求求 o o 点的振动方程与波动方程点的振动方程与波动方程 ；y y1 12 23 34 45 50.020.02o o(m(m）(m)(m)x xAm4Hzu504200 11002- - s 为方便起见为方便起

19、见, ,以下均以下均用用SISI制制, ,单位略去。单位略去。解解3 3、已知某时刻波形，写出波动方程、已知某时刻波形，写出波动方程例例u=200mu=200ms s-1-133 (1) o(1) o点振动方程点振动方程(2) (2) t = 0.1 s , x = 10 m 处质点处质点位移位移速度速度加速度加速度 2100cos02.0 t - - 2)200(100cos02. 0 xty波动方程波动方程:02)200(100cos02.0 - - xty 22)200(100sin10002.0 - - - - xttyv02)200(100cos)100(02.0222 - - -

20、- xttyat = 0 时波形时波形u = 200ms-1y123450.02o(m)(m)xov tAycos32 34)(2cos-xTtAy 1）波动方程？波动方程？2- 例例1 一平面简谐波沿一平面简谐波沿 O x 轴正方向传播，轴正方向传播， 已知振已知振幅幅 ， ， . 在在 时坐标时坐标原点处的质点位于平衡位置沿原点处的质点位于平衡位置沿 O y 轴正方向运动轴正方向运动 . 求求 0tm0 . 2m0 . 1As0 .2T0,0tyyv00 xt解解 ： 写出波动方程的标准式写出波动方程的标准式yAO2)m0 .2s0 .2(2cosm)0 .1 (-xty352）求求 波形

21、图波形图.x)msin( m)0.1(1-s0.1t)m(2cosm)0 .1 (1xy-波形方程波形方程s0.1t2)m0 .2s0 .2(2cosm)0 .1 (-xtyom/ym/x2.01.0-1.0 时刻波形图时刻波形图s0.1t363） 处质点的振动规律并做图处质点的振动规律并做图 .m5 . 0 x)scos(m)0 . 1 (1-ty2)m0 . 2s0 . 2(2cosm)0 . 1 (-xty 处质点的振动方程处质点的振动方程m5 . 0 x0m/y1.0-1.0s/t2.0Oy1234*1234处质点的振动曲线处质点的振动曲线m5 . 0 x1.037 例例2 一平面简谐

22、波以速度一平面简谐波以速度 沿直线传播沿直线传播,波波线上点线上点 A 的简谐运动方程的简谐运动方程 .s/m20u2(3 10 m)cos(4)Ayt-1）以以 A 为坐标原点，写出波动方程为坐标原点，写出波动方程m10 uTm1032-As5 . 0T02(3 10m)cos4()20 xyt-uABCD5m9mxo8m382BABAxx-B)s4cos()m103(12-tyB)m10s5 . 0(2cos)m103(2-xty2）以以 B 为坐标原点，写出波动方程为坐标原点，写出波动方程uABCD5m9mxo8m2(3 10m)cos(4)Ayt-393）写出传播方向上点写出传播方向上

23、点C、点点D 的简谐运动方程的简谐运动方程uABCD5m9mxo8m2(3 10 m)cos(4)Ayt-点点 C 的相位比点的相位比点 A 超前超前2(3 10m)cos(4)2CACyt-213(3 10m)cos(4)5t-点点 D 的相位落后于点的相位落后于点 A 29(3 10)cos(4)5-tmm102(310)cos(4 )2 -DADyt m404）分别求出分别求出 BC ，CD 两点间的相位差两点间的相位差22224.410CDCDxx- uABCD5m9mxo8m2(3 10)cos(4)-Aytm8221.610BCBCxx- m1041自测题：自测题：【解】：解】：（

24、1 1）求波长、频率、波速和周期？）求波长、频率、波速和周期？（2 2）说明）说明x=0 x=0时方程的意义并作图表示。时方程的意义并作图表示。已知一波动方程为已知一波动方程为005102y.sin(tx)m -（1）求解特征量，可采用比较法。将）求解特征量，可采用比较法。将题给方程改写成：题给方程改写成：0 051052xy.cos(t) -与一般式与一般式xyA cos( t)u -比较比较10 rad / s 515 7u. m / s 425 02. H Z 10 2T. s 3 14uT.m （2）由分析知：）由分析知：x=0时，方程时，方程0 05102y.cos(t) -表示位于

25、坐标原点的质点的振动方程表示位于坐标原点的质点的振动方程如图示：如图示：0.05t/sy/m00.10.2-0.0543如图示为某平面简谐波在如图示为某平面简谐波在t=0t=0时刻时刻的波形曲线图，求：的波形曲线图，求：（1 1）a,ba,b两点的运动方向？两点的运动方向？（2 2）简谐波的波动方程？）简谐波的波动方程？（3 3）P P点的振动方程？点的振动方程？abp【解】：解】：由由t=0时刻的波形时刻的波形曲线知：曲线知：10 450 20. m,Ts,.HZuT 自测题：自测题：0.04x/my/m00.20.4-0.040 08u.m / s 44（1）由于波沿）由于波沿x正方向传播

26、正方向传播a,b两点的运动方两点的运动方向：向：ab0.04x/my/m00.20.4-0.040 08u.m / s（2）设波函数为：）设波函数为：02yA cos(tx) -00 040 45.cos(.tx) -由由t=0的波形曲线知的波形曲线知, x=0质点：质点：0002cos 450002co s xA PO02 0 040 452y.cos( .tx)m -（3）对于）对于P点：点：30 304x.m 代入波函数得：代入波函数得：0 040 4y.cos( .t)m -曲线图：曲线图：0.04t/sy/m02.55-0.0446一一. .机械波的能量机械波的能量 能量密度能量密度

27、1. 机械波的机械波的能量能量每个质元振动所具有的动能每个质元振动所具有的动能每个质元形变所具有的势能每个质元形变所具有的势能之和之和m13.3 波的能量波的能量 和能流和能流以沿以沿 x 轴传播的轴传播的平面简谐横波平面简谐横波为例：为例：质量质量mx 质量线密度质量线密度l xx 1T2T47质元振动的动能质元振动的动能 22K11Emx22t() -PETlx质元形变势能质元形变势能由波的表达式由波的表达式:0 xA cos( t)u - - - 222K01xExA sin (t)2u(弹性势能弹性势能 =弹性拉力作的功弹性拉力作的功) 22()()lx二项式定理二项式定理展开略高次项

28、展开略高次项 211() 2lxxTu 48222P01xExA sin (t)2u -线元总机械能线元总机械能:KPE EE2220 xxA sin (t)u -xm mV 2220 xEA sin (t) Vu- 为绳子为绳子质量体密度质量体密度49振动系统：振动系统：kpkpEE EEconst.，系统与外界无能量交换。系统与外界无能量交换。波动质元：波动质元： ，kpkpconst.EEEE每个质元都与周围媒质交换能量。每个质元都与周围媒质交换能量。行波行波-通常指有振动状态和能量传播的波。通常指有振动状态和能量传播的波。（与驻波区别）（与驻波区别）讨论讨论503、平均能量密度、平均能

29、量密度220112Tww tAT d2、能量密度、能量密度（energy density）：）：2220-sin()WxwAtVu 22A （特征）（特征）- 单位体积中波的能量单位体积中波的能量- 一周期内能量密度的平均值一周期内能量密度的平均值51u t xS WPwu St2212Pw SuAu S 2.平均能流平均能流二、二、能流密度能流密度(功率密度功率密度) 波的强度波的强度 1.能流能流 单位时间内垂直通过某面积单位时间内垂直通过某面积 的的能量能量S- 一周期内能流的平均值一周期内能流的平均值WwV 52二、二、 能流密度能流密度(功率密度功率密度) 波的强度波的强度 3.能流

30、密度能流密度（energy flux density） 单位时间内垂直通过单位面积的能量单位时间内垂直通过单位面积的能量( (即通即通过单位面积的能流过单位面积的能流) )PwuS 4.平均能流密度（也称波的强度）平均能流密度（也称波的强度）2212PIwuA uS (记住记住!)2IA普适结论普适结论53 利用利用 和能量守恒，可以证明，和能量守恒，可以证明，221IA u2对无吸收媒质，有：对无吸收媒质，有：平面波平面波.const A球面波球面波rAAr1.const ， 柱面波柱面波rArA1.const ， r 场点到波源的距离场点到波源的距离三、平面波和球面波的振幅三、平面波和球面

31、波的振幅能流密度是矢量，其方向与波速方向相同。能流密度是矢量，其方向与波速方向相同。Iwu 54例例: :在均匀不吸收能量的媒质中传播的在均匀不吸收能量的媒质中传播的平面波在行进方向上振幅不变。平面波在行进方向上振幅不变。12SSS222211221122A uSA uS 12AA u1S2S所以：所以：1122w uSw uS 证证 介质无吸收，通过介质无吸收，通过两个平面的平均能流相等两个平面的平均能流相等.55例例 证明球面波的振幅与离证明球面波的振幅与离开其波源的距离成反比，并开其波源的距离成反比，并求球面简谐波的波函数求球面简谐波的波函数. 证证 介质无吸收，通过介质无吸收，通过两个

32、球面的平均能流相等两个球面的平均能流相等.1s2s1r2r1221ArAr 0 0cos()A rrytru - -1122w uSw uS 2222221122114422A urA ur 即即式中式中 为离开波源的距离，为离开波源的距离， 为为 处的振幅处的振幅.r0rr 0A56一平面简谐波在弹性媒质中传播时，一平面简谐波在弹性媒质中传播时，某一时刻在传播方向上媒质中某质某一时刻在传播方向上媒质中某质元在负的最大位移处，则它的能量元在负的最大位移处，则它的能量是：是： ？（1）动能为零，势能最大；）动能为零，势能最大；（2）动能为零，势能为零；）动能为零，势能为零；（3）动能最大，势能最

33、大；）动能最大，势能最大；（4）动能最大，势能为零。）动能最大，势能为零。222kP01xWWxA sin (t) 02u - p0 xAcostu -（2）0 xcost1u- -提示：提示：自测题：自测题：57一平面简谐波沿一平面简谐波沿x x的负方向传的负方向传播播, ,已知已知x=-1x=-1米处质点的振动米处质点的振动方程为方程为 , ,若波若波速为速为u,u,求此波的波动方程求此波的波动方程? ?()yAcost 【解】：解】：0 x1- -pxu1pxyAcos(t)u 取任一点取任一点P , 距距o点为点为x , 则则:方法一方法一:自测题：自测题：581cos ()pxyAt

34、u- - 0 xx1- - pu波动方程为波动方程为: :1xyAcos( t)u 取任一点取任一点P, 距距o点为点为x ,则则:波动方程为波动方程为: :1xyAcos(t)u 方法二方法二:59一平面简谐波沿一平面简谐波沿x x的正方向传播的正方向传播, ,已知已知x x1 1，x x2 2两点处的振动曲线分别如图示，两点处的振动曲线分别如图示，已知已知x x2 2xx1 1, ,且且 ，则这两点的，则这两点的距离？距离？21xx - - t/sy1 /m0t/sy2 /m0自测题：自测题：60【解】：解】：21xxt/sy1 /m0t/sy2 /m02x1xO2x 34x 32 x/m

35、y /m01x 2x61一平面简谐波，频率为一平面简谐波，频率为300HZ，波速为，波速为340米米/秒，在截面积为秒，在截面积为 的管内的管内空气中传播，若在空气中传播，若在10秒内通过截面的能量秒内通过截面的能量为为 ，求：（，求：（1）通过截面的平均能流；）通过截面的平均能流；（2）波的平均能流密度；（）波的平均能流密度；（3）波的平均）波的平均能量密度？能量密度？223.00 10 m- - 22.7 10 J- - 【解】：解】：（1）通过截面的平均能流）通过截面的平均能流:232 7 102 7 1010W.P.J / st-自测题：自测题：62（2）波的平均能流密度）波的平均能流

36、密度:32222.7 109.0 10/3 10PIJ m sS- - - - （3）波的平均能量密度）波的平均能量密度:PIwuS 2439.0 102.65 10/340IwJ mu- - - 6313.5 惠更斯原理惠更斯原理（Huygens principle） 前面讨论了波动的基本概念，前面讨论了波动的基本概念，现在讨论与现在讨论与波的传播特性有关的波的传播特性有关的现象、原理和规律。现象、原理和规律。 由于某些原因，由于某些原因，波在传播中，其波在传播中，其传播方传播方向、频率向、频率和和振幅振幅都有可能改变。惠更斯都有可能改变。惠更斯原理给出的方法原理给出的方法（惠更斯几何作图法

37、）（惠更斯几何作图法）是一种处理是一种处理波传播方向波传播方向的普遍方法。的普遍方法。64一、惠更斯原理一、惠更斯原理1、 原理内容原理内容: 媒质中任意波面上的各点，媒质中任意波面上的各点，都可看作是都可看作是发发射子波射子波（次级波）的（次级波）的波源波源（点源），其后（点源），其后的任一时刻，这些的任一时刻，这些子波面的包络面（包迹）子波面的包络面（包迹）就是波在该时刻的就是波在该时刻的波前波前。2、 原理的应用原理的应用:已知已知 t 时刻的波面时刻的波面 t+ t 时刻的波面，时刻的波面，从而可进一步给出波的传播方向。从而可进一步给出波的传播方向。65t+ t时刻波面时刻波面u t波

38、传播方向波传播方向t 时刻波面时刻波面平面波平面波t + t球面波球面波例如，均匀各向同性媒质内波的传播：例如，均匀各向同性媒质内波的传播：u t 66大量实验说明了惠更斯原理的正确性。大量实验说明了惠更斯原理的正确性。不足不足:(1)不能正确说明某些波动现象不能正确说明某些波动现象(如如干涉干涉)；二二. 波的衍射波的衍射（wave diffraction）衍射：衍射：波传播过程中，当遇到障碍物时波传播过程中，当遇到障碍物时，能绕过障碍物边缘而偏离直线传播的现象。能绕过障碍物边缘而偏离直线传播的现象。(2)没有说明各个子波在传播中对某一点没有说明各个子波在传播中对某一点的振动空究竟有多少贡献

39、。的振动空究竟有多少贡献。67入射波入射波衍射波衍射波障碍物障碍物入射波入射波衍射波衍射波障碍物障碍物a例如：例如：相对于相对于波长波长而言，而言，障碍物的线度越大障碍物的线度越大衍射现象衍射现象越不明显越不明显; ;障碍物的线度越小障碍物的线度越小衍射现象衍射现象越越明显。明显。波通过小孔波通过小孔波的衍射现象波的衍射现象可用惠更斯原理解释。可用惠更斯原理解释。68一一 波的叠加原理波的叠加原理2 几列波相遇之后，几列波相遇之后， 仍然保持它们各自原有的特征仍然保持它们各自原有的特征（频（频、波长、振幅、振动方向等）不变，并按照原来、波长、振幅、振动方向等）不变，并按照原来的方向继续前进，好

40、象没有遇到过其他波一样的方向继续前进，好象没有遇到过其他波一样.13.6 波的叠加原理波的叠加原理 波的干涉波的干涉69波的独立传播原理：波的独立传播原理：有几列波同时在媒质有几列波同时在媒质中传播时，它们的传中传播时，它们的传播特性（波长、频率播特性（波长、频率、波速、波形）不会、波速、波形）不会因其它波的存在而发因其它波的存在而发生影响生影响趣称：趣称：和平共处和平共处70细雨绵绵细雨绵绵独立传播独立传播71 （仍可辨出不同乐器的音色、旋律）（仍可辨出不同乐器的音色、旋律） 红红、绿绿光束空间光束空间交叉相遇交叉相遇（红红仍是仍是红红、绿绿仍是仍是绿绿）（仍能分别接收不同的电台广播（仍能分

41、别接收不同的电台广播） 听乐队演奏听乐队演奏 空中空中无线电波无线电波很多很多波的叠加原理：波的叠加原理：在它们相遇处，质元的位移为各波单独在该处在它们相遇处，质元的位移为各波单独在该处几列波可以保持各自的特点几列波可以保持各自的特点（方向、振幅、波长、频率）（方向、振幅、波长、频率） 同时通过同一媒质，同时通过同一媒质，产生位移的矢量和。产生位移的矢量和。日常现象：日常现象：72 叠加原理由波动方程的线性所决定，当叠加原理由波动方程的线性所决定，当波强度过大时波强度过大时 (如爆炸声如爆炸声,强激光强激光) ，媒质形，媒质形变与弹力的关系不再呈线性，叠加原理也变与弹力的关系不再呈线性，叠加原

42、理也就不再成立了。就不再成立了。 对于电磁波的情形：对于电磁波的情形：其解同样满足叠加原理。其解同样满足叠加原理。麦克斯韦方程组的各个方程都是线性的，则麦克斯韦方程组的各个方程都是线性的，则如果如果 D = E 和和 B = H 也是线性关系，也是线性关系，E或或H的每个分量的波动方程也是线性方程。的每个分量的波动方程也是线性方程。附注附注:73二二 、波的干涉现象、波的干涉现象 波叠加时在空间出现波叠加时在空间出现稳定的振动加强和减稳定的振动加强和减弱弱的分布叫的分布叫波的干涉。波的干涉。水波盘中水波的干涉水波盘中水波的干涉74频率相同、振动频率相同、振动方向相同、相位方向相同、相位差恒定的

43、两列波差恒定的两列波相遇时，使某些相遇时，使某些地方振动始终加地方振动始终加强，而使另一些强，而使另一些地方振动始终减地方振动始终减弱的现象，称为弱的现象，称为波的干涉现象波的干涉现象.波的干涉波的干涉75 相干条件：相干条件： 频率相同；频率相同； 振动方向相同；振动方向相同； 有恒定的相位差。有恒定的相位差。能产生干涉现象的能产生干涉现象的波称干涉波波称干涉波其波源称其波源称相干波源相干波源以下分析干涉现象的产生及确定以下分析干涉现象的产生及确定干涉加强干涉加强和和减弱减弱的条件的条件?76设两相距很近的相干波设两相距很近的相干波若两波源分别经若两波源分别经r1 , r2 , 到到P点相遇

44、点相遇,且振幅分别且振幅分别为为A1 , A2，则在，则在P点引起的分振动分别是：点引起的分振动分别是：111012cos()Atr-222022cos()Atr-1101010cos()SAt2202020cos()SAt1s2sP*1r2r77相位差相位差:2120102rr- P点合振动：点合振动：12cos()At合振幅合振幅121 22cosIIII I强度强度2212122cosAAAA A加强、减弱条件：加强、减弱条件：78l 加强条件加强条件 (干涉相长干涉相长 ) 2212122cosAAAA A由由知知2(0,1,2)kk 12AAA（干涉相长）（干涉相长）max121 2

45、2IIII I若若 A1 = A2 , 则则 Imax = 4 I1振动始终振动始终加强加强79l 减弱条件减弱条件 (干涉相消干涉相消)(21) (0,1,2)kk12AAA-（干涉相消）（干涉相消）min121 22IIII I- 若若 A1=A2 ,则则 Imin= 0干涉是能量的重新分布干涉是能量的重新分布振动始终振动始终减弱减弱80 加强条件加强条件 (0,1,)rkk 减弱条件减弱条件 (21)(0,1,)2rkk 20= 10特例：特例：2112222- -rrrrr波程差波程差相位差相位差例例13.4即讨论仅因波程差引起的相位差即讨论仅因波程差引起的相位差2121AAAAA-其

46、他其他r 其他其他r 81 例例 如图所示，如图所示，A、B 两点为同一介质中两相干波两点为同一介质中两相干波源源.其振幅皆为其振幅皆为5cm，频率皆为，频率皆为100Hz，但当点，但当点 A 为波为波峰时，点峰时，点B 恰为波谷恰为波谷.设波速为设波速为10m/s，试写出由，试写出由A、B发出的两列波传到点发出的两列波传到点P 时干涉的结果时干涉的结果.解解:15m20mABPmm22152025BP mm100.10100u 由题意可设由题意可设 A 的相位较的相位较 B 超前，则超前，则 .-BA25152 22010.1BABPAP- - - - - - - - - - - - - 点

47、点P 合振幅合振幅120AAA - - 8213.7 驻波驻波（standing wave）下面研究一种特殊的、常见的干涉现象下面研究一种特殊的、常见的干涉现象一、一、 驻波的形成驻波的形成能够传播的波叫行波能够传播的波叫行波（travelling wave）。）。两列两列振幅相等振幅相等的的相干相干的行波沿的行波沿相反方向相反方向传播而叠加时，就形成传播而叠加时，就形成，它是一种，它是一种常见的重要干涉现象。常见的重要干涉现象。驻波的形成驻波的形成832At = 0y0 x0t = T/8xx0t = T/20 xt = T/4波波节节波波腹腹/4- -/4x02A-2A/2xt = 3T/

48、8084 设两列行波分别沿设两列行波分别沿 x 轴的正向和反向传播，轴的正向和反向传播，1cos 2xyAt - -（）:x:x2cos 2xyAt （）二、二、 驻波表达式驻波表达式 驻波的特点驻波的特点设在设在 x = 0 处两波的处两波的初相均为初相均为 0，则：，则：1、驻波表达式、驻波表达式85yA合合A2A12x - -2x 21yyy AAA 21令令22 cosAAx合合如图如图 不具备传不具备传 播的特征播的特征表示各点都做简谐振动，振幅随位置不同而不同表示各点都做简谐振动，振幅随位置不同而不同.(,)( , )y tt xu ty t x 上式上式不满足不满足:.不是行波不

49、是行波.驻波的振幅与驻波的振幅与位置有关位置有关2cos 2cosxyAt各质点都在作同各质点都在作同频率的简谐运动频率的简谐运动860022cos2AxA波腹：波腹：振幅最大振幅最大2(0,1,)xkk(0, 1, 2,)2xkk与干涉加强条件得到的结果相同与干涉加强条件得到的结果相同2 波节波节波腹波腹87波节：振幅为零波节：振幅为零022cos0Ax2(21)(0, 1,)2xkk(21)(0, 1, 2,)4xkk 与干涉减弱条件得到的结果相同与干涉减弱条件得到的结果相同始终不始终不振动振动2 波节波节波腹波腹882.2.驻波的特点：驻波的特点：振幅各处不等大，振幅各处不等大，波腹波腹

50、 (2A) , 波节波节(0)。振幅：振幅：2cos 2 xA 驻波是分段的振动，设两相邻波节间为一段驻波是分段的振动，设两相邻波节间为一段,则则 相位中没有相位中没有x 坐标，坐标，故相位并不传播故相位并不传播 驻波。驻波。相位：相位：t cos 2cos2cos xyAt 相邻相邻波腹（节）波腹（节）间距间距 24相邻波相邻波腹腹和波和波节节间距间距89必一正一负。必一正一负。 相邻两段中各点振相邻两段中各点振动动 相位相反。相位相反。（为什么？）（为什么？）因为，相邻两段的因为，相邻两段的同一段中各点振同一段中各点振动相位相同；动相位相同；2cos2xAA 合xyo22-90合能流密度为

51、合能流密度为()0 w uwu - - 平均说来没有能量从节点处传播，平均说来没有能量从节点处传播，但各质元间但各质元间仍有能量的交换，两波节间能量应当守恒。仍有能量的交换，两波节间能量应当守恒。能量由两端向中间传，能量由两端向中间传，瞬时位移为瞬时位移为0，势能为，势能为0，能量由中间向两端传，能量由中间向两端传，动能最大。动能最大。动能动能势能。势能。 能量：能量：势能势能动能。动能。91例题：例题：如图所示可以是某时刻的驻波波形如图所示可以是某时刻的驻波波形,也也可以是某时刻的行波波形可以是某时刻的行波波形,图中图中 为波为波长长.就驻波而言就驻波而言, x1 , x2 两点间的相位差两

52、点间的相位差为为_;就行波而言就行波而言, x1 , x2 两点间的相位差两点间的相位差_?212()xx-y(m)x(m)A0-Ax1x2 92三、三、“半波损失半波损失”0反射波反射波 y1 入射波入射波 y1xn大大 波密媒质波密媒质n小小 波疏媒质波疏媒质相对相对而言而言（2）波）波疏疏波波密密，反射波有相位反射波有相位突变突变 ，（1）波密）波密波疏，波疏，反射波和入射反射波和入射波同相，无半波损失。波同相，无半波损失。93如下图示：如下图示：1111cos( 2)xyAt - - 入射波入射波1111 cos( 2 )xyAt 反射波反射波另外一种描述另外一种描述：（：（1 1）反

53、射端为自由端，无半波损失）反射端为自由端，无半波损失; ; （2 2）反射端为固定端，有半波损失。）反射端为固定端，有半波损失。94入射和反射波的波形如下：入射和反射波的波形如下：波腹波腹相位不变相位不变波疏媒质波疏媒质波密媒质波密媒质x驻波驻波波节波节驻波驻波相位突变相位突变 波疏媒质波疏媒质波密媒质波密媒质x2 入射波入射波入射波入射波反射波反射波反射波反射波波密波密波疏波疏波波疏疏波波密密95 波在一定边界内传播时就会形成各种驻波。波在一定边界内传播时就会形成各种驻波。如两端固定的弦，如两端固定的弦，L，3 , 2 , 12 nLnn nLn2 或或Lununn2 Tu系统的系统的固有频

54、率或简正频率固有频率或简正频率T 弦中的张力弦中的张力波速波速形成驻波必须满足以下条件：形成驻波必须满足以下条件： 弦的线密度弦的线密度四、两端固定的弦中的驻波四、两端固定的弦中的驻波96基频基频21 n =1二次二次谐频谐频n =222 三次三次谐频谐频n =323 每种可能的每种可能的稳定振动方式稳定振动方式称作系统的一个称作系统的一个固有振动或固有振动或简正模式简正模式注意：注意：驻波的波形驻波的波形和 能 量 都和 能 量 都“不传播不传播”，所以不是波所以不是波动，而是一动，而是一种特殊形式种特殊形式的振动。的振动。97一沿一沿x轴方向传播的入射波的表达式轴方向传播的入射波的表达式为

55、为 ，在，在x = 0处发生反射，处发生反射，反射点为一节点，求：（反射点为一节点，求：（1）反射波的表）反射波的表达式；（达式；（2）驻波的表达式；（）驻波的表达式；（3）波节、）波节、波腹的位置坐标。波腹的位置坐标。1cos2 ()txAT - -【解】：解】：例题例题（1）由题意知，波反射时有）由题意知，波反射时有 的相的相位突变，所以反射波的表达式为位突变，所以反射波的表达式为 2cos2()txAT 都都可可98（2）据波的叠加原理，驻波的表达式为：）据波的叠加原理，驻波的表达式为：12 cos()cos2 ()txtxAATT - - 222cos()cos()22xtAT 222

56、sinsinxtAT （3）形成波节的各点，振幅为零，则：形成波节的各点，振幅为零，则：992sin0 x 即：即：2xk .(0,1, 2,.)2xkk 形成波腹的各点，振幅最大，则：形成波腹的各点，振幅最大，则：2sin1x 0,.22xn -位置坐标：位置坐标：222sinsinxtAT 100(21).(0,1,.)4xkk 2(21)2xk 即：即：位置坐标：位置坐标：35,. (21)4444xn - - - - - 2 - -x 0 - -32 - -4 - -34 - -54 - -位置坐位置坐标如图标如图示：示：101例题：例题：沿弦线传播的一入射波在沿弦线传播的一入射波在x

57、=L处（处（B点）发生反射，反射点为自由端，点）发生反射，反射点为自由端，设振幅不变，且反射波的表达式设振幅不变，且反射波的表达式为为 ，则入射波，则入射波的表达式为：的表达式为： ？2cos2 ()xyAt y0LBx【解】：解】：B为反射波的波源，为反射波的波源，其振动方程为：其振动方程为：cos2 ()BLyAt O为为B点的波源，其振动方程为：点的波源，其振动方程为：12cos2 ()xLyAt - - 102cos2 ()OLLyAtu 2cos2 ()LAt 沿波线上任取一点，它到参考点的距离为沿波线上任取一点，它到参考点的距离为x，其振动方程为：其振动方程为：12cos2 ()x

58、LyAtu - - 2cos 2()xLAt - - 103发射频率发射频率s接收频率接收频率人耳听到的声音的频率与声源的频率相同吗？人耳听到的声音的频率与声源的频率相同吗？接收频率接收频率单位时间内观测者接收到的振动次单位时间内观测者接收到的振动次数或完整波数数或完整波数.s?只有波源与观察者相对静止时才相等只有波源与观察者相对静止时才相等.13.8 多普勒效应多普勒效应 (Doppler effect)104 多普勒效应：多普勒效应：由于波源和观察者的运动，由于波源和观察者的运动，而使观测的频率不同于波源频率的现象。而使观测的频率不同于波源频率的现象。一、机械波的多普勒效应一、机械波的多普

59、勒效应设设 运动在波源运动在波源 S 和观测者和观测者R的连线方向上，的连线方向上，以二者相向运动的方向为速度的正方向。以二者相向运动的方向为速度的正方向。uv vS 0v vR 0SR( (波的频率波的频率) )w（对媒质）（对媒质）（对媒质）（对媒质）S （波源频率）（波源频率）R （观测频率）（观测频率）105一一 波源不动，观察者相对介质以速度波源不动，观察者相对介质以速度 运动运动Rv106此时，此时，SwuSv vS = 0Rv vR vvuuu RRRSS()wuuv vR 0(R接近接近S)，SR v vR 0R,S反向反向(彼此远离彼此远离)运动，运动，v vs, v vR0,故有故有:v-RSSu. HZu 865 6警车驶离观察者时警车驶离观察者时,Vs 0,VR 0,则上式为则上式为:v836.2vRuHZu RSS- - - -(2)声波声波(警车警车)与客车上的观察者作同向运动与客车上的观察者作同向运动时时,观察者接收的频率为观察者接收的频率为:116复习指导复习指导2. 熟练掌握简谐波的描述熟练掌握简谐波的描述3. 掌握半波损失问题掌握半波损失问题4. 理解驻波的形成和它的几个特点理解驻波的形成和它的几个特点1. 弄清波动过程中相位领先和落后的概念弄清波动过程中相位领先和落后的概念