复变函数第15讲.

1、1分式线性映射公式:323211231231. (6.3.1)wwzzwwzzwwwwzzzz20(6.2.1)dd()azbabwadbcczdcdwadbczczd2现讨论在z平面内两个圆包围的区域的映射情况. 根据前面的讨论可知:(I)当二圆周上没有点映射成无穷远点时, 这二圆周的弧所围成的区域映射成二圆弧所围成的区域;(II)当二圆周上有一个点映射成无穷远点时, 这二圆周的弧所围成的区域映射成一圆弧与一直线所围成的区域;(III)当二圆周交点中的一个映射成无穷远点时, 这二圆周的弧所围成的区域映射成角形区域.3x1ii1C1C2y(z)O4解 所设的两个圆弧的交点为i与i, 且相互正交

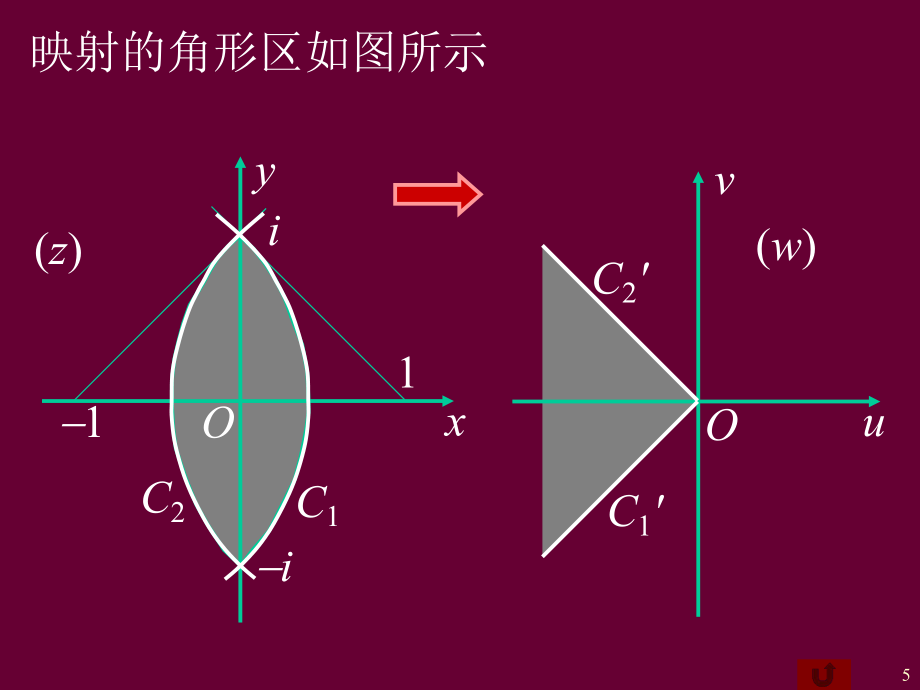
2、. 交点i映射成无穷远点, i映射成原点. 因此所给的区域经映射后映射成以原点为顶点的角形区域, 张角等于p/2.22)21 ()21 (1212, 121iiiwzC对应点是与正实轴的交点取此点在第三象限的分角线C1上. 由保角性知C2映射为第二象限的分角线C2.5映射的角形区如图所示x1ii1C1C2y(z)OC2C1Ouv(w)6例2 求将上半平面Im(z)0映射成单位圆|w|0映射成单位圆|w|0映射成单位圆|w|0映射成|w|0映射成单位圆|w|0映射成单位圆|w|1且满足w(2i)=0, arg w(2i)=0的分式线性映射.解 由条件w(2i)=0知, 所求的映射要将上半平面中的

3、点z=2i映射成单位圆周的圆心w=0. 所以由(6.3.2)得2.2iziwezi24( )e,(2 )iiw zzi因为故有(2 ).4iiwie13从而得所求的映射为2e,(2 )24arg(2 )0,.22iiziiwwieziwipp22ziwizi14例4 求将单位圆|z|1映射成单位圆|w|1的分式线性映射.x1y(z)OOuv(w)1aa115解 设z平面上单位圆|z|1内部的一点a映射成w平面上的单位圆|w|1的中心w=0. 这时与1| 1(0).,1,0,.zwwzwzwaaaa 点 对称于单位圆周的点应该被映射成平面上的无穷远点 即与对称的点 因此当时而当时满足这些条件的分

4、式线性映射具有如下的形式,111zzkzzkzzkwaaaaaaaakk其中16由于z平面上单位圆周上的点要映成w平面上单位圆周上的点, 所以当|z|=1,|w|=1. 将圆周|z|=1上的点z=1代入上式, 得|,1 |1 |1|11| |aaaa又因wk所以|k|=1, 即k=eij.这里j是任意实数.,1zzkwaa17因此, 将单位圆|z|1映射成单位圆|w|1的分式线性映射的一般表示式是e. (| 1)(6.3.5)1izwzjaaa. 1eee1ee|aaaajiiiiiw反之, 形如上式的映射必将单位圆|z|1映射成单位圆|w|1. 这是因为圆周|z|=1上的点z=ei (为实数

5、)映射成圆周|w|=1上的点:同时单位圆|z|1内有一点z=a映射成w=0.所以(6.3.5)必将单位圆|z|1映射成单位圆|w|0的分式线性映射.解 由条件w(1/2)=0知, 所求的映射要将z=1/2 映射成|w|0映射成|w2i|2且满足条件w(2i)=2i, arg w(2i)p/2的分式线性映射.解 容易看出, 映射z=(w2i)/2将|w2i|2映射成|z|0映射成|z|1且满足z(2i)=0的映射易知为,41e2)2(22e2222eiiwiziziwiziziiiz由此得故有21.22)1 (22222. 0,2)2(arg.2)4arg()e2arg()2(arg,41e2)

6、2(22e22izziwiziziwiwiiwiiwiziziwiii或于是所求映射为从而得由于已知pp222i(z)O(z)2i(w)izziw22)1 (2iziz22zw=2(i+z)234 几个初等函数所构成的映射241. 幂函数 w=zn(n2为自然数)在z平面内处处可导, 它的导数是1ddnnzzw0ddzw因而当z0时, 所以, 在z平面内除去原点外, 由w=zn所构成的映射处处共形.映射的特点是: 把以原点为顶点的角形域映射成以原点为顶点的角形域, 但张角变成了原来的n倍25O(z)0O(w)n0w=zn(z)(w)OOnp2上岸下岸w=zn26例1 求把角形域0arg zp/

7、4映射成单位圆|w|1的一个映射.解 z=z4将所给角形域0arg z0. 又从上节的例2知, 映射. 1|44izizwwiiw所求映射为因此圆将上半平面映射成单位zz27(z)O4pO(z )1(w)z z4iiwzzizizw4428例2 求把下图中由圆弧C2与C3所围成的交角为a的月牙域映射成角形域j0arg wj0+a的一个映射.aj0(w)O1C1C2a(z)Oii29aO(z)aj0(w)O1C1C2a(z)Oiiizizizzj0eiw izizewi)2(0pj130解 先求出把C1,C2的交点i与i分别映射成z平面中的z=0与z=, 并使月牙域映射成角形域0argzp;再把

8、这角形域通过映射w=exp(ij0)z转过一角度j0, 即得把所给月牙域映射成所给角形域的映射.将所给月牙域映射成z平面中的角形域的映射是具有以下形式的分式线性函数:izizkz其中k为待定的复常数.31.arg0,., 1.111)2(1100izizeiziziewCiziziikikiikzCizizkiipjjazzzzzz由此得所求的映射为映射成角形域它把所给的月牙域根据保角性平面上的正实轴映射成就把映射这样使取映射成上的点此映射把32例3 求把具有割痕Re(z)=a, 0Im(z)h的上半平面映射成上半平面的一个映射.xOy(z)C(a+ih)B DaOuv(w)aha a+hBC

9、D33xOy(z)C(a+ih)B DaOuv(w)aha a+hBCDO(z1)CB Dihh2CO BD(z2)COBh2D(z3)O(z4)CBDh+hz1=zaz2=z12z3=z2+h234zz w=z4+aahazw22)(34解 不难看出, 解决本题的关键显然是要设法将垂直于x轴的割痕的两侧和x轴之间的夹角展平. 由于映射w=z2能将顶点在原点处的角度增大到两倍, 所以利用这个映射可以达到将割痕展平的目的.首先, 把上半z平面向左作一个距离为a的平移:z1=za.第二, 再应用映射z2=z12, 便得到一个具有割痕h2Re(z2)+, Im(z2)=0的z2平面.第三, 把z2平

10、面向右作一距离为h2的平移: z3=z2+h2, 便得到去掉了正实轴的z3平面.35ahazwwazwazzzz2244434)(:.,:,.,映射就得到所求出把所有的映射复合起来平面中的上半平面便得到的平移平面向右作一距离为把最后平面便得到上半通过映射第四362. 指数函数 w=ez 由于在z平面内w=(ez)=ez0所以, 由w=ez所构成的映射是一个全平面上的共形映射. 设z=x+iy, w=reij, 则r = ex,j = y,(6.4.2)由此可知: z平面上的直线x=常数, 被映射成w平面上的圆周r=常数; 而直线y=常数, 被映射成射线j=常数.带形域0Im(z)a映射成角形域0arg wa. 特别是带形域0Im(z)2p映射成沿正实轴剪开的w平面:0arg w2p.它们间的点是一一对应的.37aiOxy(z)arg w=auOv(w)2piOxy(z)Ouv(w)w=ezz=lnw38由指数函数w=ez所构成的映射的特点是: 把水平的带形域0Im(z)a(ap)映射成角形域0arg wa. 因此, 如果要把带形域映射成角形域, 常常利用指数函数.39例4 求把带形域0Im(z)p映射成单位圆|w|0. 而根据(6.3.4)又知:iiwwiiwzzee. 1|0)Im(因此所求的映射为成单位圆映射将平面的上半平面映射zzz40例5 求把带形