材料加工中的数值模拟方法-微观组织数值模拟(8)

1、材料加工过程的数值模拟微观组织数值模拟(VIII)任课教师: 王锦程Office：公字楼216Tel O)Email ： Cellular Automata元胞自动机p基本概念与思想基本概念与思想p应用应用pMeso-CApMicro-CA“生命游戏生命游戏” 对“活”格，如果在其邻格中有2个或3个是“活”格，则下一时刻继续“活”下去，否则就“死” 对“死”格，如果在其邻格中有3个是“活”格，就变为“活”，否则就继续“死”一个由许多相同正方形方格组成的棋盘上每个方格有八个邻格，每个格内用黑圈代表“活，空格代表“死”。游戏规则：John H. Conway几个简单结果

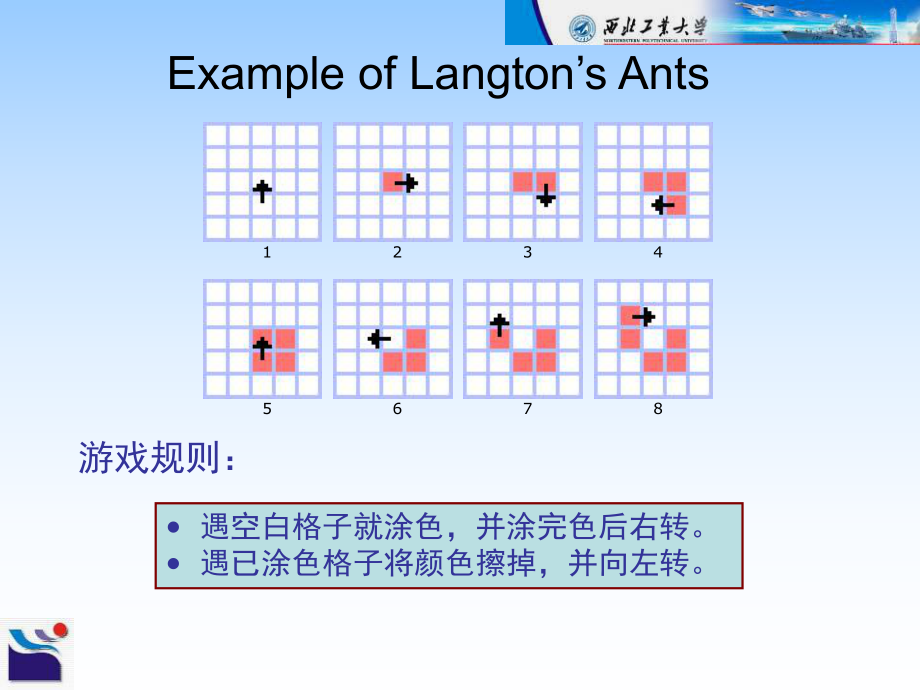
2、几个简单结果Example of Langtons Ants12346785 遇空白格子就涂色，并涂完色后右转。 遇已涂色格子将颜色擦掉，并向左转。游戏规则：Virtual Ant After Many Iterationsp Though the movement of the ant is deterministic, the first 10,000, or so, iterations seem chaotic and unpredictable. Eventually, however, the ant begins to form a road. 5,000 it.10,000 i

3、t.12,000 it.典型的行为 简单规则，简单初始条件下1、规律2、嵌套3、随机4、有局部结构简单系统可以产生所有可能行为Cellular Automata描述复杂系统在离散的时间和空间上演化规律的一种算法.在一个元胞自动机模型中,体系被分解成有限个胞,同时把时间离散化为一定间隔的步,每个胞的所有可能状态也划分为有限个分立的状态。每个胞在前后时间步的状态转变按一定的演变规则来决定,这种转变是随时间不断地对体系各胞同步进行。因此一个胞的状态受其邻居胞的状态的影响,同时也影响着邻居胞的状态,局部之间互相作用,相互影响。通过这一定的规则变化而整合成一总体行为。 元胞自动机基本思想元胞自动机基本思

4、想p最早由Von Neumann和Stanislaw Ulam提出来;p目前广泛应用于模拟各种物理系统和自然现象，如流体运动、生物模式形成、雪崩、地震等等;p优点在于省去了用微分方程作为过渡而直接通过制定规则来模拟非线性物理现象.元胞自动机 Cellular AutomataStanislaw Ulam (1909-1984)Alan Turing (1912-1954) John von Neumann (1903-1957)p元胞自动机（Cellular Automata）是一种时间、空间、状态都离散，空间上相互作用及时间上的因果关系皆局部的网格动力学模型。这一思想最早由计算机创始人，著名

5、数学家V. Neumann 提出，应用于生物体发育中细胞的自我复制。p1970 年，剑桥大学的J. H. Conway利用元胞自动机法编制了一个名为“生命”的游戏程序，并由M. Gardner 通过科学美国人介绍到全世界。该游戏通过几条简单“生死”规则的组合，细胞在网格中就可以出现无法预测的延伸、变形、停止和周期性变化的复杂模式。这种意想不到的结果吸引了大批计算机科学家研究“生命”程序的特点，最终证明这个程序与Turing 机等价，也就是说给定适当的初始条件，“生命”模型可以模拟任何一种计算机。CA 方法的产生和发展方法的产生和发展p20 世纪80 年代，物理学家、计算机科学家对元胞自动机模型

6、的兴趣大增。S. Wolfram对CA 的贡献很大，他引入动力系统的思想理论和研究方法，对元胞自动机进行了系统的研究，用熵来描述其演化行为，并将元胞自动机按动力学行为分为平稳型、周期型、混沌型和复杂型，分别对应于人们已经熟悉的不动点、周期行为、混沌状态和自组织现象。p1986 年，U. Frish等人发表了代替Navier-Stocks 方程的格子气自动机，这种计算机比常见的Navier-Stocks (N-S)方程数值法快得多，开辟了流体力学的一个全新领域。p随后L. O. Chuan将CA 引入神经网络，建立细胞神经网络模型。另外，由于元胞自动机的运算每次不涉及全局的状态，专家们正在考虑按

7、照这种思想设计新一代的计算机，采用大规模并行结构, 最终目的是以较小的代价达到超级计算机的能力。主要特征p空间是离散的；p时间是离散的；p状态取值是离散的；p演化的运算规则是局域的(一般情形）；利用大量的简单的元件，通过简单的连接和简单的运算规则，在时空中并行地持续运行，以模拟出复杂而丰富的现象。不同于一般的动力学模型，元胞自动机不是由严格定义的物理方程或函数确定，而是用一系列模型构造的规则构成 元胞自动机在的应用元胞自动机可用来研究很多一般现象。其中包括通信、信息传递(Communication)、计算(Computation)、构造 (Construction)、生长(Growth)、复制

8、(Reproduction）、竞争(Competition)与进化(Evolution)等。同时。它为动力学系统理论中有关秩序 (Ordering)、紊动 (Turbulence)、混沌 (Chaos)、对称破缺(Symmetry-Breaking)、分形(Fractal)等系统整体行为与复杂现象的研究提供了一个有效的模型工具。 元胞自动机自产生以来，被广泛地应用到社会、经济、军事和科学研究的各个领域。应用领域涉及社会学、生物学、生态学、信息科学、计算机科学、数学、物理学、化学、材料科学，地理、环境、军事学等。 元胞自动机在材料组织模拟研究中的应用p凝固与结晶p晶粒长大与再结晶p相沉淀与相分解

9、p位错花样的形成Al-4wt%Cu alloy 6301200, x=1 m, G=2000K/m, T=3K Calculation time: 11 hours, PC Pentium IV In718-5Nd alloy alloy, cooling rate of 5 K/s, 250250250, x=1m) Simulated peritectic microstructure evolution1.25 s1.4 s2.5 s4.5 sFe-0.3wt%C alloy, domain: 260260, cell size: 2 m,cooling rate: 10 K/s, pe

10、ritectic undercooling: 2K0.3 s0.6 s Uin=0.03m/s Vin=0Uin=0.02m/s Vin=0.02m/sWithout flowThe simulated microstructure evolution during the deformed austenite decomposition into ferriteSimulated overall transformation behavior using the CA model: (a) the overall transformation kinetics; (b)(d) the tem

11、poral evolution of the microstructure (left) and the carbon concentration field (right) during the transformation.Modeling snowflakesCellular automaton modelC.A. Reiter, Chaos, Solitons and Fractals 23 (2005) 111111191=ice1=water1) Localization of receptive sites (ice or neighbours of ice)2) Values

12、of sites are update (diffusion + )3) The background level is chosen Shapes resemble snowflakes but no physical interpretationp 晶粒长大p 枝晶生长CA应用实例1993 年, Rappaz 和Gandin首先建立了研究凝固组织形成过程的二维CA模型。1994 年, Gandin 和Rappaz提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE 模型。1997 年, Dilthey等提出了基于凝固界面处热量或溶质守恒关系计算枝晶生长速度的

13、模型, 将CA模型的应用范围由介观尺度推进到了微观尺度.1999 年, Nastac用溶质守恒条件计算固液界面的迁移速度, 进一步发展了CA模型.2001 年, Zhu 等发展了改进的CA 模型(MCA模型），2004年进一步推广到包含熔体对流的合金凝固过程, 发展了一个二维MCA-传输模型。 2007 年, Zhu等通过构建虚拟固液界面来模拟任意择优生长方向的枝晶形貌。CA模型在凝固微观组织模拟中的发展历程晶粒生长Gandin-Rappaz（1993） 连续形核模型描述形核过程； 随机分配形核位置以及晶粒取向； KGT模型计算固液界面生长速度。不考虑热传输和结晶潜热的释放（温度均匀）； 不考

14、虑凝固过程中浓度场的变化。晶粒的生长形状可大致认为是方形(二维)。首先将铸件在二维平面上划分为规则的网格单元(通常为三角形或四边形)，标记每个单元的最相邻单元，次相邻单元。A为网格单元的一个形核结点，它在某一时刻tN结晶形核。晶粒长大方向与x轴夹角为(可由代表晶向的整数值q转换得到)。在t时刻，晶粒的半径，即图中阴影四边形的半对角线长L(t)，为枝晶尖端长大速率v(T(t)从tN到t时间段上的积分:晶粒生长到达t，时刻，由A结点形核长大的四方形晶粒接触到四个相邻单元B1, B2, B3, B4。这时，晶粒半对角线长(半径)L(tB)与l相等，此时单元B1B4凝固，其索引值被赋予一个与原始结点A

15、相同的整数值q。sincoslll为CA网格单元间距晶粒生长但实际上，枝晶的长大分枝机制并不是一个确定的过程，所以，这里也可采用类似的Monte Carlo随机手段，首先计算晶粒长大概率Pg将Pg与一随机数发生器n(0rr，则B1B4单元被捕获，凝固完毕。B的四个单元结点继续长大，将在下一时刻tC捕获C的八个结点，依次类推将捕获D的十二个结点。晶粒生长形核形核过程采用概率性的均匀成核。在一个时间步内，在模壁表面与熔体体积内，新晶粒的成核密度分别增加ns与nv ，其表达式为 TdfTddnnTdfTddnnsTTTsssTTTvv11 0/1*SLLLsCCCCf在熔体内部及模壁表面的成核概率p

16、v与pS:SnpVnpssvv对于每一个元胞，取一个随机数r(0r1)，如果该随机数小于成核概率，这个元胞由液态转变为固态，同时生长状态数变为i(表示开始生长)，状态数随机取一个从1到100的正数，代表某一结晶取向。形核取向式中v, s分别代表样品单位元胞的熔体体积与表面积。 液态元胞有固态近邻元胞 液态元胞的平衡温度要低于凝固温度 对满足上述条件的液态元胞上生成一随机数，如果它小于该元胞固态近邻元胞在该方向的“捕获”概率，这个液态元胞转化为固态。 如果考虑温度场和成分场，则这些液态元胞析出它们的溶质到近邻的液态元胞，并释放凝固潜热。是否转化为固态的条件模型中，元胞的状态由元胞的状态数(取0表

17、示液相，1表示固/液界面，2表示固相)，晶粒生长的长度、温度场值确定。对于一个给定的元胞，它的温度是按一个给定的冷却率T降低的。元胞状态 kcctpvkrtcVRPIvkPIvkmcPIvcLTTTTT2111 0Tc 溶质过冷Tt 热过冷Tr 曲率过冷Tk 动力学过冷Rapid SolidificationCA模型的核心问题是要确定转化规则。而在晶粒长大（枝晶生长）中，确定转化规则的核心是要得到界面的生长速度.RVT界面生长速度KGT（ Kurz-Giovanola-Trivedi）模型模型（柱状晶）（柱状晶）在枝晶定向(柱状)生长过程中，枝晶尖端液相中溶质富集，有较大的浓度梯度，从而产生较大的成分过冷度Tc，热过冷度Tt和动力学过冷度Tk相对一般较小，常被忽略不计。因此，