数字电路卡诺图课件

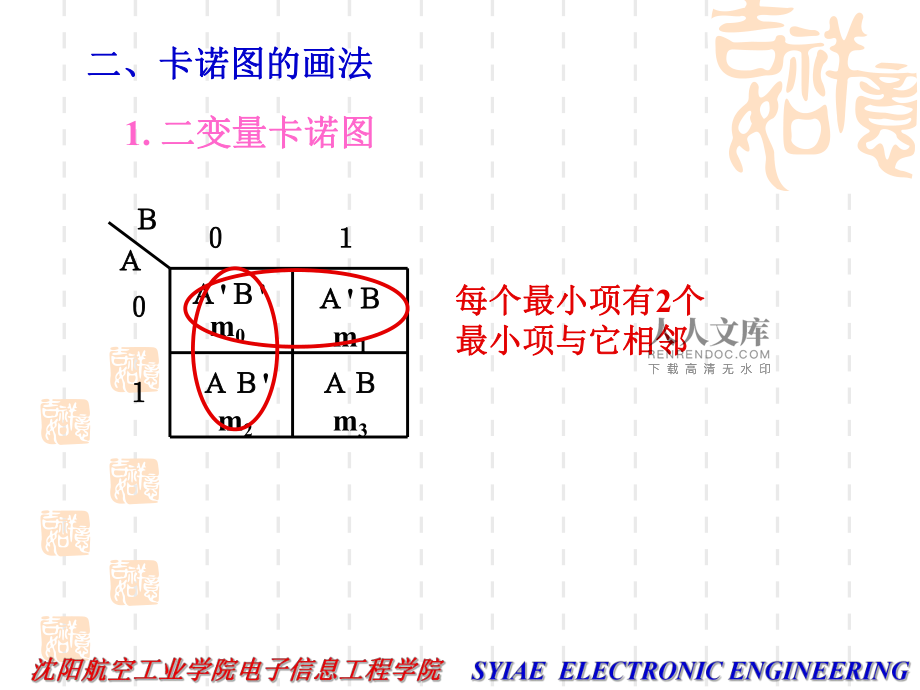
1、卡诺图化简法卡诺图化简法一、什么是卡诺图一、什么是卡诺图将将n变量的全部变量的全部最小项最小项各用一个小方块表示，各用一个小方块表示，并使具有并使具有逻辑相邻性逻辑相邻性的最小项在几何位置上也相邻的最小项在几何位置上也相邻的排列，所得到的图形称为的排列，所得到的图形称为n变量最小项的变量最小项的卡诺图卡诺图。 因为这种表示方法由美国工程师因为这种表示方法由美国工程师卡诺卡诺（M.Karnaugh）首先提出，因此这种）首先提出，因此这种图形称为图形称为卡诺图卡诺图（Karnaugh Map）。）。两个最小项仅有一个变量是不同，其余的相同m3m0m1m2二、卡诺图的画法二、卡诺图的画法1. 二变量

2、卡诺图二变量卡诺图每个最小项有每个最小项有2个个最小项与它相邻最小项与它相邻00011110m0m1m2m3m4m5m6m7每个最小项有三个每个最小项有三个最小项与它相邻最小项与它相邻确保几何位置相邻的两个最小项逻辑上相邻BD000001011110m0m1m2m3m4m5m6m71110m12m13m15m14m8m9m11m10每个最小项有每个最小项有4个个最小项与它相邻最小项与它相邻最左列的最小项与最左列的最小项与最右列的相应最小最右列的相应最小项也是相邻的项也是相邻的最上面一行的最小最上面一行的最小项与最下面一行的项与最下面一行的相应最小项也是相相应最小项也是相邻的邻的三、用卡诺图表示

3、逻辑函数三、用卡诺图表示逻辑函数(一一) 由逻辑函数画出卡诺图由逻辑函数画出卡诺图 1. 根据根据标准与标准与或式或式画卡诺图画卡诺图方法：方法： 将逻辑函数化成最小项之和形式；将逻辑函数化成最小项之和形式； 在卡诺图上，对应于函数式中最小项的位置在卡诺图上，对应于函数式中最小项的位置填填1，其余位置填，其余位置填0。即任何一个逻辑函数都等于它的卡诺图即任何一个逻辑函数都等于它的卡诺图中填入中填入1的那些最小项之和。的那些最小项之和。 逻辑函数最小项表达式中含有的逻辑函数最小项表达式中含有的最小项最小项，在，在卡诺图相应小方格中填卡诺图相应小方格中填“1”，其余则填，其余则填“0”。此。此时的

4、卡诺图就是对应于该函数的卡诺图。时的卡诺图就是对应于该函数的卡诺图。例：画例：画Y=A+BC的卡诺图。的卡诺图。解：最小项之和形式为：解：最小项之和形式为：34567mmmmmBCACABCABABCABCBCAABCCABCABABCABC) AA(BC) CC)(BB(AY 卡诺图为：卡诺图为：1111010015111098641mmmmmmmmDCABCDABDCABCDABCDABABCDDBCABCDADCBA) DD)(CC( ABCD) BB(AD) CC(BADCBAY 解：解：最小项之和形式为：最小项之和形式为：的卡诺图。的卡诺图。例：画例：画ABACDBDADCBAY B

5、D00000101111001001010111000101111m1m4m6m15m8m9m11m102. 由由一般逻辑式一般逻辑式直接画卡诺图直接画卡诺图先将函数变换为与或表达式（先将函数变换为与或表达式（不必变换为不必变换为最小项之和的形式最小项之和的形式），然后在卡诺图上与每一个），然后在卡诺图上与每一个乘积项所包含的那些最小项（该乘积项就是这些乘积项所包含的那些最小项（该乘积项就是这些最小项的公因子）相对应的方格内填入最小项的公因子）相对应的方格内填入1，其余，其余的方格内填入的方格内填入0。解：解：这是四变量逻辑函数，画四变量卡诺图。这是四变量逻辑函数，画四变量卡诺图。分项看：分项

6、看：1111111111)CB)(DA(Y CBDAY ABC D00011110001100010000111001101101变换为与变换为与或表达式或表达式公因子为公因子为 公因子为公因子为 说明说明：如果求得了函数的反函数：如果求得了函数的反函数 ，则对则对 中所包含的各个最小项，在卡诺图相中所包含的各个最小项，在卡诺图相应方格内填入应方格内填入0，其余方格内填入，其余方格内填入1。ABCCABCABY ABCBCABCACBACBAY 四、用卡诺图化简逻辑函数四、用卡诺图化简逻辑函数、化简的依据、化简的依据A+AB=A因为卡诺图上下左右任意相邻的两格因为卡诺图上下左右任意相邻的两格之

7、间，只改变一个变量，因此，当两个相之间，只改变一个变量，因此，当两个相邻项为邻项为“”时，可合并为一项。其依据时，可合并为一项。其依据是是基本公式：基本公式：、化简的方法、化简的方法 圈相邻圈相邻2个个“”，可消去改变值的，可消去改变值的1个个变量；变量； 圈相邻圈相邻4个个“”，可消去改变值的，可消去改变值的2个个变量；变量； 圈相邻圈相邻8个个“”，可消去改变值的，可消去改变值的3个个变量；变量； 圈相邻圈相邻n个个“”，可消去改变值的，可消去改变值的n个个变量；变量；例：圈相邻例：圈相邻2个个“”,可以合并为一项，并消去一个可以合并为一项，并消去一个变量（消去变量（消去互为反变量互为反变

8、量的因子，保留公因子）的因子，保留公因子） 。CB)AA(CBCABCBAY CDB)AA( CDBCDABCDBAY ABD)CC( ABDABCDDABCY DBDB)AA(D)CC( ABD)CC( BACDABDCABCDBADCBA 11 11BDBD)AA(D)CC(ABD)CC(BAABCDDABCBCDADBCA DBBDDBY ABC D00011110000110011001111001100110B DBDBDBY ABCD00011110000100011111110110100100 AB C000111100111110110CC) ABABBABA(CABABCB

9、CACBA BB)ACACCACA(ABCABCBCABCA BADCBDCBY BDDCBAY DY DY DAY 1111 先圈大，后圈小，即先圈先圈大，后圈小，即先圈8格，后圈格，后圈4格、格、2格格保证所得乘积项数目最少且每个乘积项保证所得乘积项数目最少且每个乘积项包含的因子最少；包含的因子最少； 必须是相邻方格的必须是相邻方格的“1”，才能圈起来；，才能圈起来； 允许方格重叠被圈允许方格重叠被圈(A+A=A)，但每个圈内，但每个圈内必须有一个以上（含）的必须有一个以上（含）的“1”未被其它圈圈过；未被其它圈圈过； 没有相邻项的没有相邻项的“1”，要单独圈出。，要单独圈出。 不能漏掉任

10、何一个标不能漏掉任何一个标“1”的方格。的方格。画圈的原则：画圈的原则：3、卡诺图化简举例、卡诺图化简举例步骤：步骤：根据逻辑函数式画卡诺图；根据逻辑函数式画卡诺图；合并最小项；合并最小项；化成最简与或表达式；化成最简与或表达式；CDABBCDDABCDBCACBAY CDABCBABDY )15,13,12,11, 9 , 6 , 5 , 3 , 1 , 0(),( imDCBAFYiiDCY BCDA AD DB CBA ABC CBBCCAACY BCCAABY BACBACY DAY DA)DA()Y(Y CDACABDCDACABDABCY 式式下下式式化化为为最最简简与与或或逻逻辑

11、辑例例：用用卡卡诺诺图图化化简简法法将将AD求求原函数原函数时圈的是时圈的是“1”，求，求反函数反函数时圈的时圈的是是“0”。其消去变量个数和画圈的规律都相同。其消去变量个数和画圈的规律都相同。化简时，圈化简时，圈“1”还是圈还是圈“0”，根据需要，哪个简，根据需要，哪个简单，采用哪个。（当单，采用哪个。（当0的数目远小于的数目远小于1的数目，或的数目，或要将函数化为最简的与或非式，或要求要将函数化为最简的与或非式，或要求Y的化简结的化简结果）果）两点说明：两点说明： 在有些情况下，最小项的圈法不只一种，得到在有些情况下，最小项的圈法不只一种，得到的各个乘积项组成的与或表达式各不相同，哪个是最的各个乘积项组成的与或表达式各不相同，哪个是最简的，要经过比较、检查才能确定。简的，要经过比较、检查才能确定。 AB