第三章-热辐射的基本规律

1、第三章第三章 热辐射的基本规律热辐射的基本规律3.1 3.1 发光的种类发光的种类辉光放电辉光放电 弧光（电弧）放电弧光（电弧）放电 2，气体放电（电致气体放电发光），气体放电（电致气体放电发光）火花放电火花放电低（气）压放电低（气）压放电常（气）压放电常（气）压放电 1，化学发光，化学发光 直接发光直接发光简接发光简接发光 3，场致发光（电致发光）：载流子复合发光，场致发光（电致发光）：载流子复合发光 发光二极管（发光二极管（LED）电致发光显示屏电致发光显示屏6，热辐射，热辐射5，光致发光，光致发光 4，电（子）激发发光，电（子）激发发光如：电子显象管如：电子显象管光激发发光光激发发光荧光

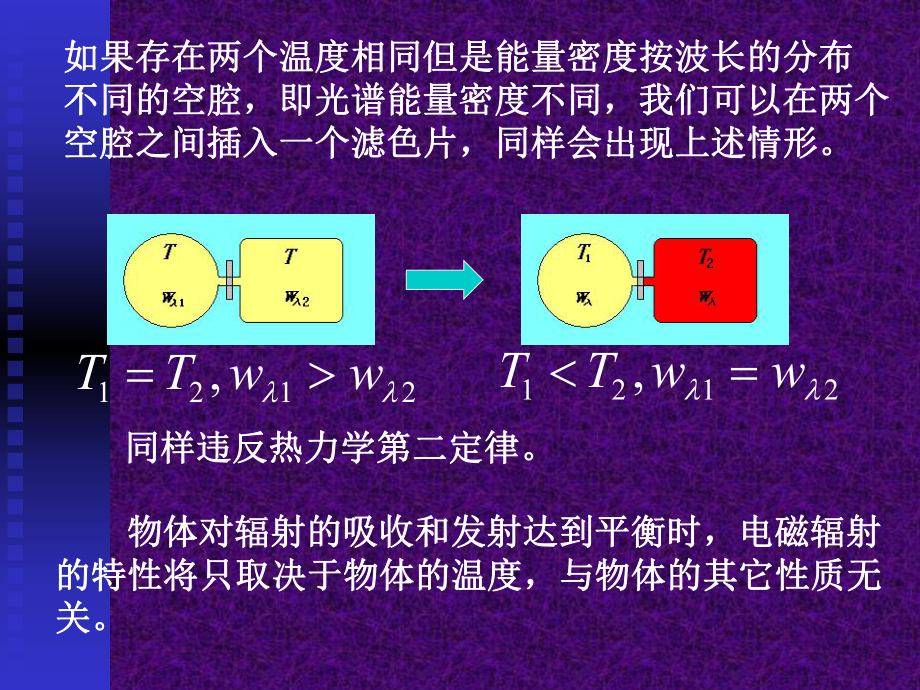
2、荧光光泵浦光泵浦3.2 3.2 理想黑体理想黑体 一、空腔的热平衡辐射一、空腔的热平衡辐射空腔辐射：空腔内的辐射场和腔壁达到热平衡时，具空腔辐射：空腔内的辐射场和腔壁达到热平衡时，具有共同的温度。空腔辐射的能量密度和能量密度按波有共同的温度。空腔辐射的能量密度和能量密度按波长的分布只可能是温度的函数。长的分布只可能是温度的函数。 设想存在两个温度相同但能量密度不同的空腔，设想存在两个温度相同但能量密度不同的空腔，我们可以使之发生热接触（如图所示）：我们可以使之发生热接触（如图所示）：2121,wwTT2121,wwTT这将违反热力学第二定律。这将违反热力学第二定律。如果存在两个温度相同但是能量

3、密度按波长的分布如果存在两个温度相同但是能量密度按波长的分布不同的空腔，即光谱能量密度不同，我们可以在两个不同的空腔，即光谱能量密度不同，我们可以在两个空腔之间插入一个滤色片，同样会出现上述情形。空腔之间插入一个滤色片，同样会出现上述情形。 物体对辐射的吸收和发射达到平衡时，电磁辐射物体对辐射的吸收和发射达到平衡时，电磁辐射的特性将只取决于物体的温度，与物体的其它性质无的特性将只取决于物体的温度，与物体的其它性质无关。关。2121,wwTT2121,wwTT同样违反热力学第二定律。同样违反热力学第二定律。二、基尔霍夫定律二、基尔霍夫定律 设想一物体处于一真空的腔体内，经过一段时间设想一物体处于

4、一真空的腔体内，经过一段时间以后物体与空腔达到热平衡。在热平衡状态下，物体以后物体与空腔达到热平衡。在热平衡状态下，物体发射的辐射功率必然等于它吸收的辐射功率，否则不发射的辐射功率必然等于它吸收的辐射功率，否则不能保持平衡温度不变。能保持平衡温度不变。吸收的辐射功率：吸收的辐射功率：EAPTAEM物体物体A发射的辐射功率发射的辐射功率:MAP 辐照到物体辐照到物体A的辐射功率：的辐射功率：EAPiEAMA在热平衡状态下：在热平衡状态下：EMEMEM TTM TTM,三、密闭空腔辐射为黑体辐射三、密闭空腔辐射为黑体辐射1，理想黑体概念的提出，理想黑体概念的提出2，密闭空腔辐射为黑体辐射，密闭空腔

5、辐射为黑体辐射黑体的辐射出射度等于空腔内的辐射照度。黑体的辐射出射度等于空腔内的辐射照度。设想一黑体处于一密闭的空腔内。设想一黑体处于一密闭的空腔内。bbEM1bbbb空腔内的辐射照度：空腔内的辐射照度：bbME bbME 空腔内的辐射照度是由腔壁的辐照产生的，空腔内的辐射照度是由腔壁的辐照产生的，根据大面源的辐射照度公式：根据大面源的辐射照度公式：MME02sin20bbMM 密闭空腔的光谱辐射出射度等于黑体的光谱辐射密闭空腔的光谱辐射出射度等于黑体的光谱辐射出射度。出射度。 密闭空腔中的辐射就是黑体辐射，与构成空腔的密闭空腔中的辐射就是黑体辐射，与构成空腔的材料无关。材料无关。四、辐射亮度

6、和能量密度的关系四、辐射亮度和能量密度的关系dcdtdA 在均匀的辐射场中取一面积元在均匀的辐射场中取一面积元dA，在立体角，在立体角d内内的辐射功率为：的辐射功率为：dLdAdPcosdt时间内通过时间内通过dA的能量为：的能量为：dtdLdAdQcos 这些能量原来处在截这些能量原来处在截面积为面积为dA，高为，高为 cdtcos 的柱体内，所以的柱体内，所以 方向的方向的辐射能量密度为：辐射能量密度为：cLddAcdtdtdLdAdVdQdwcoscos辐射场的辐射包含所有方向，因此能量密度：辐射场的辐射包含所有方向，因此能量密度：cLcLddww444cwL 4ppcnL 光子辐射亮度

7、光子辐射亮度:如果辐射都是由频率为如果辐射都是由频率为 的光子组成的：的光子组成的：hwnp（单位体积的光子数）（单位体积的光子数）五、黑体为朗伯辐射体五、黑体为朗伯辐射体朗伯辐射体的辐射特性是朗伯辐射体的辐射特性是LM 在处于热平衡的空腔腔壁上任取一点在处于热平衡的空腔腔壁上任取一点x，根据立体，根据立体角投影定理辐射亮度为角投影定理辐射亮度为 L ，通过立体角通过立体角d在在 x 点产生的点产生的辐射照度为：辐射照度为：cos LddEx 点总的照度：点总的照度：2cos dLdEELddLE2020cossin即黑体辐射为朗伯体辐射。即黑体辐射为朗伯体辐射。对黑体辐射：对黑体辐射：LEM

8、如果在空腔表面开一足够小的小孔，近似地认为小孔如果在空腔表面开一足够小的小孔，近似地认为小孔不影响腔体内的辐射分布，小孔的辐射出射度：不影响腔体内的辐射分布，小孔的辐射出射度：LM 即小孔辐射遵守朗伯体的辐射规律，空腔小孔为即小孔辐射遵守朗伯体的辐射规律，空腔小孔为朗伯辐射源。朗伯辐射源。3.3 3.3 普朗克公式普朗克公式一，空腔辐射可能的微观状态数一，空腔辐射可能的微观状态数 根据经典电磁理论，麦克斯韦方程的通解可以表根据经典电磁理论，麦克斯韦方程的通解可以表示为一系列单色平面波的叠加。而单色平面波在有一示为一系列单色平面波的叠加。而单色平面波在有一定边界条件限制下，只能以驻波的形式存在。

9、由此可定边界条件限制下，只能以驻波的形式存在。由此可以得到空腔辐射可能存在的电磁波的模式数。以得到空腔辐射可能存在的电磁波的模式数。现在我们把空腔内的辐射场看成光子气体。现在我们把空腔内的辐射场看成光子气体。对于一维的自由粒子在对于一维的自由粒子在 空间空间所占的相体积的大小（相格）：所占的相体积的大小（相格）：hpqqpoLdph3hdpdpVdpzyx三维自由粒子在三维自由粒子在空间体积空间体积 内的量子态数：内的量子态数：zyxdpdpVdp采用球极坐标：采用球极坐标：sinsinppycossinppxcosppzxpyppdpdpcospdzp动量空间体积元：动量空间体积元：ddpd

10、p sin2hLdpLdp在在空间体积空间体积 内，粒子可能的量子态数：内，粒子可能的量子态数：32sinhddpdVpdddppp动量大小在动量大小在 范围内范围内动量方向在动量方向在在空间体积在空间体积 V 内内自由粒子自由粒子可能的状态数：可能的状态数：范围内范围内dpphV23420032sin ddhdpVpdppp动量大小在动量大小在 范围内范围内在空间体积在空间体积 V 内内自由粒子自由粒子可能的状态数：可能的状态数： 光子的自旋量子数为光子的自旋量子数为1 1，在动量方向上的投影，在动量方向上的投影有两个可能值：有两个可能值：dpphV238（或经典理论的振动自由度数）（或经典

11、理论的振动自由度数）dppp动量大小在动量大小在 范围内范围内在空间体积在空间体积 V 内内光子的光子的量子态数：量子态数：光子的量子态数为：光子的量子态数为：在体积为在体积为 的空腔内的空腔内 V在在 的频率范围内的频率范围内ddchhV32338dcVvgd328hvcp 一个光子的能量一个光子的能量E实验曲线实验曲线维恩公式维恩公式二，维恩的黑体辐射公式二，维恩的黑体辐射公式 维恩从经典热力学的思想出发，假设黑体辐射是维恩从经典热力学的思想出发，假设黑体辐射是由一些服从麦克斯韦速率分布的分子发射出来的：由一些服从麦克斯韦速率分布的分子发射出来的： TCeCE251kTecVE332维恩的

12、公式只在高频（短波长）端和实验结果相符。维恩的公式只在高频（短波长）端和实验结果相符。三，瑞利金斯的黑体辐射公式三，瑞利金斯的黑体辐射公式 根据经典理论的能量均分定理，一个谐振子的能量根据经典理论的能量均分定理，一个谐振子的能量包含两个平方项，每个平方项的平均能量为包含两个平方项，每个平方项的平均能量为: :TKB21cdcd2dVTKdEB48瑞利金斯公式瑞利金斯公式dcVvTKdvEBv328辐射场的总能量：辐射场的总能量：在在 的频率范围内，可能的驻波模式数：的频率范围内，可能的驻波模式数：ddcVvgdv328E瑞利金斯公式瑞利金斯公式的理论曲线。的理论曲线。实验曲线实验曲线维恩公式维

13、恩公式四，普朗克公式的推导四，普朗克公式的推导量子统计：光子是玻色子，遵从玻色分布量子统计：光子是玻色子，遵从玻色分布 1leall11seaflls一个量子态上的平均光子数：一个量子态上的平均光子数：空腔平衡辐射光子数不守恒，空腔平衡辐射光子数不守恒，0kT（平衡状态下光子气体的化学势为零）（平衡状态下光子气体的化学势为零）TKB1hvs11TKhvsBef光子的量子态数为：光子的量子态数为：在体积为在体积为 的空腔内的空腔内 V在在 的频率范围内的频率范围内ddcVvgd328在在 的频率范围内，辐射场的总能量：的频率范围内，辐射场的总能量：dhvedcVvdvETKhB11832dveV

14、chvdvETKhB11833在在 的频率范围内，单位体积内的辐射能：的频率范围内，单位体积内的辐射能：ddvechvdwTKhB11833 ：单位体积、单位频率间隔内的辐射能，也就是：单位体积、单位频率间隔内的辐射能，也就是辐射场的光谱能量密度。辐射场的光谱能量密度。w11833TKhBechvw以频率为变量以频率为变量的普朗克公式的普朗克公式cdcd21185TKhcBehcw以波长为变量以波长为变量的普朗克公式的普朗克公式 ：单位体积、单位波长间隔内的辐射能，也是辐：单位体积、单位波长间隔内的辐射能，也是辐射场的光谱能量密度。射场的光谱能量密度。w五，普朗克辐射定律五，普朗克辐射定律4c

15、wL 根据辐射亮度和能量密度的关系：根据辐射亮度和能量密度的关系：黑体的辐射出射度：黑体的辐射出射度：4cwLMbb11252TKhcbbBehcM黑体辐射光谱分布黑体辐射光谱分布的普朗克公式的普朗克公式即普朗克辐射定律即普朗克辐射定律普朗克公式初始形式（也是使用比较便捷的形式）：普朗克公式初始形式（也是使用比较便捷的形式）：11251TCbbeCM11251TCbbeCM24821107415. 32mmWhcCKmKhcCB42104388. 1C2 第二辐射常数第二辐射常数 c 真空光速真空光速C1 第一辐射常数第一辐射常数h 普朗克常数普朗克常数KB 波尔兹曼常数波尔兹曼常数六，黑体的

16、辐射特性六，黑体的辐射特性黑体的光谱辐射出射度曲线的说明：黑体的光谱辐射出射度曲线的说明：1、 Mbb随波长连续变化，一个温度对应固定一条曲线，随波长连续变化，一个温度对应固定一条曲线，并只有一个极大值。（一旦温度确定，则并只有一个极大值。（一旦温度确定，则Mbb在某波长在某波长处为一的固定值）；处为一的固定值）；2、温度越高，、温度越高， Mbb越大。全辐射出射度越大。全辐射出射度M越大，越大，(M是曲线下方面积）；是曲线下方面积）；4、随着温度、随着温度T的升高，的升高， Mbb的峰值波长向短波方向移的峰值波长向短波方向移动。温度升高，短波比例增加。（温度动。温度升高，短波比例增加。（温度

17、T继续升高就进继续升高就进入可见光区）；入可见光区）；3、每条曲线互不相交，温度越高，所有波长的、每条曲线互不相交，温度越高，所有波长的Mbb也也越大；越大；5、黑体的辐射特性只与其温度有关，与物体其它参数、黑体的辐射特性只与其温度有关，与物体其它参数无关；无关；6、黑体辐射亮度与观察角度无关。、黑体辐射亮度与观察角度无关。七，普朗克公式在极限条件下的近似七，普朗克公式在极限条件下的近似普朗克公式：普朗克公式：11251TCbbeCM（1）当）当 时，时，即，即，12TCTKhcTKhBB,仅适用于黑体辐射的短波部分。仅适用于黑体辐射的短波部分。 此时对应短波或低温情形，普朗克公式中的指数此时

18、对应短波或低温情形，普朗克公式中的指数项远大于项远大于1，故可以把分母中的，故可以把分母中的1忽略，这时普朗克公忽略，这时普朗克公式变为式变为:TCbbeCM251维恩公式维恩公式（2）当）当 时时12TC即，即，TKhcTKhBB, 此时对应波长或高温情形，可将普朗克公式中此时对应波长或高温情形，可将普朗克公式中的指数项展成级数，并取前两项：的指数项展成级数，并取前两项：TCeTC212421TCCMbb 仅适用于黑体辐射的长波部分。仅适用于黑体辐射的长波部分。瑞利瑞利金斯公式金斯公式两种近似式在不同两种近似式在不同T值的计算误差值的计算误差八、不同变量下的普朗克公式八、不同变量下的普朗克公

19、式11833TKhBechvw1 1、以频率为变量的普朗克公式、以频率为变量的普朗克公式根据辐射亮度与能量密度之间的关系：根据辐射亮度与能量密度之间的关系：4cwLv11223TKhvbbBechvLM2 2、以波长为变量的普朗克公式、以波长为变量的普朗克公式11252TKhcbbBehcMdwdcwdvw2cdcd2当初我们是根据下述关系由当初我们是根据下述关系由 得到得到 的：的：wwvcddvMMbbbb2dvMdMbbbb也就是说：也就是说：vMMbbbb因此以波长和频率为变量的辐射出射度有以下关系：因此以波长和频率为变量的辐射出射度有以下关系：3、用圆频率表示的普朗克公式、用圆频率表

20、示的普朗克公式cvc222dcd11252TKhcbbBehcM11822332TKbbbbBechcMM114223TKbbBecMdMdcMdMbbbbbb2222cMMbbbbbbbbMM4、用归一化变量表示普朗克公式、用归一化变量表示普朗克公式令令归一化变量归一化变量：TKTKhcTKhvxBBBTxKhcBbbxbbMxMTKxhcMMBbbxbb21233344xBxbbexchTKMxMMvMMxbbbbbbbb总结：总结：5、用光子数表示的普朗克公式、用光子数表示的普朗克公式一个波长为一个波长为 的光子能量为：的光子能量为：hch11252TKhcbbBehcM 单位时间从单位

21、面积向半球空间辐射波长为单位时间从单位面积向半球空间辐射波长为的单位的单位波长间隔内辐射能量：波长间隔内辐射能量：单位时间从单位面积辐射波长为单位时间从单位面积辐射波长为的光子数：的光子数：hcMMbbbbp1124TKhcbbpBecM11241TCbbpeCMcC21 根据根据 ，还可以算出以频率为变，还可以算出以频率为变量的光子光谱辐射出射度。量的光子光谱辐射出射度。vMMbbpbbpvMMbbppvbb11113212412TKhvTCBecvCvcevcCcC2111222TKhvpvbbBecvM3.43.4、维恩位移定律、维恩位移定律 Mbb随波长连续变随波长连续变化，某一温度对

22、应固定化，某一温度对应固定一条曲线，并只有一个一条曲线，并只有一个极大值。极大值。 随着温度随着温度T的升高，的升高， Mbb的峰值波长向短波的峰值波长向短波方向移动。温度升高，方向移动。温度升高，短波比例增加。短波比例增加。 维恩位移定律反映维恩位移定律反映了了Mbb的峰值波长位置的峰值波长位置随温度变化的这种关系。随温度变化的这种关系。普朗克公式：普朗克公式：11251TCbbeCM在黑体光谱辐射出射度的峰值处：在黑体光谱辐射出射度的峰值处：0bbMTCx2令：令：155251xbbexCTCM015xexx0115254xxxeexex一、维恩位移定律的推导一、维恩位移定律的推导0 xx

23、MMbbbb0 xMbb方程的解：方程的解： x = 4.9651即：即：9651.42TCxm维恩常数：维恩常数：KmTbm8.2897维恩位移定律维恩位移定律:Tbm 其中其中 是表示在温度是表示在温度 T 时黑体光谱辐射出射度时黑体光谱辐射出射度 的峰值的峰值 对应的波长对应的波长 ，通常写为：，通常写为： mmaxbbmMmTbmxxxee15254115xxxeexex二、黑体光谱辐射出射度的峰值二、黑体光谱辐射出射度的峰值TMMbbbb,当当 时：时：m TMMbbbbmm将将 代入代入Tbm11251TCbbeCM5515111122TebCeCMbCTCmbbmm51TbMbb

24、mb1 = 1.286210-11 （W/m2mK5）51TbMbbm维恩最大发射本领定律维恩最大发射本领定律维恩最大发射本领定律表明：维恩最大发射本领定律表明：1、只要温度、只要温度 T 确定，最大发射本领确定，最大发射本领 及相应及相应 波长波长 也确定。也确定。bbmMm2、 的数值和绝对温度的五次方成正比。的数值和绝对温度的五次方成正比。bbmM3、由于、由于 的峰值随温度迅速升高，整个的峰值随温度迅速升高，整个 曲曲 线随之迅速提高，下方面积增大，即全辐射出射线随之迅速提高，下方面积增大，即全辐射出射 度也相应增大。度也相应增大。bbMbbM三、光子辐射量的维恩位移定律三、光子辐射量

25、的维恩位移定律用光子数表示的普朗克公式：用光子数表示的普朗克公式：11241TCbbpeCMcC21TCx2令：令：144241xbbpexCTCM0 xMbbp014xexx01142443xxeexex2443114xxeexexxxxee14方程的解：方程的解：9207. 3x即：即：9207.32TCxm光子维恩常数：光子维恩常数：KmTbm7.3669光子辐射量维恩位移定律光子辐射量维恩位移定律:TbmTbmmm注意：注意：mm 光谱光子辐射出射度的峰值波长比光谱辐射出光谱光子辐射出射度的峰值波长比光谱辐射出射度的峰值波长大约长射度的峰值波长大约长25将将 代入代入Tbm11241T

26、CbbpeCM41TbMbbpm光谱光子辐射出射度的峰值：光谱光子辐射出射度的峰值：42111/1101010. 2Kmmsb3.5 3.5 斯蒂芬玻耳兹曼定律斯蒂芬玻耳兹曼定律普朗克公式普朗克公式描述黑体辐射的光谱分布及其与温度的关系。描述黑体辐射的光谱分布及其与温度的关系。维恩位移定律维恩位移定律描述黑体光谱辐射出射度峰值波长与温度的关系。描述黑体光谱辐射出射度峰值波长与温度的关系。描述黑体全辐射出射度与温度的关系。描述黑体全辐射出射度与温度的关系。斯蒂芬玻耳兹曼定律斯蒂芬玻耳兹曼定律 根据普朗克公式，对波长从根据普朗克公式，对波长从 0 0 到到 积分即可得积分即可得到黑体的全辐射出射度

27、。到黑体的全辐射出射度。一、斯蒂芬玻耳兹曼定律的推导一、斯蒂芬玻耳兹曼定律的推导11251TCbbeCMdeCMTCbb051112( 积分限积分限: 0, 则则 x : 0 )TCx2令：令：dxTxCd22dxTxCeCxTCMxbb2205255111dxTxCeCxTCMxbb2205255111dxexCTCx0342411dxexCTCx0342411151403dxexx4421415TCCMbb421415CC4TMbb斯蒂芬斯蒂芬玻耳兹曼定玻耳兹曼定律律8106697. 542/KmW4TMbb斯蒂芬斯蒂芬玻耳兹曼定玻耳兹曼定律律黑体的全辐射出射度与其温度的四次方成正比。黑体

28、的全辐射出射度与其温度的四次方成正比。二、光子数表示的斯蒂芬玻耳兹曼定律二、光子数表示的斯蒂芬玻耳兹曼定律11241TCbbpeCMTCx2令：令：144241xpxbbexCTCMdxTxCexCTCMxpbb220442411dxexCTCx02323114041. 2102dxexx3215321/1105204. 14041. 2KmsCC3TMpbb3TMpbb黑体的光子辐射出射度与其温度的三次方成正比。黑体的光子辐射出射度与其温度的三次方成正比。hcCC112024041. 21mdxexx记232413232132321mTCKKhcTCTmhcCCTmCCMBBpbbTKmCT

29、CTKmCTCMBBpbb4242414242411515TKTTKmTMBBpbb70. 215442411251TCbbeCMbbPTCMeChcN即11251dNN0pbbTCMdehcC即1112041( 积分限积分限: 0, 则则 x : 0 )TCx2令：令：dxTxCd22dxTxCexCThcCNTC2240424112例例习题习题3，3232310232311mhcCTCdxexhcCTCNxTKmCTCmTKCKhcTCNBBB2424123241TKTmTKTNBB70. 21544243.6 3.6 黑体辐射的简易计算黑体辐射的简易计算一、黑体辐射函数一、黑体辐射函数

30、f(T)f (T) : 称为相对光谱辐射出射度函数，表示温度称为相对光谱辐射出射度函数，表示温度 T 下、波长为下、波长为 的辐射出射度的辐射出射度M和该温度下峰值波长和该温度下峰值波长处的辐射出射度处的辐射出射度Mm之比。之比。mMMTf11251TCeCM根据普朗克公式根据普朗克公式以及维恩最大发射本领定律以及维恩最大发射本领定律51TbMm112511TCeTbCTf 如果能够画出如果能够画出 f(T)和和T 的函数关系的曲线，的函数关系的曲线，那么很多关于黑体辐射的计算变得很简便。那么很多关于黑体辐射的计算变得很简便。 怎么利用怎么利用f(T)和和T 的函数关系的曲线来求得的函数关系的

31、曲线来求得任一波长在温度任一波长在温度T下的光谱辐射出射度？下的光谱辐射出射度？ 比如已知黑体温度比如已知黑体温度T,我们可以根据维恩位移定律我们可以根据维恩位移定律算出：算出： Tbm再根据维恩最大发射本领定律算出：再根据维恩最大发射本领定律算出：51TbMm 现在对任意一个波长现在对任意一个波长，从，从f(T) 曲线上查出曲线上查出相应相应f(T) 数值，就可以算出：数值，就可以算出：51TbTfMTfMm 关于关于f(T)，教材有简易的黑体通用曲线，在一些，教材有简易的黑体通用曲线，在一些工具书上可以查到更精确的工具书上可以查到更精确的f(T)函数表。函数表。二、黑体辐射函数二、黑体辐射

32、函数 F(T)00MMTF称为相对辐射出射度函数称为相对辐射出射度函数表示温度表示温度T下、下、0 波段的辐射出射度波段的辐射出射度M 0和该温和该温度下全辐射出射度度下全辐射出射度M 0 之比。之比。 同样我们有简易的黑体通用曲线同样我们有简易的黑体通用曲线F(T)，也可以，也可以查到更精确的查到更精确的F(T)值。值。根据斯蒂芬根据斯蒂芬玻耳兹曼定律我们可以求得：玻耳兹曼定律我们可以求得：40TM 怎么利用怎么利用F(T)来求在某一温度下，任意光谱带的来求在某一温度下，任意光谱带的辐射出射度？辐射出射度？对于波长对于波长2420202TTFMTFM据此可以算出据此可以算出12的辐射出射度：

33、的辐射出射度：122100MMM412TTFTF对于波长对于波长1410101TTFMTFM三、计算举例三、计算举例例例1(1(习题习题6 6）：）：已知黑体温度已知黑体温度 T = 1000K，求：其，求：其峰值波长、光峰值波长、光 谱辐射度峰值、在谱辐射度峰值、在=4m处的光谱辐射处的光谱辐射出射度、出射度、35 m波段的辐射出射度。波段的辐射出射度。2.光谱辐射度峰值光谱辐射度峰值根据维恩最大发射本领定律根据维恩最大发射本领定律mmWTbMm2451151/102862. 11000102862. 11.峰值波长峰值波长根据维恩位移定律根据维恩位移定律mKKmTbm898.2100028

34、98KmKmT4000100048 . 0Tf3.在在=4m处的光谱辐射出射度处的光谱辐射出射度44102862. 180. 0mMTfMmmmWMm244/1003. 14.在在=35m波段内的辐射出射度波段内的辐射出射度43050531000310005TFFMMM427. 063. 0T24/1004. 2mW例例2 2：已知人体的温度已知人体的温度T=310K（假定人体的皮（假定人体的皮肤是黑体），求其辐射特性。肤是黑体），求其辐射特性。1.其峰值波长其峰值波长mTm4 . 931028982898根据维恩位移定律根据维恩位移定律2.全辐射出射度全辐射出射度22484/102 . 53

35、101067. 5mWTM斯蒂芬斯蒂芬玻耳兹曼定玻耳兹曼定律律3.处于紫外区，波长（处于紫外区，波长（00.4m）的辐射出射度）的辐射出射度KmKmT1243104.0?TF0TF04 . 00MTFMm人体不发射紫外线人体不发射紫外线4、可见光区，波长在（、可见光区，波长在（0.40.75m）的辐射出射度）的辐射出射度KmKmT23331075.00TF075. 00mM075. 040mM人体基本上不发射可见光人体基本上不发射可见光5、处于红外区，波长（、处于红外区，波长（0.75）的辐射出射度）的辐射出射度2275. 0/102 . 5mWMMm例3 太阳的温度太阳的温度T=6000K并

36、认为是黑体，求其并认为是黑体，求其辐射特性。辐射特性。1.峰值波长峰值波长mKKmTbm48.0600028982、全辐射出射度、全辐射出射度27484/103 . 760001067. 5mWTM3、紫外区的辐射出射度、紫外区的辐射出射度mM4 . 00KmKmT240060004.014.0TF274 . 00/1002. 114. 0mWMMm4、可见光区的辐射出射度、可见光区的辐射出射度KmKmT4500600075.056.0TFMMMm42. 014. 056. 075. 040775. 040103 . 742. 0mM27/1007. 3mW5、红外区的辐射出射度、红外区的辐射

37、出射度2775. 0/1021. 344. 056. 01mWMMMm3.7 3.7 辐射效率和辐射对比度辐射效率和辐射对比度一、辐射效率一、辐射效率 在实际工作中，探测器搜寻的往往是特定波长的在实际工作中，探测器搜寻的往往是特定波长的信号，也就是目标源的工作信标。所以我们希望这个信号，也就是目标源的工作信标。所以我们希望这个工作波长的光谱辐射出射度有相对较高的值。工作波长的光谱辐射出射度有相对较高的值。定义波长定义波长 的光谱辐射效率：的光谱辐射效率：MM11251TCeCM4TM4511112TeCTCTCx2令：令：xCT21114421424451xxexCCCxeC 对于特定波长对于

38、特定波长 e ，我们可以通过调节温度使其光，我们可以通过调节温度使其光谱辐射效率达到最大值，这时：谱辐射效率达到最大值，这时：0T014xexT243114xxxeexex41xxexe9207. 3xKmTmm8.2897注意：不同于维恩位移定律注意：不同于维恩位移定律eT工程最大值对应的温度。工程最大值对应的温度。mT物理最大值对应的温度。物理最大值对应的温度。 也就是说：黑体辐射对特定波长也就是说：黑体辐射对特定波长 ， 它的最大光谱它的最大光谱辐射效率并不是出现在以它为光谱辐射出射度峰值位置的辐射效率并不是出现在以它为光谱辐射出射度峰值位置的温度温度 Tm ，而是温度比，而是温度比Tm

39、更高的更高的 Te。eKmTee7.36699207.32eeTC对一定波长对一定波长，最大光谱效率的温度是，最大光谱效率的温度是Te， Te Tm对一定温度对一定温度T，最大光谱效率的波长是，最大光谱效率的波长是m二、辐射对比度二、辐射对比度目标辐射和背景辐射目标辐射和背景辐射辐射对比度：目标和背景辐射出射度之差与背景辐射对比度：目标和背景辐射出射度之差与背景 辐射出射度之比。辐射出射度之比。BBTMMMCTMBM目标辐射出射度目标辐射出射度背景辐射出射度背景辐射出射度一般测量总是局限在一个波带范围内，此时：一般测量总是局限在一个波带范围内，此时：dTMMTT)(21dTMMBB)(21BT

40、MMM21 dTMTMMBT2121TdTMM2121BTTTTdTMTM2121TM因此，衡量辐射对比度可以有两个参量作为选择测因此，衡量辐射对比度可以有两个参量作为选择测量波段的依据：量波段的依据：光谱辐射出射度随温度的变化率；光谱辐射出射度随温度的变化率；TM21光谱带辐射出射度随温度的变化率。光谱带辐射出射度随温度的变化率。我们可以通过选择测量波长使得我们可以通过选择测量波长使得 达到极大值。达到极大值。TM11251TCeCM22251122TCeeCTMTCTCTC2测量通常在常温下进行，所以测量通常在常温下进行，所以222251112TCMTCeCTMTC1122621TCeTC

41、CTMTCx2令：令：TxC2165241xexCTCTM00TMxTM即265116xxxeexex61xxexe9694. 5xKmxCTc24112TTMTKmc2411mmc832. 028982411常温下（常温下（T=300K）mc8TM21在在814m波段有最大值。波段有最大值。3.8 3.8 发射率和实际物体的辐射发射率和实际物体的辐射 黑体是理想化的物理模型，实际物体的辐射本领黑体是理想化的物理模型，实际物体的辐射本领总是小于理想黑体，衡量辐射体辐射本领的物理量是总是小于理想黑体，衡量辐射体辐射本领的物理量是发射率。发射率。 辐射体的发射率是指在一定温度下，物体的辐射辐射体的

42、发射率是指在一定温度下，物体的辐射量与同温度黑体的相应辐射量的比值。量与同温度黑体的相应辐射量的比值。一、各种发射率的定义一、各种发射率的定义1、半球发射率（比辐射率）、半球发射率（比辐射率） 辐射体的辐射出射度与同温度下的黑体的辐射出辐射体的辐射出射度与同温度下的黑体的辐射出射度的比值射度的比值: TMTMbbh半球光谱发射率：半球光谱发射率： TMTMTbbh根据热平衡时辐射和吸收的关系：根据热平衡时辐射和吸收的关系：bbbbbbMMM TTh TTh同理同理 任何物体的半球光谱发射率与该物体在同温度下的任何物体的半球光谱发射率与该物体在同温度下的光谱吸收率相等；物体的半球全发射率与该物体

43、在同温光谱吸收率相等；物体的半球全发射率与该物体在同温度下的全吸收率相等。度下的全吸收率相等。 这是基尔霍夫定律的表示形式之一：物体的吸收本这是基尔霍夫定律的表示形式之一：物体的吸收本领越强，其发射本领也越强。领越强，其发射本领也越强。2.2.方向发射率（角比辐射率）方向发射率（角比辐射率） 方向发射率反应物体向着某一方向发射辐射的本方向发射率反应物体向着某一方向发射辐射的本领，所以也叫定向发射本领领，所以也叫定向发射本领: : TLTLTbb,是与物体表面法线方向的夹角是与物体表面法线方向的夹角 TLTLTbb,方向光谱发射率：方向光谱发射率：法向发射率和法向光谱发射率：法向发射率和法向光谱

44、发射率：0n0n二、朗伯辐射体的发射率二、朗伯辐射体的发射率对于朗伯辐射体：对于朗伯辐射体： 辐射亮度是和方向无关的常数；辐射亮度是和方向无关的常数； LMLM 朗伯体的半球发射率：朗伯体的半球发射率： TMTMbbh朗伯体的半球光谱发射率：朗伯体的半球光谱发射率： TMTMTbbh朗伯体的方向发射率：朗伯体的方向发射率： hbbbbMMLL朗伯体的方向光谱发射率：朗伯体的方向光谱发射率： hbbbbMMLL朗伯体的法向发射率：朗伯体的法向发射率： hn朗伯体的法向光谱发射率：朗伯体的法向光谱发射率： hn朗伯辐射体的三种发射率朗伯辐射体的三种发射率n n，( () )和和h h彼此相等彼此相

45、等朗伯体的三种光谱发射率也彼此相等朗伯体的三种光谱发射率也彼此相等三、物体发射率的一般变化规律三、物体发射率的一般变化规律（1 1）对于朗伯辐射体：对于朗伯辐射体： 1nnh大多数材料在角度不太大时接近朗伯体。大多数材料在角度不太大时接近朗伯体。电绝缘体角度小于电绝缘体角度小于70时可以看成朗伯体：时可以看成朗伯体： 11nnh导电体导电体 的范围在的范围在nh33. 105. 1 n当当 50 时，时， 和和 差异较大。差异较大。（2 2）金属的发射率较低，一般小于）金属的发射率较低，一般小于0.10.1；非金属的发射率较高，一般大于非金属的发射率较高，一般大于0.90.9。（3 3）非透明

46、材料的辐射发生在表面几微米内，因）非透明材料的辐射发生在表面几微米内，因 此材料的表面性质将极大的影响发射率。此材料的表面性质将极大的影响发射率。金属的氧化层极大地提高发射率（金属的氧化层极大地提高发射率（0.60.6）；）；抛光的金属表面将降低发射率；抛光的金属表面将降低发射率；材料如果存在涂层，辐射反映的是涂层的性质。材料如果存在涂层，辐射反映的是涂层的性质。（4）温度对发射率的影响：）温度对发射率的影响：金属的发射率随温度升高而上升；金属的发射率随温度升高而上升；非金属的发射率随温度升高而降低。非金属的发射率随温度升高而降低。(5)(5)介质的光谱发射率随波长变化而变化介质的光谱发射率随

47、波长变化而变化 在红外区域，大多数介质的光谱发射率随波长在红外区域，大多数介质的光谱发射率随波长的增加而降低。的增加而降低。四、热辐射体的分类四、热辐射体的分类根据辐射体的光谱发射率来划分热辐射体的分类。根据辐射体的光谱发射率来划分热辐射体的分类。1、黑体、黑体黑体的发射率和光谱发射率均等于黑体的发射率和光谱发射率均等于 1 。普朗克公式普朗克公式描述黑体辐射的光谱分布及其与温度的关系。描述黑体辐射的光谱分布及其与温度的关系。维恩位移定律维恩位移定律描述黑体光谱辐射出射度峰值波长与温度的关系。描述黑体光谱辐射出射度峰值波长与温度的关系。描述黑体全辐射出射度与温度的关系。描述黑体全辐射出射度与温度的关系。斯蒂芬玻耳兹曼定律斯蒂芬玻耳兹曼定律黑体的辐射特性由下列定律描述：黑体的辐射特性由下列定律描述：2 2，灰体，灰体灰体的各发射率和光谱发射率均相等，是小于灰体的各发射率和光谱发射率均相等，是小于 1 的常数。的常数。 hnhnbbgMMbbgMMbbgLLbbgLL因此灰体一定是朗伯体因此灰体一定是朗伯体灰体相当于压缩的黑体，压缩比例是灰体