了的IIR和FIR数字滤波器的分析和设计方法,所设计的滤波ppt课件

1、第六章和第七章分别引见了的IIR和FIR数字滤波器的分析和设计方法，所设计的滤波器根本可以满足各种实际运用。但在实际义务中，运用场所不同，有时对滤波器提出一些特殊要求，这时需求设计一些特殊类型的滤波器。第8章 其它类型的数字滤波器 全通滤波器 梳状滤波器 最小相位系统 格型滤波器8.1 几种特殊的滤波器一全通滤波器 假设滤波器的幅频特性对一切频率均等于常数或1，即 那么该滤波器为全通滤波器。全通滤波器频响可表示为： 信号经过全通滤波器后，幅度谱坚持不变，相位谱随(w)改动，起纯相位滤波作用。第8章 其它类型的数字滤波器|H(ejw)|=1，0 2H(ejw)=ej(w)1、全通滤波器的系统函数

2、普通方式为：第8章 其它类型的数字滤波器00121201212( ),11NN kkkNkkkNNNNNNa zH za zza za zaaa za za z00121201212( ),11NN kkkNkkkNNNNNNa zH za zza za zaaa za za z全通滤波器的系统函数构成的特点： 系数均为实数； 分子、分母多项式的系数一样，陈列顺序相反；211221121( )1Liiiiiza zaH za za z二阶滤波器级联方式：性质：全通滤波器具有全通幅频特性第8章 其它类型的数字滤波器10000()( )( )NNNkkkkNNkkNNkkkkkka za zD z

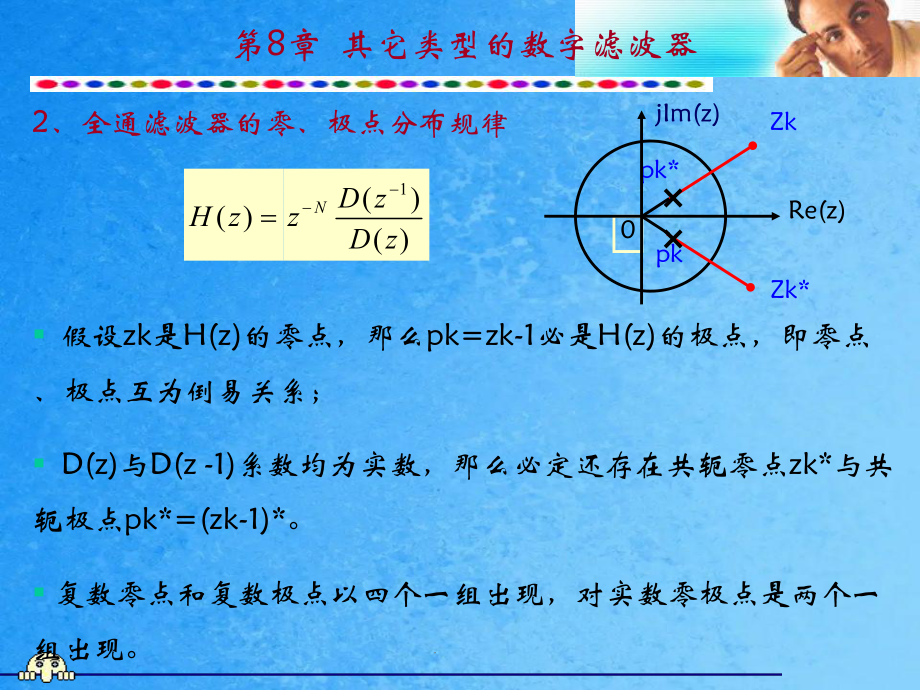
3、H zzzD za za z0( )NkkkD za z系数ak是实数：有1()()()()()1()jjjz ejjjD zD eDeDeH eD e1()()()()()1()jjjz ejjjD zD eD eD eH eD e2、全通滤波器的零、极点分布规律第8章 其它类型的数字滤波器10000()( )( )NNNkkkkNNkkNNkkkkkka za zD zH zzzD za za z10000()( )( )NNNkkkkNNkkNNkkkkkka za zD zH zzzD za za z0Re(z)jIm(z)Zkpkpk*Zk* 假设zk是H(z)的零点，那么pk=zk

4、-1必是H(z)的极点，即零点、极点互为倒易关系； D(z)与D(z -1)系数均为实数，那么必定还存在共轭零点zk*与共轭极点pk*=(zk-1)*。 复数零点和复数极点以四个一组出现，对实数零极点是两个一组出现。假设将零点zk和极点pk*组成一对，将零点zk*与极点pk组成一对，使零、极点呈共轭倒易关系，那么全通滤波器方式可写为：全通滤波器的用途： 是一种纯相位滤波器，常用于相位平衡。第8章 其它类型的数字滤波器111( )1NkkkzzH zz z假设要求设计一个线性相位滤波器： 可以设计一个具有线性相位的FIR滤波器； 可先设计一个满足幅频特点要求的IIR滤波器，再级联一个全通滤波器进

5、展相位校正，使总的相位特性是线性的。第8章 其它类型的数字滤波器二、梳状滤波器假设将滤波器的系统函数 H(z) 中的 z 用 zN 替代，得到H(zN)，那么频响函数 H(ejwN) 是以2/N为周期的，在区间0，2上有N个周期。利用这一性质，可以构造各种梳状滤波器。如N=8时，零点为Zk= e j2k/8，k=0,1,7；极点 其零、极点分布、幅频特性曲线图如下 ,eaPk82j81k=111( )1zH zaz1()1NNNzH zaz例：知 ，0a1，零点为1，极点为a。H(z)表示一高通滤波器。以 ZN 替代 H(z)的 Z，得到：第8章 其它类型的数字滤波器01Re(z)jIm(z)

6、81aIm( z)Re( z)1(a)N1零点在单位圆上极点在半径为 的圆上N10N2 N4N6N8 N10(b)Hk(e j)梳状滤波器的零极点分布和幅频呼应特性(N=8) kN2 =梳状滤波器的作用：可以滤除输入信号中 ，k=0,1,N-1的频率分量。可用于消除电网谐波干扰，彩色电视接纳机中用于亮色分别和色分别。第8章 其它类型的数字滤波器三、最小相位系统时域离散线性非时变系统H(z)因果稳定的条件： 一切的极点必需在单位圆内，但零点可以在z平面任何位置；最小相位系统Hmin(z)：一切零点位于单位圆内 ；最大相位系统Hmax(z)：一切零点位于单位圆(|Z|=1)外 ；混合相位系统： 单

7、位圆内、外都有零点；对于因果稳定系统H(z)第8章 其它类型的数字滤波器最小相位系统特点：1任何一个非最小相位系统H(z)均可由一个最小相位系统Hmin(z)和一个全通系统Hap(z)级联而成。即：H(z)=Hmin(z) Hap(z)。推论：将系统位于单位圆外的零(极)点Zk用其镜像点1/Zk*替代时，不会影响系统幅频呼应特性，并确保系统因果稳定。2在幅频呼应特性一样的一切因果稳定系统中，最小相位系统的相位延迟最小。3最小相位系统保证其逆系统存在。 假设H(z)=A(z)/B(z)，那么逆系统：H inv(z) =1/H(z)=B(z)/A(z)。 当H(z)是最小相位系统时，那么1/H(z

8、)才是因果稳定。第8章 其它类型的数字滤波器四、格形滤波器 在数字信号处置中，格型网络在功率谱的估计、语音处置、自顺应滤波，线性预测和逆滤波等方面有着广泛的运用。1、全零点(FIR)格形滤波器设一个M阶的FIR滤波器的系统函数H(z)写成如下方式：( )01( )( )1MMiiiiMiiH zB zbzb z 其中：表示 M 阶 FIR 滤波器的第 i 个系数bM(i)首项系数 b0 =1第8章 其它类型的数字滤波器H(z)对应格形网络构造图为：x(n)y(n)e0e1e2eM-1eMr0r1r2rM-1rMZ -1Z -1Z -1Z -1k1k1k2k2kM-1kM-1kMkM全零点格形滤

9、波器网络构造 该构造由 M 个格形网络单元级联而成。em-1rm-1rmZ -1kmkmemem(n)=em-1(n)+rm-1(n-1)kmrm(n)=em-1(n) km +rm-1(n-1)e0(n)=r0(n)=x(n)y(n)=eM(n) 第8章 其它类型的数字滤波器设Bm(z)、Jm(z)分别表示由输入端x(n)至第m个根本单元上、下输出端em(n)、 rm(n)对应的系统函数。即：( )010( )( )/( )1,1,2,( )( )/( ),1,2,miimmmimmBzEzEzb zmMJzRzR z mM ( )010( )( )/( )1,1,2,( )( )/( ),

10、1,2,miimmmimmBzEzEzb zmMJzRzR z mM ( )010( )( )/( )1,1,2,( )( )/( ),1,2,miimmmimmBzEzEzb zmMJzRzR z mM H(z) 系数 与格形构造网络系数 ki 的递推关系为： bM (i) 详细的递推步骤为： (1) kM=bM；(M)(2)由 求得 ，得到( )( )()11()( )()( )1121mmiim immmmmmmim iimmmmmbkbbk bkbbk bbkbM1(i)kM1=bM1；(M1)(3)反复步骤2，分别求出kM，kM-1，k1。第8章 其它类型的数字滤波器例: FIR滤波

11、器由如下差分方程给定：1351( )( )(1)(2)(3)2483y nx nx nx nx n 解 : 对差分方程两边进展Z变换的H(z)=B3(z)： 求其格型构造系数， 并画出格型构造图。3( )123331(1)(2)(3)333(3)331351( )( )1124831351,248313iiH zB zbzzzbbbkb z -i3( )123331(1)(2)(3)333(3)331351( )( )1124831351,248313iiH zB zbzzzbbbkb 3( )123331(1)(2)(3)333(3)331351( )( )1124831351,248313

12、iiH zB zbzzzbbbkb 3( )123331(1)(2)(3)333(3)331351( )( )1124831351,248313iiH zB zbzzzbbbkb 3( )123331(1)(2)(3)333(3)331351( )( )1124831351,248313iiH zB zbzzzbbbkb 3( )123331(1)(2)(3)333(3)331351( )( )1124831351,248313iiH zB zbzzzbbbkb (1)(2)(1)333223(2)(1)(2)333223(2)22(1)(1)(1)222122(1)1113532424818

13、91121211414bk bbkbk bbkkbbk bbkkb(1)(2)(1)33 3223(2)(1)(2)33 3223(2)22(1)(1)(1)222122(1)111353242481891121211414bk bbkbk bbkkbbk bbkkb(1)(2)(1)333223(2)(1)(2)333223(2)22(1)(1)(1)222122(1)111353242481891121211414bk bbkbk bbkkbbk bbkkb(1)(2)(1)33 3223(2)(1)(2)33 3223(2)22(1)(1)(1)222122(1)111353242481

14、891121211414bk bbkbk bbkkbbk bbkkb第8章 其它类型的数字滤波器1/4z11/4z11/21/21/31/3z1y(n)x(n)第8章 其它类型的数字滤波器2、全极点(IIR)格形滤波器设M阶全极点IIR 滤波器的系统函数为：( )111( )( )1MiiMiH zA zaz与全零点系统函数比较可知，IIR系统的H(z)与FIR的B(z)互为逆系统，因此，可按求逆准那么，求其格形构造图。( )01( )( )1MMiiiiMiiH zB zbzb z ( )01( )( )1MMiiiiMiiH zB zbzb z 系统求逆步骤为： 将输入至输出的无延时通路全部反向，并将该通路的常数值支路增益变为其相应的倒数，(1的倒数仍为1)； 将指向这条新通路各节点的