2421点与圆的位置关系

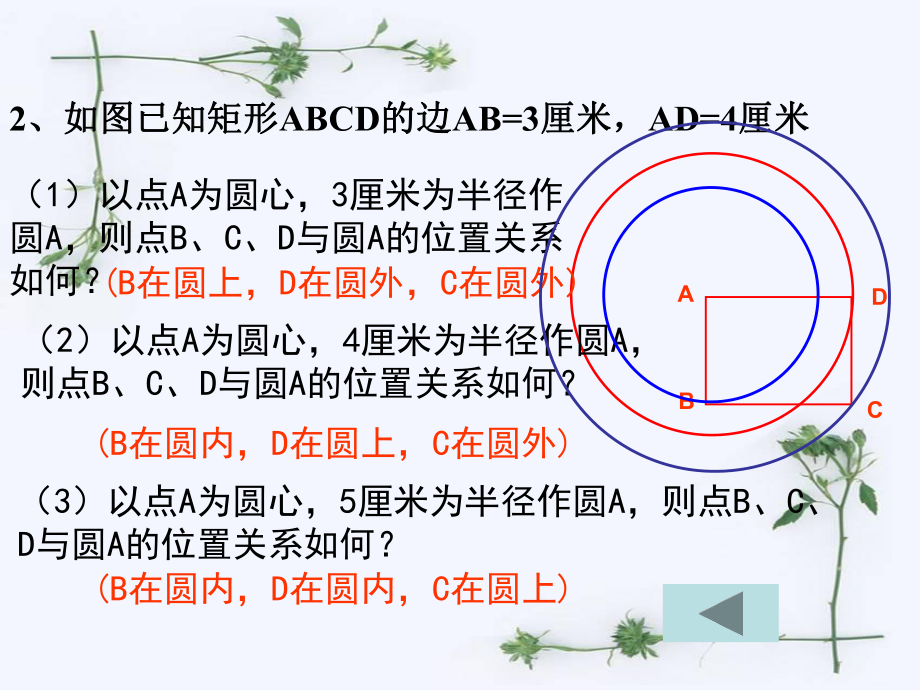
1、24.2.124.2.1点和圆的位置关系点和圆的位置关系济水一中数学组张雪平探究探究：1、请你在练习本上画一个圆，然后任、请你在练习本上画一个圆，然后任意作一些点，观察这些点和圆的位置关系。意作一些点，观察这些点和圆的位置关系。2、量一量这些点到圆心的距离。你发现了什、量一量这些点到圆心的距离。你发现了什么？么？学生自学完成：学生自学完成：设设 O的半径为的半径为r，点到圆心的距离为，点到圆心的距离为d。则。则点和圆的位置关系点在圆内点在圆内dr点在圆上点在圆上点在圆外点在圆外drdr学生自学口答：学生自学口答：1、已知圆的半径等于、已知圆的半径等于5厘米，点到圆心厘米，点到圆心的距离是：（的

2、距离是：（1）8厘米厘米 （ 2）4厘米厘米 （ 3）5厘米。厘米。请你分别说出点与圆的位置关系。请你分别说出点与圆的位置关系。2、如图已知矩形、如图已知矩形ABCD的边的边AB=3厘米，厘米，AD=4厘米厘米ADCB（1）以点A为圆心，3厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？ (B在圆上，D在圆外，C在圆外)（2）以点A为圆心，4厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？(B在圆内，D在圆上，C在圆外)（3）以点A为圆心，5厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？(B在圆内，D在圆内，C在圆上)自己动手探究（自己动手探究（1）1、过一个已知点、过一个

3、已知点A如何作圆？如何作圆？2、过点、过点A所作圆的圆心在哪里？半径多大？所作圆的圆心在哪里？半径多大？可以作几个这样的圆？可以作几个这样的圆？探究（探究（2）1、过已知两点、过已知两点A、B如何作圆？如何作圆？2、圆心与、圆心与A、B两点的距离怎样？能用式子表示吗？两点的距离怎样？能用式子表示吗？圆心在哪里？过点圆心在哪里？过点A、B两点的圆有几个？两点的圆有几个？ 探究（探究（3）1、过同一平面内三个点的情况会、过同一平面内三个点的情况会怎样呢？怎样呢？1、不在同一直线上的三点、不在同一直线上的三点A、B、C。定理：过不在同一直线上的三点确定一个圆定理：过不在同一直线上的三点确定一个圆。2

4、、过在同一直线上的三点、过在同一直线上的三点A、B、C可以作几可以作几个圆？个圆？不能作出。不能作出。BACO学生阅读学生阅读92页，完成以下填空：页，完成以下填空：如图：如图： O是是 ABC的的 圆，圆， ABC 是是 O的的 三角形，三角形，O是是 ABC的的 心，它心，它是是 的交点，到的交点，到三角形三角形 的距离相等。的距离相等。 外接外接内接内接外外三角形三边垂直平分线三角形三边垂直平分线三个顶点三个顶点 经过三角形三个顶点可以画一个圆，并且只能经过三角形三个顶点可以画一个圆，并且只能画一个经过三角形三个顶点的圆叫做画一个经过三角形三个顶点的圆叫做三角形的外三角形的外接圆接圆三角

5、形外接圆的圆心叫做这个三角形外接圆的圆心叫做这个三角形的三角形的心心这个三角形叫做这个这个三角形叫做这个圆的内接三角形圆的内接三角形三角形三角形的外心就是三角形三条边的垂直平分线的交点的外心就是三角形三条边的垂直平分线的交点BACO想一想：想一想：锐角三角形、直角三角锐角三角形、直角三角 形、钝角三角形的外心各在形、钝角三角形的外心各在哪里？哪里？BCABAC反馈练习一、判断：一、判断：1、经过三点一定可以作圆。（、经过三点一定可以作圆。（ ）2、三角形的外心就是这个三角形两边垂直平分线的、三角形的外心就是这个三角形两边垂直平分线的交点。（交点。（ ）3、三角形的外心到三边的距离相等。（、三角

6、形的外心到三边的距离相等。（ ）4、经过不在一直线上的四点能作一个圆。（、经过不在一直线上的四点能作一个圆。（ ） 二、填空：二、填空：1、已知、已知 O的半径为的半径为4，OP3.4，则，则P在在 O的的 （ ）。）。2、已知、已知 点点P在在 O的外部，的外部，OP5，那么，那么 O的半径的半径r满足（满足（ ）3、 已知已知 O的半径为的半径为5，M为为ON的中点，当的中点，当OM3时，时，N点与点与 O的位置关系是的位置关系是N在在 O的（的（ ）内部内部0r 5外部外部 三、三、一位考古学家在马王堆汉墓挖掘时，发一位考古学家在马王堆汉墓挖掘时，发现一圆形瓷器碎片，你能帮助这位考古学家

7、画现一圆形瓷器碎片，你能帮助这位考古学家画出这个碎片所在的整圆，以便于进行深入的研出这个碎片所在的整圆，以便于进行深入的研究吗？究吗？学生思考1、过三角形的三个顶点是否都可以作圆？为、过三角形的三个顶点是否都可以作圆？为什么？什么？2、一个三角形的外接圆有几个？一个圆的内、一个三角形的外接圆有几个？一个圆的内接三角形有几个？为什么？接三角形有几个？为什么？3、三角形的外心有什么性质？它一定在三角、三角形的外心有什么性质？它一定在三角形的内部吗？画图说明。形的内部吗？画图说明。自学完成：应用 某一个城市在一块空地新建了三个居某一个城市在一块空地新建了三个居民小区，它们分别为民小区，它们分别为A、B、C，且三个小，且三个小区不在同一直线上，要想规划一所中学，区不在同一直线上，要想规划一所中学，使这所中学到三个小区的距离相等。请问使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置？你怎么确