自动控制原理实验报告

1、-实验报告课程名称：自动控制原理实验工程：典型环节的时域相应实验地点：自动控制实验室实验日期： 2021 年 3 月 22 日指导教师：乔学工实验一典型环节的时域特性一、实验目的1.熟悉并掌握TDN-ACC+设备的使用方法及各典型环节模拟电路的构成方法。2.熟悉各种典型环节的理想阶跃相应曲线和实际阶跃响应曲线。比照差异，分析原因。3.了解参数变化对典型环节动态特性的影响。二、实验设备 PC机一台，TD-ACC+(或TD-ACS)实验系统一套。三、实验原理及容下面列出各典型环节的方框图、传递函数、模拟电路图、阶跃响应，实验前应熟悉了解。1 比例环节 (P)(1)方框图(2)传递函数：(3)阶跃响

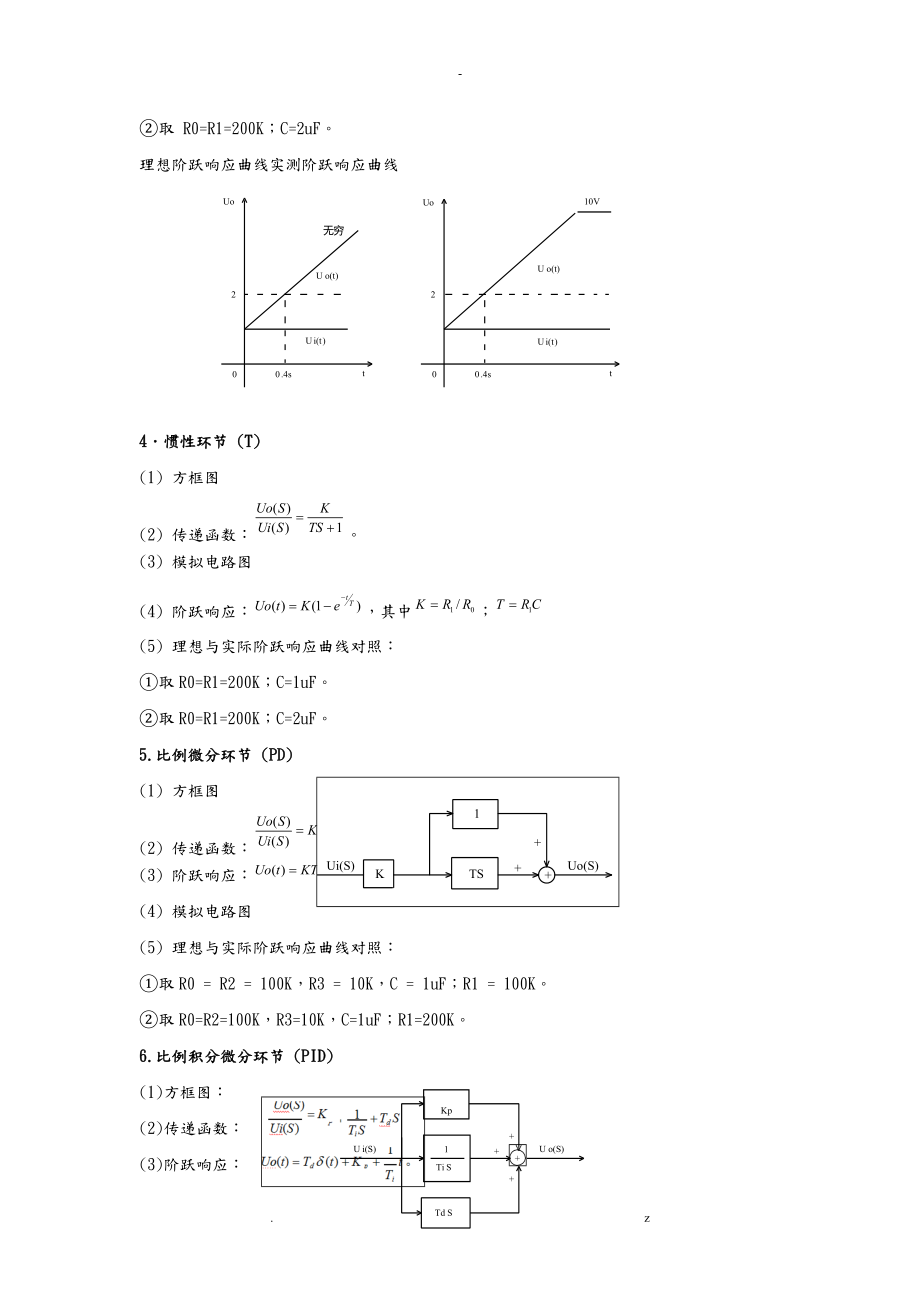
2、应：其中(4)模拟电路图：(5)理想与实际阶跃响应对照曲线：取R0 = 200K；R1 = 100K。取R0 = 200K；R1 = 200K。2积分环节 (I)(1)方框图(2)传递函数：(3)阶跃响应：其中(4)模拟电路图(5) 理想与实际阶跃响应曲线对照：取R0 = 200K；C = 1uF。取R0 = 200K；C = 2uF。3比例积分环节 (PI)(1)方框图：K1TS+U i(S)+U o(S)+(2)传递函数：(3)阶跃响应：(4)模拟电路图：(5)理想与实际阶跃响应曲线对照：取 R0 = R1 = 200K；C = 1uF。理想阶跃响应曲线实测阶跃响应曲线Uo 10VU o(

3、t)21U i(t )00 .2stUo 无穷U o(t)21U i(t )00 .2st取 R0=R1=200K；C=2uF。理想阶跃响应曲线实测阶跃响应曲线Uo 无穷U o(t)21U i(t )00 .4stUo 10VU o(t)21U i(t )00 .4st4惯性环节 (T)(1) 方框图(2) 传递函数：。(3) 模拟电路图(4) 阶跃响应：，其中；(5) 理想与实际阶跃响应曲线对照：取R0=R1=200K；C=1uF。取R0=R1=200K；C=2uF。5.比例微分环节 (PD)(1) 方框图(2) 传递函数：(3) 阶跃响应：。(4) 模拟电路图(5) 理想与实际阶跃响应曲线

4、对照：取R0 = R2 = 100K，R3 = 10K，C = 1uF；R1 = 100K。取R0=R2=100K，R3=10K，C=1uF；R1=200K。6.比例积分微分环节 (PID)Kp +U i(S)1Ti S+U o(S)+Td S(1)方框图：(2)传递函数：(3)阶跃响应：(4)模拟电路图：(5)理想与实际阶跃响应曲线对照：取 R2 = R3 = 10K，R0 = 100K，C1 = C2 = 1uF；R1 = 100K。取 R2 = R3 = 10K，R0 = 100K，C1 = C2 = 1uF；R1 = 200K。四、实验步骤及结果波形1.按所列举的比例环节的模拟电路图将

5、线接好。检查无误后开启设备电源。2.将信号源单元的“ST端插针与“S端插针用“短路块短接。由于每个运放单元均设置了锁零场效应管，所以运放具有锁零功能。将开关分别设在“方波档和“500ms12s档，调节调幅和调频电位器，使得“OUT端输出的方波幅值为1V，周期为10s左右。3.将2中的方波信号加至环节的输入端Ui，用示波器的“CH1和“CH2表笔分别监测模拟电路的输入Ui端和输出U0端，观测输出端的实际响应曲线U0(t)，记录实验波形及结果。4.改变几组参数，重新观测结果。5.用同样的方法分别搭接积分环节、比例积分环节、比例微分环节、惯性环节和比例积分微分环节的模拟电路图。观测这些环节对阶跃信号

6、的实际响应曲线，分别记录实验波形的结果。6.各典型环节不同参数下的阶跃响应曲线的实验结果：1.比例环节取R0=200K；R1=100K。取R0=200K；R1=200K。2.积分环节取R0=200K；C=1uF。取R0=200K；C=2uF。3.比例积分环节取R0=R1=200K；C=1uF。取R0=R1=200K；C=2uF。4.惯性环节取R0=R1=200K；C=1uF。取R0=R1=200K；C=2uF。5.比例微分环节取R0=R2=200K，R3=10K，C=1uF，R1=100K。取R0=R2=200K，R3=10K，C=1uF，R1=200K。6.比例积分微分环节取R2=R3=20

7、0K，R0=10K，C1=C2=1uF，R1=100K。取R2=R3=200K，R0=10K，C1=C2=1uF，R1=200K实验报告课程名称：自动控制原理实验工程： 典型二阶系统的时域分析 实验地点：自动控制实验室实验日期： 2021 年 3 月 22 日指导教师：乔学工实验二典型二阶系统的时域特性一、实验目的1研究二阶系统的特征参量 (、n) 对过渡过程的影响。2研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。3熟悉 Routh 判据，用 Routh 判据对三阶系统进展稳定性分析。二、实验设备 PC 机一台，TD-ACC+(或 TD-ACS)教学实验系统一套。三、实验容1.典型的二阶

8、系统稳定性分析(1)构造框图(2)对应的模拟电路图(3)理论分析系统开环传递函数为：；开环增益。(4)实验容先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值，再将理论值应用于模拟电路中，观察二阶系统的动态性能及稳定性，应与理论分析根本吻合。，系统闭环传递函数为：其中自然振荡角频率：；阻尼比：。2.典型的三阶系统稳定性分析(1)构造框图(2)模拟电路图(3)理论分析系统的开环传函为:(其中)，系统的特征方程为:。(4)实验容实验前由 Routh 判断得 Routh 行列式为：为了保证系统稳定，第一列各值应为正数，所以有得： 0 < K < 12 Þ R > 41.7K系

9、统稳定K = 12Þ R = 41.7K系统临界稳定K > 12Þ R < 41.7K系统不稳定四、实验步骤及波形 1.将信号源单元的“ST端插针与“S端插针用“短路块短接。由于每个运放单元均设臵了锁零场效应管，所以运放具有锁零功能。将开关设在“方波档，分别调节调幅和调频电位器，使得“OUT端输出的方波幅值为 1V，周期为 10s 左右。 2.典型二阶系统瞬态性能指标的测试 (1)按模拟电路图 1.2-2 接线，将 1 中的方波信号接至输入端，取 R = 10K。 (2)用示波器观察系统响应曲线 C(t)，测量并记录超调 MP、峰值时间 tp 和调节时间 tS。

10、 (3)分别按 R = 50K；160K；200K；改变系统开环增益，观察响应曲线 C(t)，测量并记录性能指标 MP、tp 和 tS，及系统的稳定性。并将测量值和计算值进展比较 (实验前必须按公式计算出)。将实验结果填入表 1.2-1 中。参数工程R (K)KnC(tp)C()Mp (%)tp(s)ts(s)响应 情 况理 论 值 测量 值理 论 值测 量 值理 论 值测量值0<<1欠阻尼10 20 10 1/4 1.41 4438.82 0.32 0.2961.6 1.344 衰 减 振 荡504 4.47 0.56 1.1 1 11 7.76 0.85 0.7661.6 1.

11、0471 临界 阻尼 160 1.252.51 无1无无 1.9 3.672 单 调 指 数> 1过阻尼2001 2.24 1.12无 1无无 2.9 4.844 单 调 指 数系统响应曲线如下： 欠阻尼 R=10K 欠阻尼R=50 K临界阻尼R=160 K 过阻尼R=200 K3.典型三阶系统的性能(1)按图 1.2-4 接线，将 1 中的方波信号接至输入端，取 R = 30K。(2)观察系统的响应曲线，并记录波形。(3)减小开环增益 (R = 41.7K；100K)，观察响应曲线，并将实验结果填入表 1.2-3 中。R(K)开环增益 K稳定性30167不稳定发散41 .712临界稳定

12、等幅振荡1005稳定衰减收敛不同开环增益下的的响应曲线： K=16.7R=30 K K=12R=41.7 K K=5R=100 K实验报告课程名称：自动控制原理实验工程：控制系统的稳定性和稳态误差实验地点：自动控制实验室指导教师：乔学工实验三控制系统的稳定性和稳态误差一、实验目的1学会利用MATLAB对控制系统的稳定性进展分析；2学会利用MATLAB计算系统的稳态误差。二、实验设备安装Windows系统和MATLAB软件的计算机一台。三、实验容1.利用MATLAB描述系统数学模型如果系统的的数学模型可用如下的传递函数表示则在MATLAB下，传递函数可以方便的由其分子和分母多项式系数所构成的两个

13、向量惟一确定出来。即num=b0,b1 , bm; den=1,a1,a2 ,an例2-1假设系统的传递函数为试利用MATLAB表示。解对于以上系统的传递函数，可以将其用以下MATLAB命令表示>>num=4;den=1,3,2,5;printsys(num,den)结果显示：num/den = 4 - s3 + 3 s2 + 2 s+5当传递函数的分子或分母由假设干个多项式乘积表示时，它可由MATLAB 提供的多项式乘法运算函数conv( )来处理，以获得分子和分母多项式向量，此函数的调用格式为 p=conv(p1,p2)其中，p1和p2分别为由两个多项式系数构成的向量，而p为p

14、1和p2多项式的乘积多项式系数向量。conv( )函数的调用是允许多级嵌套的。例2-2假设系统的传递函数为试利用MATLAB求出其用分子和分母多项式表示的传递函数。解：对于以上系统的传递函数，可以将其用以下MATLAB命令表示>>num=4*1,6,6;den=conv(1,0,conv(1 1,1,3,2,5);printsys(num,den)结果显示：num/den = 4 s2 + 24 s + 24 - s5 + 4 s4 + 5 s3 + 7 s2 + 5 s2利用MATLAB分析系统的稳定性在分析控制系统时，首先遇到的问题就是系统的稳定性。判断一个线性系统稳定性的一种

15、最有效的方法是直接求出系统所有的极点，然后根据极点的分布情况来确定系统的稳定性。对线性系统来说，如果一个连续系统的所有极点都位于左半s平面，则该系统是稳定的。MATLAB中根据特征多项式求特征根的函数为roots( )，其调用格式为r=roots(p)其中，p为特征多项式的系数向量；r为特征多项式的根。另外，MATLAB中的pzmap( )函数可绘制系统的零极点图，其调用格式为p,z=pzmap(num,den)其中，num和den分别为系统传递函数的分子和分母多项式的系数按降幂排列构成的系数行向量。当pzmap( )函数不带输出变量时，可在当前图形窗口中绘制出系统的零极点图；当带有输出变量时

16、，也可得到零极点位置，如需要可通过pzmap(p,z)绘制出零极点图，图中的极点用“×表示，零点用“o表示。例2-3系统的传递函数为给出系统的零极点图，并判定系统的稳定性。解利用以下MATLAB命令>>num=3 2 1 4 2;den=3 5 1 2 2 1;>>r=roots(den),pzmap(num,den)执行结果可得以下极点和如图2-1所示的零极点图。r = -1.6067 0.4103 + 0.6801i 0.4103 - 0.6801i -0.4403 + 0.3673i -0.4403 - 0.3673i由以上结果可知，系统在右半s平面有两

17、个极点，故系统不稳定。图2-1 零极点图3利用MATLAB计算系统的稳态误差对于图2-2所示的反响控制系统，根据误差的输入端定义，利用拉氏变换终值定理可得稳态误差ess图2-2 反响控制系统在MATLAB中，利用函数dcgain( )可求取系统在给定输入下的稳态误差，其调用格式为ess=dcgain (nume,dene)其中，ess为系统的给定稳态误差；nume和dene分别为系统在给定输入下的稳态传递函数的分子和分母多项式的系数按降幂排列构成的系数行向量例2-4单位反响系统的开环传递函数为试求该系统在单位阶跃和单位速度信号作用下的稳态误差。解 (1) 系统在单位阶跃和单位速度信号作用下的稳

18、态传递函数分别为(2) MATLAB命令为>>nume1=1 2 1;dene1=1 2 2;ess1=dcgain (nume1,dene1)>>nume2=1 2 1;dene2=1 2 2 0;ess2=dcgain (nume2,dene2)执行后可得以下结果。ess1 = 0.5000ess2 = Inf四实验结果例2-1>> num=4;>> den=1,3,2,5;>> printsys(num,den);num/den = 4 - s3 + 3 s2 + 2 s + 5例2-2>> num=4*1,6,6;

19、>> den=conv(1,0,conv(1,1,1,3,2,5);>> printsys(num,den);num/den = 4 s2 + 24 s + 24 - s5 + 4 s4 + 5 s3 + 7 s2 + 5 s例2-3>> num=3,2,1,4,2;den=3,5,1,2,2,1;>> r=roots(den),pzmap(num,den)r = -1.6067 + 0.0000i 0.4103 + 0.6801i 0.4103 - 0.6801i -0.4403 + 0.3673i -0.4403 - 0.3673i例2-4&

20、gt;> nume1=1 2 1;dene1=1 2 2;ess1=dcgain(nume1,dene1)ess1 = 0.5000>> nume2=1 2 1;dene2=1 2 2 0;ess2=dcgain(nume2,dene2)ess2 = Inf五实验心得实验报告课程名称：自动控制原理实验工程：控制系统的根轨迹和频域特性分析实验地点：自动控制实验室实验日期： 2021 年 3 月 22 日实验四控制系统的根轨迹和频域特性分析一、实验目的1学会利用MATLAB绘制系统的根轨迹，并对系统进展分析；2学会利用MATLAB对系统进展频域特性分析。二、实验设备安装Windo

21、ws系统和MATLAB软件的计算机一台。三、实验容1基于MATLAB的控制系统根轨迹分析1利用MATLAB绘制系统的根轨迹利用rlocus( )函数可绘制出当根轨迹增益k由0至+变化时，闭环系统的特征根在s平面变化的轨迹，该函数的调用格式为r,k=rlocus(num,den) 或 r,k=rlocus(num,den,k)其中，返回值r为系统的闭环极点，k为相应的增益。rlocus( )函数既适用于连续系统，也适用于离散系统。rlocus(num,den)绘制系统根轨迹时，增益k是自动选取的，rlocus(num,den, k)可利用指定的增益k来绘制系统的根轨迹。在不带输出变量引用函数时，

22、rolcus( )可在当前图形窗口中绘制出系统的根轨迹图。当带有输出变量引用函数时，可得到根轨迹的位置列向量r及相应的增益k列向量，再利用plot(r,*)可绘制出根轨迹。2利用MATLAB获得系统的根轨迹增益在系统分析中，常常希望确定根轨迹上*一点处的增益值k，这时可利用MATLAB中的rlocfind( )函数，在使用此函数前要首先得到系统的根轨迹，然后再执行如下命令k,poles=rlocfind(num,den) 或 k,poles=rlocfind(num,den,p)其中，num和den分别为系统开环传递函数的分子和分母多项式的系数按降幂排列构成的系数向量；poles为所求系统的闭

23、环极点；k为相应的根轨迹增益；p为系统给定的闭环极点。3实验上机结果： 1. *反响系统的开环传递函数为试绘制该系统根轨迹，并利用根轨迹分析系统稳定的k值围。程序：>> num=1;den=conv(1,0,conv(1,1,1,2);>> rlocus(num,den);k,poles=rlocfind(num,den)执行以上命令，并移动鼠标到根轨迹与虚轴的交点处单击鼠标左键后可得根轨迹和如下结果：Select a point in the graphics windowselected_point = 0.0024 + 1.3975ik = 5.8689poles

24、 = -2.9880 + 0.0000i -0.0060 + 1.4015i -0.0060 - 1.4015i分析：由此可见根轨迹与虚轴交点处的增益k=6，这说明当k<6时系统稳定，当k>6时，系统不稳定；利用rlocfind( )函数也可找出根轨迹从实轴上的别离点处的增益k =0.38, 这说明当0<k<0.38时，系统为单调衰减稳定，当0.38<k<6时系统为振荡衰减稳定的。2. *正反响系统的开环传递函数如1所示。试绘制系统根轨迹，并计算根轨迹上点-2.3±j2.02处的根轨迹增益和此时系统的稳定性。程序如下:>>num=1;den=conv(1,0,conv(1,1,1,2);>>rlocus(-num,den);k,