chapter矩阵与行列式小结

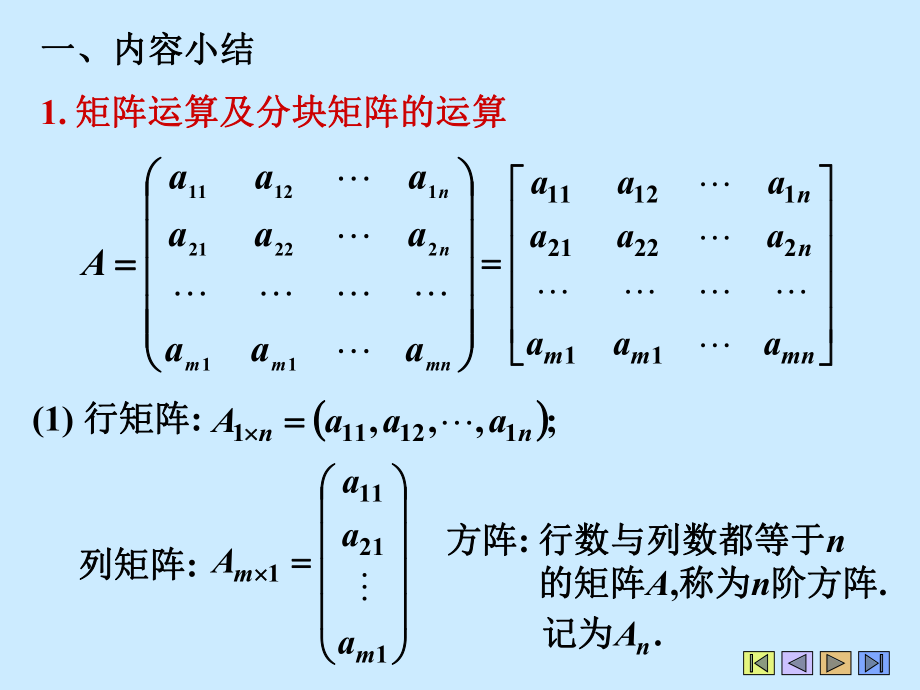
1、一、内容小结一、内容小结2. 行列式定义和性质行列式定义和性质3. 关于行列式的一些重要公式关于行列式的一些重要公式1. 矩阵运算及分块矩阵的运算矩阵运算及分块矩阵的运算4. 关于逆矩阵的一些重要结论关于逆矩阵的一些重要结论5. 初等变换与初等矩阵初等变换与初等矩阵6. 克莱姆法则克莱姆法则7. 注意比较注意比较二、题型及方法二、题型及方法1. 行列式的计算行列式的计算2. 逆矩阵的求法逆矩阵的求法3. 矩阵的秩的求法矩阵的秩的求法4. 矩阵方程的解法矩阵方程的解法5. Gramer法则的应用法则的应用一、内容小结一、内容小结1. 矩阵运算及分块矩阵的运算矩阵运算及分块矩阵的运算 mnmmnn

2、aaaaaaaaaA112222111211 mnmmnnaaaaaaaaa112222111211(1) 行矩阵行矩阵: ;,112111nnaaaA 列矩阵列矩阵: 121111mmaaaA方阵方阵: 行数与列数都等于行数与列数都等于n的矩阵的矩阵A,称为称为n阶方阵阶方阵.nA记记为为(2) 零矩阵零矩阵(3) 上上(下下)三角方阵三角方阵 mnnnaaaaaa00022211211(4) 对角方阵对角方阵(5) 单位矩阵单位矩阵(方阵方阵)(6) 矩阵矩阵A,B同型同型(7) 相等矩阵相等矩阵(8) 阶梯形矩阵阶梯形矩阵(9) 对称矩阵对称矩阵 nnnnnnaaaaaaaaa21222

3、1211211(10) 反对称矩阵反对称矩阵 00021212112nnnnaaaaaa(11) 伴随矩阵伴随矩阵 mnmnmmmmnnnnbababababababababaBA221122222221211112121111 112222111211 mnmmnnkakakakakakakakakakA加法：加法：数乘：数乘： skkjiksjisjijiijbabababac12211 , 2 , 1;, 2 , 1njmi 并把此乘积记作并把此乘积记作.ABC 设设 是一个是一个 矩阵，矩阵， 是一个是一个 矩阵，那末规定矩阵矩阵，那末规定矩阵 与矩阵与矩阵 的乘积的乘积是一个是一个

4、矩阵矩阵 ，其中，其中 ijaA sm ijbB ns nm ijcC AB乘法：乘法：乘方，转置，共轭乘方，转置，共轭分块矩阵也有这些运算分块矩阵也有这些运算. rrBOBOBAOAOAAB2121.2211 rrBAOBAOBA,11 srAAA设设rA11sA.11TTsrTTAAA 则则TsA1TrA1TsA1TrA1.11 TsrTTAAA则则注意要转置两次注意要转置两次.2. 行列式的定义和性质行列式的定义和性质定义定义 2122221112112nnnnnnaaaaaaaaaDnn 阶阶行行列列式式个个数数组组成成的的由由是一个算式，且是一个算式，且,1 ,1 ,11121211

5、1111111 nAaAaAaAanaDnnnjjj.), 2 , 1(11的代数余子式的代数余子式是是其中其中njaAjj 定义定义. 代数余子式代数余子式 ,212222111211列列行行与与第第所所在在的的第第中中划划去去元元素素在在jiaaaaaaaaaaijnnnnnn剩下的元素按原来的排法构成一个新的行列式剩下的元素按原来的排法构成一个新的行列式,111111111111111111111111ijnnnjnjnnijijiinijijiinjjMaaaaaaaaaaaaaaaa记为记为 .)1( ;,的代数余子式的代数余子式称为称为而而记为记为的余子式的余子式称为元素称为元素i

6、jijjiijijijaMAMa 行列式与它的转置行列式相等行列式与它的转置行列式相等. . 互换行列式的两行（列）互换行列式的两行（列）, ,行列式变号行列式变号. .推论推论 如果行列式有两行如果行列式有两行( (列列) )完全相同完全相同, ,则行列式为零则行列式为零. . 行列式的某一行（列）中所有的元素都行列式的某一行（列）中所有的元素都乘以同一数乘以同一数 ，等于用数，等于用数 乘此行列式乘此行列式. .kk行列式的某一行（列）中所有元素的公因行列式的某一行（列）中所有元素的公因子可以提到行列式符号的外面子可以提到行列式符号的外面性质性质行列式中如果有两行（列）元素成比行列式中如果

7、有两行（列）元素成比例，则此行列式为零例，则此行列式为零性质性质5 5若行列式若行列式D的某一列（行）的元素都是的某一列（行）的元素都是两数之和，两数之和，则则D等于下列两个行列式之和等于下列两个行列式之和.nnnininnniiniiaaaaaaaaaaaaaaaD)()()(2122222211111211 nnninnininnninniniaaaaaaaaaaaaaaaaaaD 122211111122211111性质性质把行列式的某一列（行）的各元素乘以把行列式的某一列（行）的各元素乘以同一数然后加到另一列同一数然后加到另一列(行行)对应的元素上去，行对应的元素上去，行列式不变列式不

8、变性质性质7. 行列式按行（列）展开法则行列式按行（列）展开法则 ;,0,1jijiAAAaijnkkjki当当当当 ;,0,1jijiAAAaijnkjkik当当当当 .,0,1jijiij当当，当当其其中中性质性质8. Laplace定理定理3. 关于行列式的一些重要公式关于行列式的一些重要公式AA )1(11)2( AA1*)3( nAAAkkAn )4(BAAB )5(BAkkABn )6( jijiAAajijiAAankkjkinkjkik 0 , 0 )7(11BAOBAOBABCOABABOCAmn)1( , ,)8( kkAAAAOAOAA2121)9( . )10(主对角线

9、上元素的乘积主对角线上元素的乘积式的值为式的值为三角行列式与对角行列三角行列式与对角行列nnnnOO 212)1(21)1()11( 行行列列式式eVandermond)12(112112222121111 nnnnnnnxxxxxxxxxD)( )()()(122311312 nnnnxxxxxxxxxxxx njiijxx1)(4. 关于逆矩阵的一些重要结论关于逆矩阵的一些重要结论ABBAEBAAB 11,)1(则则若若EAAAAA *)2(*11, 0)3(AAAAA 且且可可逆逆1111111)( ,1)( ,)(4( ABABAAAA )()()( ,)()(11111 BAABAA

10、*1*11*)( ,1)()(5(AkkAAAAAn AAAAAnn2*1*)( ,)1()( acbddcba*:注注 11111. 6kkAOOAAOOA OAAOOAAOkk11111 11111. 7BOCBAABOCA 11111BCABOABCOA5. 初等变换与初等矩阵初等变换与初等矩阵定义定义.下面三种变换称为矩阵的初等行变换下面三种变换称为矩阵的初等行变换: ）；记记作作两两行行对对调调两两行行（对对调调jirrji,1 ;02乘乘以以某某一一行行的的所所有有元元素素以以数数 k）记记作作行行乘乘（第第krkii , .3 ）记记作作行行上上倍倍加加到到第第行行的的对对应应的

11、的元元素素上上去去（第第倍倍加加到到另另一一行行把把某某一一行行所所有有元元素素的的jikrrikjk 定义定义. . 由单位矩阵由单位矩阵E 经过一次初等变换得到的方经过一次初等变换得到的方 阵称为初等矩阵阵称为初等矩阵. .定理定理1. 任何矩阵任何矩阵A可以只用初等行变换化成阶梯形矩阵可以只用初等行变换化成阶梯形矩阵.定理定理2. 任何矩阵任何矩阵A可以用初等变换化成标准形矩阵可以用初等变换化成标准形矩阵.定理定理3. 初等变换不改变方阵的可逆性与不可逆性初等变换不改变方阵的可逆性与不可逆性.定理定理4. .EAAn 可可逆逆阶阶方方阵阵 定理定理5 5 设设 是一个是一个 矩阵，对矩阵

12、，对 施行一施行一次初等行变换，相当于在次初等行变换，相当于在 的左边乘以相应的的左边乘以相应的 阶初等矩阵；对阶初等矩阵；对 施行一次初等列变换，相当于施行一次初等列变换，相当于在在 的右边乘以相应的的右边乘以相应的 阶初等矩阵阶初等矩阵. .nm mnAAAAA可可逆逆A)1(0 AEA 的的乘乘积积可可表表成成有有限限个个初初等等矩矩阵阵A化化成成单单位位矩矩阵阵可可经经有有限限次次初初等等行行变变换换A等等价价与与BA)2(BPAQQP 使得使得存在可逆矩阵存在可逆矩阵,经初等变换得到经初等变换得到可由可由AB)()(BrankArank 6. 克莱姆法则克莱姆法则定理定理1. 如果线

13、性方程组的系数行列式不等于如果线性方程组的系数行列式不等于0，则方，则方 程组一定有解，且解是唯一的程组一定有解，且解是唯一的.定理定理2. 如果线性方程组无解或有两个不同的解，则如果线性方程组无解或有两个不同的解，则 它的系数行列式必为它的系数行列式必为0.推论推论1. 如果齐次线性方程组的系数行列式如果齐次线性方程组的系数行列式 则齐次线性方程组只有唯一零解则齐次线性方程组只有唯一零解., 0 A推论推论2. 如果齐次线性方程组有非零解，则它的如果齐次线性方程组有非零解，则它的 系数行列式系数行列式. 0 A7. 注意比较注意比较BAABABABABAB ,)( ,)(1(111BABAB

14、ABABABA ,)( ,)(2(111 )3(以下为错误的表达式以下为错误的表达式2222)(BABABA 22)(BABABA CBOAACAB 则则且且若若,EAEAEA 或或则则若若,20, AOA则则若若AA BABA 二、题型及方法二、题型及方法1. 行列式的计算行列式的计算方法一、方法一、利用行列式的性质，或通过将行列式化为利用行列式的性质，或通过将行列式化为三角行列式来计算行列式的值三角行列式来计算行列式的值. .方法二、方法二、当行列式各行当行列式各行( (列列) )元素之和相同时，应先元素之和相同时，应先把各列把各列( (行行) )加到第加到第1 1列列( (行行) )，提

15、取公因式后再考虑，提取公因式后再考虑. .方法三、方法三、根据行列式的特点，利用行列式的性质，根据行列式的特点，利用行列式的性质，将行列式的某一行将行列式的某一行( (列列) )化出尽量多的化出尽量多的0 0元素，然后元素，然后由定义按该行由定义按该行( (列列) )展开展开. .方法四、方法四、当各阶行列式具有同一结构形式时，可利当各阶行列式具有同一结构形式时，可利用数学归纳法计算或证明行列式的值用数学归纳法计算或证明行列式的值. .方法五、方法五、先用展开或拆项等方法，将原行列式表成先用展开或拆项等方法，将原行列式表成低阶同型行列式的线性关系，再由递推法得出结果低阶同型行列式的线性关系，再

16、由递推法得出结果. .方法六、方法六、当行列式为三线非当行列式为三线非0 0行列式时，将其转化为行列式时，将其转化为三角行列式来计算三角行列式来计算. . 方法七、方法七、加边法，即在行列式值不变的情况下，加加边法，即在行列式值不变的情况下，加上一行一列上一行一列. . 用于主对角线上元素不同，其余元素用于主对角线上元素不同，其余元素相同相同( (或各行其余元素成比例或各行其余元素成比例) )的行列式的行列式. .2. 逆矩阵的求法逆矩阵的求法(1)利用定义及恒等变形得到利用定义及恒等变形得到 (用于证明题或不知道用于证明题或不知道A的具体内容的具体内容)*11)2(AAA 利用公式利用公式(

17、3)利用初等行变换利用初等行变换 1 AEEA行行(4)利用分块矩阵来求逆矩阵利用分块矩阵来求逆矩阵3. 矩阵的秩的求法矩阵的秩的求法)(0(ArankA行的个数即行的个数即非非阶梯形矩阵阶梯形矩阵行行4. 矩阵方程的解法矩阵方程的解法BAXBAX1)1( XEBAEBA 1行行即即1)2( BAXBXA XEBAEBA1列列即即5. Gramer法则的应用法则的应用199421022130113. 1 计算计算exSolution.120042210021130013199421022130113 142221113200421002130013 1422211130 252414446 0

18、)3()2()1()3()2()1()3()2()1()3()2()1(. 22222222222222222 ddddccccbbbbaaaaDex 证证明明Solution.5232125232125232125232122222 ddddccccbbbbaaaaD42124212421242122222 ddccbbaa0 3111131111311113. 3 Dex 计算计算Solution.4321rrrrD 311113111131666631111311113111116 141312rrrrrr 2000020000201111648 bacccbacbbaacbaex 22

19、2222. 4 计计算算Solution.bacccbacbbcbacbacba 2222原原式式bacccbacbbcba 2222111)(baccacbbcba 0202001)(.)(3cba 110000030000220000111321. 5 nnnnex计计算算Solution.110000030000220000101322)1( nnnnnn原式原式11000000002200012)1( nnnn)1()2)(1(2)1( nnn)!1()1(2)1(1 nnnn)!.1()1(211 nnnex2222223222222222221. 6计计算算Solution.200

20、00001002222200001 n原式原式200000102222)1( n)!.2(2)1( n., 0 ,. 7BABAEBBBBEAAAAnBAex 求求及及满满足足阶阶方方阵阵为为设设Solution.ABBA , 0EBAEBA 而而BAABBA BABA)( BBAA)( BBAA)( BBAA)( BBAA BAA 20)1(2 BAA故故0 BA,3. 8333222111333222111 dcbdcbdcbBdcadcadcaAex阶阶方方阵阵设设有有. |,21| , 2|BABA 求求且且已已知知Solution.333322221111222222|dcbadcb

21、adcbaBA 333222111333222111222222222222dcbdcbdcbdcadcadca .10|4|4 BAex9. |)( | |,2|, 5| , 3|,100,1 ABABBABA求求且且阶阶方方阵阵为为设设Solution.;215|2|2|100100 BAAB.15115|)|(|)( |1111 BAABAB,22OEAA 由由 EEAA2 得得, 0 AEEAA 212 EAA.,2,:,22并并求求它它们们的的逆逆矩矩阵阵都都可可逆逆证证明明满满足足方方程程设设方方阵阵EAAOEAAA ex10.可可逆逆故故A1 A .211EAA Solution

22、.OEAA 22又又由由 OEEAEA 432 EEAEA 3412.EA可逆可逆故故2 EAEA34121 且且.43AE 12 EA , 13412 EAEAex11 求方阵求方阵 的逆矩阵的逆矩阵. . 343122321ASolution.343122321 A, 02 .1存在存在 A, 2341211 A, 3331212 A同理可得同理可得, 2, 6, 6, 223222113 AAAA, 2, 5, 4333231 AAA,222563462 A得得故故 AAA11 22256346221.11125323231 .,0000000000000000.121121 Aaaaa

23、Aexnn求求设设Solution. OaAOAnn 1记记 OAaOAnn1111则则 00000000000000001112111nnaaaa.,3800026000002000001200011.131 AAex求求设设Solution.,321 AOAOAA,3826),2(,1211321 AAA,12111211111 A),21(12 A,6823213826113 A 1312111AOAOAA.340001230000021000001200011 .234311111012110:.14OXex 解解矩矩阵阵方方程程Solution.,BXA 100010001 1110

24、12110 001010100 110012111 001213100 110100111 213001100 100110111 213212113 100010011 213212305 100010001,2132123051 A1 BAX 234311 213212305.658326 ex15. 用初等变换法求解下列矩阵方程用初等变换法求解下列矩阵方程:.1000210012103211000110011101111 nnnXSolution. 1000100021001100121011103211111nnn 10001000110001001110001011110001.10

25、00110011101111 X.,2001,2111,.16101ADPDAPPex求求其其中中设设 Solution.,1 PDPA,1112211111 P11010 PPDA1020012111 1112 1020012111 1112 11102121 1112.1222122211111010 .,101020101 ,3.172BABAEABBAex求求且且满满足足阶阶方方阵阵设设 Solution.,2EABAB ),)()(EAEABEA 001010100| EA, 01 .可逆可逆EA )(EAB .201030102 .,161117231461203211.18的秩的秩求求设设AbaAex Solution. babaA4420126101221003211161117231461203211 020000008001221003211ba; 2)(,2, 8 Arba时时且且当当; 3)(,2, 8 Arba时时且且当当; 3)(,2, 8 Arba时时且且当当. 4)(,2, 8 Arba时时且且当当. 3)(, 2)(, ,2111212112.192 ArAraaaAex使使的值的值确定确定设设Solution. 2112121211211121211222aaaaA 22330330211222aaaa 2000330211222a