路基过渡段动力仿真分析

1、路基过渡段动力仿真分析路基与横向结构物主要有路基与桥梁、路基与隧道、路基与涵洞以及路堤与路堑等，由于行车速度的提高，在上述两两之间设置过渡段，以确保列车运行平稳过渡。在上述过渡段中，以路基与桥梁最为重要，路基与隧道的过渡特点与路基与桥梁类似。以下只针对路基与桥梁和路基与涵洞动力仿真分析。1 路基与桥梁过渡段动力仿真分析1.1 路基与桥梁过渡段动力特性的评价指标与路桥过渡长度的确定方法蔡成标等针对轨道过渡段中具有普遍性和典型性的路桥过渡段建立了动力学分析模型，提出了一套列车 -轨道过渡段动力特性的评价指标，并进行了大量的计算分析，提出了合理确定路桥过渡长度的方法。对于路桥过渡段而言，以桥上铺设长

2、轨枕埋入式无碴轨道时与路基上有碴轨道连接最为典型，其过渡段模型如 图 1 所示。图 1 路桥过渡段动力分析模型在列车 -路桥过渡段动力学分析模型中， 将机车车辆模拟成一个以速度V 运行于线路上的多刚体系统，模型反映了车体质量和点头惯量、前后转向架构架质量和惯量、轮对质量，以及一、二系悬挂特性；考虑了车体及前、后转向架的沉浮和点头运动，以及轮对的垂向振动。钢轨为连续弹性点支承基础上的无限长Euler 梁，各支承点以轨枕间距隔开；分别考虑轨下胶垫、道床和路基的刚度与阻尼的作用；道1床离散模型采用锥体分布假设，并考虑了其剪切作用。轮轨相互作用力由Hertz 非线性弹性接触理论确定。另外，假定轨道沉降

3、和刚度在过渡段均匀变化。轨道几何不平顺包括随机不平顺和由沉降差引起的轨面高度变化。车辆系统的动力学方程由D Alembert 原理获得，轨道系统的动力学方程中需要将钢轨四阶偏微分方程转化成普通二阶常微分方程组。最后，可将列车一轨道系统的动力学方程写成如下标准形式MX ¨ + CX·+ KX = F为了高效快速求解这一大型振动系统响应，这里采用的快速数值积分方法，从而在普通微机上实现了列车-路桥过渡段系统的动力学仿真分析。在分析列车与路桥过渡段的动力特性时，选用SS8 机车牵引准高速双层客车(一动三拖为例 )以及中国干线轨道的基本参数。在实际线路中，轨道不平顺是客观存在的，而

4、且是随机的。作者采用了目前应用较广泛的美国六级谱。图 2 为 150 m 范围内，轨道随机不平顺的数值模拟结果。图 2 轨道随机不平顺数值模拟样本在轨道过渡段中，除了随机不平顺外还存在由于地基(或填土 )沉降差引起的轨面高度变化。为了完整分析和评价列车通过轨道过渡段时系统的动力学性能，作者特选取下列评价指标： (a)轮轨力 Fwr ；(b)钢轨支点压力 Fr；(c)路基基床表面应力 f；(d)钢轨加速度 ar； (e)轨枕加速度 as；(f) 道床加速度 ab； (g)车体加速度 av；(h) 车轮悬浮量yw。路桥过渡段动力仿真分析主要成果与结论如下。2A 钢轨初始变形曲线分析。由于路、桥是二

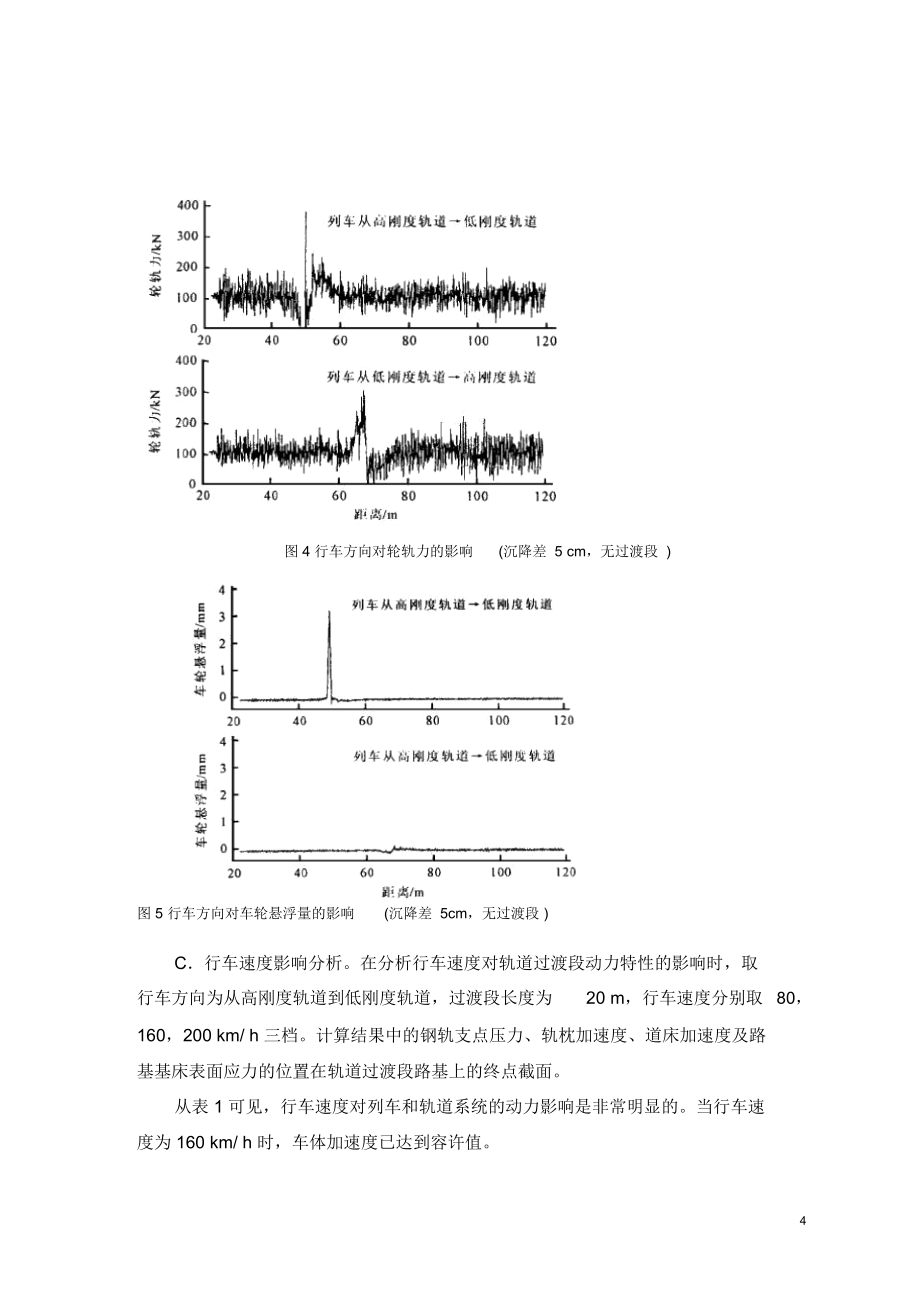
5、种性质差异巨大的工程结构物，必然产生工后沉降差。因此，钢轨就存在较大的且确定的初始变形，它只与沉降差有关。在以往的轨道过渡段动力学分析模型中， 假设轨道折角的做法是偏于保守的，作者提出的模型则更加符合实际。图 3 为沉降差 5 cm 时不设置过渡段及设置 20m 长的过渡段情况下，钢轨的初始变形曲线。图中两虚线间的距离在为不设置过渡段情况下，地基沉降差在低刚度轨道上影响轨面高度变化的范围。因此，过渡段的长度必须大于这一范围才能减缓轨面高度变化的速率。B行车方向影响分析。在不设置过渡段的情况下，列车出桥要比进桥危害更大。若设置过渡段则两者的动力作用差别不大。行车速度对列车与路桥过渡段的动力作用影

6、响很大。速度越高，动力作用越大。当沉降差为5 cm 时，对于 SS8牵引的准高速列车，速度160 km/h 时，车体加速度已达限值。在分析行车方向对动力作用的影响时，取沉降差为5cm，且分设置过渡段和不设置过渡段 2 种工况。在轨道有沉降差但不设置过渡段的情况下，从轮轨力(图 4)及车轮悬浮量 (图 5)来看，列车从高刚度轨道到低刚度轨道要比列车从低刚度轨道到高刚度道更为不利，特别是很大的车轮悬浮量将对行车安全造成很大的威胁。地基沉降差对列车与路桥过渡段的动力作用影响显著。随着沉降差的增大，动力作用急剧增大。因此，应采取一切可能措施降低桥台前土路基轨道的沉降。图 3 沉降差引起的钢轨变形曲线(

7、沉降差 5 cm)3图 4 行车方向对轮轨力的影响(沉降差 5 cm，无过渡段 )图 5 行车方向对车轮悬浮量的影响(沉降差 5cm，无过渡段 )C行车速度影响分析。在分析行车速度对轨道过渡段动力特性的影响时，取行车方向为从高刚度轨道到低刚度轨道，过渡段长度为20 m，行车速度分别取80，160，200 km/ h 三档。计算结果中的钢轨支点压力、轨枕加速度、道床加速度及路基基床表面应力的位置在轨道过渡段路基上的终点截面。从表 1 可见，行车速度对列车和轨道系统的动力影响是非常明显的。当行车速度为 160 km/ h 时，车体加速度已达到容许值。4表 1 行车速度对轮轨系统动力性能的影响-1F

8、wr /kNFr/kN-2-2-2ab/m ·s-2 f/MPaV/km ·hav/m·sar/m·sas/m·s80156.28037.0310.504231.5432.0466.6440.064160200.42044.8921.601459.70064.73514.8920.078200226.21050.3872.112602.25081.95518.9640.087D过渡段长度的确定在确定轨道过渡段长度时，针对相同的沉降差5、二，分别计算不同的轨道过渡段长度 ( 10 m ， 20m ， 30 m)时的动力响应，其中轮轨力及车体加速度

9、响应如图 6，图 7 所示。图 6 和图 7 中，两虚线问的距离为轨道过渡段的长度。可见，当轨道沉降差为5 cm 时，若过渡段的长度取10 m，则轮轨力及车体加速度均有较大的波动，而过渡段长度为 20 m 及 30 m 时，两种工况的动力响应已无明显差别，因此过渡段长度可取 2025 m。路桥过渡段的长度应根据最高行车速度、基础沉降差，由动力学评判指标来确定，其中车体加速度和路基基床表面应力起控制作用。 经计算分析，当沉降差为 5 cm 时，过渡段长度为 20 m25 m；当沉降差为 10 cm 时，过渡段长度为 25 m30 m；当沉降差为 15 cm 时，过渡段长度为 30 m35 m。图

10、 6 过渡段长度对轮轨力的影响(沉降差 5)5图 7 过渡段长度对车体心盘处加速度的影响(沉降差 5 cm)1.2 路桥结构的不均匀沉降引起的轨面弯折变形对行车的影响罗强等研究了路桥结构的不均匀沉降引起的轨面弯折变形对行车的影响。作者以车辆、线路系统力学为基础，进行高速铁路路桥过渡段轨道动力学性能的理论分析，研究各种不平顺因素对列车运行的影响规律，建立高速列车与路桥过渡段相互作用力学分析模型，开发数值仿真软件，对不同轨下基础轨道连接中具有典型意义的路桥过渡段的动力学性能， 就各种不同工况条件， 进行了大量的计算机仿真计算、综合分析和性能评价。为了全面分析高速列车通过路桥过渡段时车辆与线路相互作

11、用的特性，寻求合理的过渡段设计参数，罗强，蔡英运用车辆 -轨道 -路基大系统的动力学理论，建立了如图 8 所示的线路、车辆竖向耦合振动分析模型。车体被简化为一个刚体，有点头和沉浮两个自由度。每个转向架也被简化为刚体，也有点头和沉浮两个自由度。轮对和簧下质量简化成质量块，各部件之间由弹簧和阻尼器连接。线路为钢轨、轨枕、道床和路基组成的 3 层点支承梁模型。钢轨为连续支承欧拉梁，轨枕被简化为刚体，道床被离散化为集中质量块。6图 8 车辆轨道路基竖向振动分析模型模型中高速铁路线路、车辆的基本计算参数主要参考了有关文献的数据和国家“八五”科技攻关项目中有关高速铁路的研究成果。图 9 过渡段轨道基础刚度

12、变化示意图图 10 过渡段轨面弯折变形示意图过渡段的不平顺主要考虑了2 种类型共 3 种工况： (a)轨面平顺，路桥间轨道基础的刚度变化如 图 9 所示； (b)轨面产生如 图 10 所示的弯折变形，轨道基础的刚度差为零； (c)轨面产生如 图 10 所示变形的同时，轨道基础的刚度变化如图2 所示。工况 (a)主要模拟过渡段线路的轨面经起拨道调整后，仅由路桥间轨道基础的刚度差引起轨道刚度的变化对高速行车的影响；工况 (b)主要模拟轨道的刚度均匀(即路7桥间的刚度差为零 )时，仅由路桥间的沉降差引起线路轨面的弯折变形对高速行车的影响；工况 (c)是路桥过渡段不平顺的实际工况，主要模拟线路轨面的弯

13、折变形与轨道基础刚度的变化对高速行车的综合影响。在行车速度 V= 350 km/h、过渡段长度 L= 20 m 条件下，轨面的弯折角 ()和路桥间轨道基础刚度差 (桥台刚度 /路基刚度 =1×10m 的变化对轮轨垂向力 (p)和车体垂向加速度 (av)等指标的影响如表2 所示。桥面为有砟轨道结构，列车由路基向桥台方向行驶。表 2动力学计算数据表 / P/kN-2av/(m ·s)m= 0m= 1m= 2m= 0m= 1m= 20960.0496960.030.040.042.51811862041.491.491.495.02592723253.203.213.217.53

14、393794534.784.784.7810.04384935926.106.106.1112.55306127289.209.229.22（a）工况 1过渡段轨道基础刚度变化的影响在= 0 条件下， m 的变化对 p 基本无影响，对av 的影响也甚微，距有关舒适安全控制标准 (av0.13g，p1.8p0， p0静轮载 )还有相当大的距离，不成为设计控制条件。（b）工况 2过渡段轨面弯折变形的影响在 m=0 条件下， 的变化对 p 和 av 的影响十分剧烈，当 2.1 2.26时，就可能对乘座的舒适性和行车的安全性产生影响。（c）工况 3过渡段轨道基础刚度变化和轨面弯折变形的综合影响m 和

15、的综合作用对 p 和 av 的影响稍大，对 的限制稍严，在m= 2 条件下， 1.78 2.1后就可能对乘座舒适性和行车安全性产生影响。2 路基与涵洞过渡段动力仿真分析中南大学等单位对武广客运专线DK1252+679DK1252+731 高密集涵过渡段8路涵过渡段进行了仿真分析。基于有限元理论建立无砟轨道-路基 -地基计算模型，在复杂的约束和加载条件下，求解无砟轨道过渡段路基的动态响应。假定轨下基础各结构层都由均质、各向同性的弹性或弹塑性材料组成。地基层无限深度处及水平无限远处应力和应变均假设为零，各结构层之间位移通过不同约束方程连为一体。该段地基采用 CFG 桩加固，桩径 0.5m，按正三角

16、形布置，桩顶均铺设0.6m 厚的碎石垫层，内铺一层极限抗拉强度不小于80KN/m 的土工格栅。该工点为板式无砟轨道结构，实体的有限元模型见图11，仿真分析结果如下。图 11 涵 -涵过渡段有限元计算模型A.车速影响当只考虑车速的变化，车速取150km/h、 200km/h、 250km/h、 3000km/h 和350km/h 五挡。在浅层内（钢轨至混泥土承载层）动位移随车速的增加而减少，但过了某一深度以后（基床底层以下） ，随着深度的增加，动位移随车速的增加而增加。动速度、动加速度、动应力随车速的增加而增加。涵洞中心，对应的位移响应越小，而应力响应大。9B.填料影响为了研究路桥过渡段采用级配

17、碎石或级配碎石5%水泥填料填筑后， 动态响应是否发生影响，或者说有何影响，以下对其进行了仿真分析。车速取 350 km/h。设级配碎石 5%水泥为材料 1 即刚性大、弹性模量大的材料， 级配碎石为材料 2 即刚性小、弹性模量小的材料。仿真分析结果表明，过渡段填料的性质对其动态响应影响较大。刚性大、弹性模量大材料，其对应的位移、速度响应小，动应力响应大；而刚性小、弹性模量小材料对应的位移、速度响应大，动应力小。刚性越大，动力响应随深度的衰减越快；刚性越小，动力响应随深度的衰减越慢。C.过渡段长度的影响假定代表车辆为“ CRH2”火车，地基基础工后沉降为零，车速为350 km/h，过渡段长度分别取

18、11.4 m，12.6 m，14.4 m 和 15.6 m。仿真分析结果表明，过渡段长度对竖向动位移、动速度、动加速度影响不大。随着过渡段长度的增长，其对应的竖向动位移、动速度、动加速度呈减小的趋势，但并不是十分明显。随着过渡段长度的增加，对应的竖向动应力有所减小。总的来说过渡段长度的增加有利于减少路基面的动力响应，提高路基的长期稳定性。D.结构型式的影响涵涵过渡段路基采用正梯形或倒梯形结构型式，其动态响应有何变化，下面将对其进行对比仿真分析。车速取350 km/h。过渡段的结构型式无论是倒梯形还是正梯形，对其竖向动位移、动速度、动加速度影响不大，尤其在浅层深度内（1.0525877.5m）基

19、本上是重合的。而对于竖向动应力、动弹性应变，过渡段倒梯形结构型式的动力响应明显小于正梯形的（ 1.052587 7.5m），深度超过 7.5m 后，二者基本重合，无影响。这说明倒梯形比正梯形过渡段结构型式设计更为合理。E.折角的影响对于涵涵过渡段，铁路规范均设置了折角的限值。折角对过渡段结构的动态响应有何影响。下面将对其进行了研究。车速取350 km/h，过渡段长度 30m。过渡段10折角取 1：1.5，1：2.0，1：2.5 三种情况。折角 1： 1.5， 1： 2.0， 1： 2.5 过渡段折角对竖向动位移、动速度、动加速度影响并不大；但对基床表层动应力影响非常明显，随着深度的增加，折角动

20、应力的影响减弱。梁波等对京秦线提速要求，进行了提速路涵过渡段动力仿真动力仿真计算。计算分析了“神州号”内燃动车组 (2 动 3 拖)以 160 ，180 ，200 ， 220 和 250 km/ h 通过路涵过渡段加固前后的机车车辆运行安全舒适性指标、轨道及路基主要动力性能指标。并与随后的实车试验进行了对比。在此基础上对路涵过渡段加固方案提出评价意见与建议。仿真计算准确与否，涉及到计算模型准确性、参数取值影响计算条件变化影响等因素。作者在仿真计算中，同时考虑了轮轨作用力的随机因素、轨道随机不平顺性和路基刚度包括地基刚度的因素，能够反映路基参数变化和轨道主要工作特性对分析结果的影响。针对京秦既有

21、线路涵过渡段状态和试验加固段路涵过渡段的状态，分别计算不同提速速度下的路基动力响应以及机车车辆运行品质。具体计算的动力指标主要包括：路基表面压力 f、地基表面压力 s、基床表面加速度 as、道床顶面压力 b、轮轨作用力 P、轮重减载率 P/ P、乘坐舒适度指标或平稳性指标 -车体垂向振动加速度 ac 等。根据机车车辆运行安全性与舒适性评定标准以及路基和轨道动力性能指标限值对所分析的各种方案与工况提出有关评价意见或建议。作者计算了 160 ，180 ，200 ，220 ，250 km/ h 和普通路基段加固与未加固 2 种条件组合共计 10 个仿真计算工况，加固路基采用直径 0.3 m、间距 0

22、.6 m、桩长 1.0m 的混凝土挤密桩。11图 12车辆一路基竖向振动简化模型图 13 车辆计算简化模型动力分析模型和计算简化模型分别见图12 和图 13。模型中，车辆的车体和轮对均视为刚体；通过线路的列车由多辆相同或不同形式的机车车辆(以下统称车辆 )组成，以速度 V 通过线路；每节车体考虑浮沉、点头两个自由度，每个轮对考虑浮沉一个自由度；为简化计算，将具有二系悬挂或一系轴箱悬挂装置的车辆均简化成一系弹簧悬挂装置。此外，假设在行驶过程中车辆轮对始终与轨面保持密贴。对于轨道与路基，按常规方法将结构离散为有限元模型。将钢轨离散成梁单元(或四边形单元 )，胶垫或垫板、轨枕及以下介质包括路基和地基

23、均离散成四边形单元。由于轨道路基模型作为有限元模型，直接与车辆振动方程组合计算整个体系的动力响应，则计算工作量非常可观。因此，这里的钢轿路基模型按了结构法原理建立。由于结构的振动反应主要由最先几个低阶振型起控制作用，所以只需取前几阶振型进行计算，从而使计算工作量大大减少。为简明起见，通过仿真计算得出的“神州号”内燃动车组以160250 km/h 速度通过加固前后路涵过渡段时系统各种动力响应指标最大值汇总于表3、表 4，结论如下。(a)计算结果表明，当试验列车以200 km/ h 速度运行于京秦线被试路涵过渡段时，无论路基加固与否，能够满足舒适性要求以及路基强度要求。加固后的列车运行品质都要好于

24、未加固条件。(b 本次计算表明，无论什么地段，不管路基是否加固，路基应力水平都不高，即使在 250 km/ h 速度条件下也不会超限，因此不起控制作用。(c)当车速大于 200 km/ h 时，实测表明列车运行安全性和舒适性均受到影响，12尤其是动车的安全标准受到挑战，对提速起控制作用，必须考虑有效的路基加固措施。(d)路基所受压力随着深度的增加而迅速衰减，到一定深度时，加固与不加固条件下的动应力值差别很小，不必考虑提速对涵洞的结构受力影响。(e)从计算结果与实车试验结果比较可以看出，仿真计算是可行和可靠的，对实际工程具有参考指导意义。(f) 根据计算结果，路涵过渡段在车速小于 200km/

25、h 时，加固与不加固条件下各项动力性能指标差别很小，均能满足运行安全与舒适性要求，可不作全线加固，仅对个别特殊地段 (如路基病害段 )进行有效的加固处理。车速V> 200 km/ h 时，必须考虑有效的路基加固方式。无论提速与否，现有的涵洞结构都能满足使用要求。表 3 列车通过路涵过渡段时车辆运行品质计算与测试结果汇总列车速路基计 算 与动车响应拖车响应度情况测 试 结车体加速轮轨作用轮 重 减车体加速轮轨作用轮 重 减(km/h)果对比度 (m/s2)力 (kN)载率度 (m/s2)力 (kN)载率160加固前计算值2.42203.20.2770.858197.40.305加固后2.05196.50.2340.724189.60.253上行测试值1.910.331.140.51下行1.960.470.980.47180加