2018中考真题____三角函数综合应用专题复习

1、历届三角函数综合题中考真题训练1.（2017?贵阳）贵阳市某消防支队在一幢居民楼前进行消防演习，如图所示，消防官兵利用云梯 成功救出在C处的求救者后，发现在C处正上方17米的B处又有一名求救者，消防官兵立刻升高 云梯将其救出，已知点A与居民楼的水平距离是15米，且在A点测得第一次施救时云梯与水平线 的夹角/ CAD=60 ,求第二次施救时云梯与水平线的夹角/ BAD的度数（结果精确到1° ） .2. （2017?营口）如图，一艘船以每小时30海里的速度向北偏东750方向航行，在点A处测得码 头C在船的东北方向，航行40分钟后到达B处，这时码头C恰好在船的正北方向，在船不改变航 向的情

2、况下，求出船在航行过程中与码头 C的最近距离.（结果精确到海里，参考数据eA多情大3. （2017?黄冈）在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌 ABCD（如图所示），已知标语牌的高AB=5m在地面的点E处，测得标语牌点 A的仰角为30° ,在地面的点F处，测得标语牌点A的仰角为75° ,且点E, F, B, C在同一直线 上，求点E与点F之间的距离.（计算结果精确到米，参考数据： 血=,4. （2017?随州）风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片 组成（如图1）,图2是从图1引出的平面图.假设你站在 A处测得塔杆顶端C的仰角是5

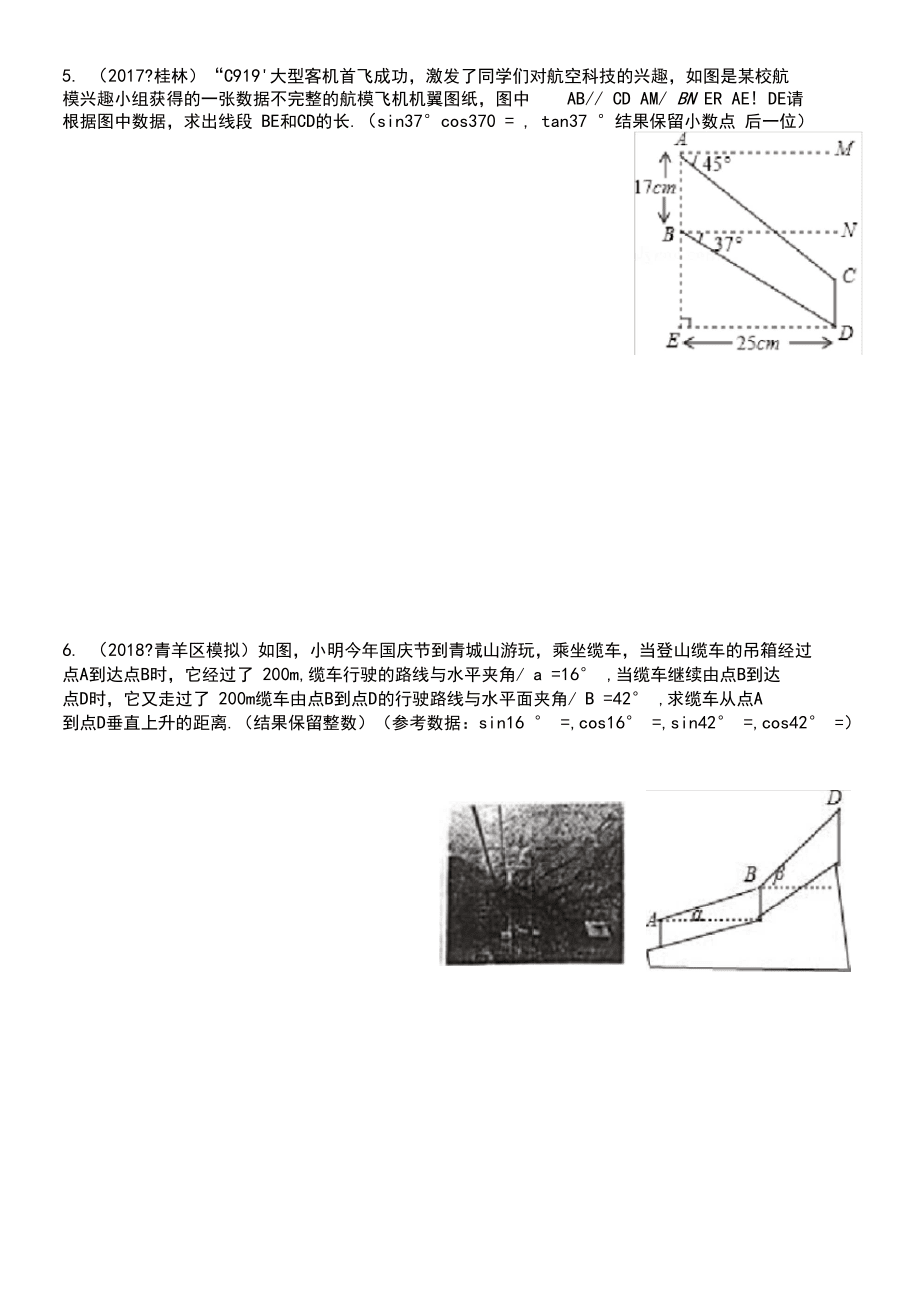
3、5。，沿 HA方向水平前进43米到达山底G处，在山顶B处发现正好一叶片到达最高位置，此时测得叶片的 顶端D （D G H在同一直线上）的仰角是45° .已知叶片的长度为35米（塔杆与叶片连接处的 长度忽略不计）,山高BG为10米,BGLHG CHLAH求塔杆 CH的高.（参考数据：tan55 ° tan35 ° ，sin55 ° ，sin35 ° ）5. （2017?桂林）“C919'大型客机首飞成功，激发了同学们对航空科技的兴趣，如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中AB/ CD AM/ BN ER AE!

4、 DE请根据图中数据，求出线段 BE和CD的长.（sin37°cos370 = , tan37 °结果保留小数点 后一位）6. （2018?青羊区模拟）如图，小明今年国庆节到青城山游玩，乘坐缆车，当登山缆车的吊箱经过点A到达点B时，它经过了 200m,缆车行驶的路线与水平夹角/ a =16° ,当缆车继续由点B到达 点D时，它又走过了 200m缆车由点B到点D的行驶路线与水平面夹角/ B =42° ,求缆车从点A 到点D垂直上升的距离.（结果保留整数）（参考数据：sin16 ° =,cos16° =,sin42° =,cos

5、42° =）7. （2017?呼和浩特）如图，地面上小山的两侧有 A, B两地，为了测量A, B两地的距离，让一 热气球从小山西侧 A地出发沿与AB成30°角的方向，以每分钟40m的速度直线飞行，10分钟后 到达C处，此时热气球上的人测得 CB与AB成70°角，请你用测得的数据求 A, B两地的距离AB 长.（结果用含非特殊角的三角函数和根式表示即可）8. （2017?张家界）位于张家界核心景区的贺龙铜像，是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图，在 RtABC中，/ ABC=,在RtzXDBC中，/ DBC=45 ,且CD= 米，求像体

6、AD的高度（最后结果精确到米，参考数据：。=,° =, ° =）Sa9. （2017?长春）如图，某商店营业大厅自动扶梯AB的倾斜角为31° , AB的长为12米，求大厅两层之间的距离BC的长.（结果精确到米）（参考数据：sin31 ° =, cos310 =, tan31 0 =）10 （2016?常德）南海是我国的南大门，如图所示，某天我国一艘海监执法船在南海海域正在进行常态化巡航，在A处测得北偏东30。方向上，距离为20海里的B处有一艘不明身份的船只正在向正东方向航行，便迅速沿北偏东 75。的方向前往监视巡查，经过一段时间后，在C处成功拦截不明船只

7、，问我海监执法船在前往监视巡查的过程中行驶了多少海里（最后结果保留整数）（参考数据：cos75° =, sin75 ° =, tan75 ° =, V3=, V2=）11. （2014?黔东南州）黔东南州某校九年级某班开展数学活动，小明和小军合作用一副三角板测 量学校的旗杆，小明站在 B点测得旗杆顶端E点的仰角为45。，小军站在点D测得旗杆顶端E点 的仰角为30° ,已知小明和小军相距（BD 6米，小明/高（AB）米，小军的身高（CD米， 求旗杆的高EF的长.（结果精确到，参考数据： 芯,V5-）F3 口12. （2012?黔东南州）如图，一艘货轮在 A

8、处发现其北偏东450方向有一海盗船，立即向位于正 东方向B处的海警舰发出求救信号，并向海警舰靠拢，海警舰立即沿正西方向对货轮实施救援， 此时距货轮200海里，并测得海盗船位于海警舰北偏西 600方向的C处.（1）求海盗船所在C处距货轮航线AB的距离.（2）若货轮以45海里/时的速度在A处沿正东方向海警舰靠拢，海盗以 50海里/时的速度由C处 沿正南方向对货轮进行拦截，问海警舰的速度应为多少时才能抢在海盗之前去救货轮（结果保留 根号）参考答案及分析1. （2017?贵阳）解：延长AD交BC所在直线于点E.由题意，得 BC=17米，AE=15米，Z CAE=60 , Z AEB=90 ,在 RtA

9、CE中，tan/CAE®,：CE=A? tan60 ° =15 心米.在 RtABE中，tan / BAE=l7"击, AE 15：/BAE« 71° .答：第二次施救时云梯与水平线的夹角/ BAD约为71° .【点评】本题考查了解直角三角形的应用，首先构造直角三角形，再运用三角函数的定义解题，构造出直 角三角形是解题的关键.2. （2017?营口）【分析】过点C作CELAB于点E,过点B作BDLAC于点D,由题意可知：船在航行过程中与码头C的最近距离是CE,根据/ DAB=30 , AB=20,从而可求出BD, AD的长度，进而可求

10、出 CE的长度.【解答】 解：过点C作CEL AB于点E,过点B作BDL AC于点D, 由题意可知：船在航行过程中与码头C的最近距离是CE,AB=30K =20,60vZ NAC=45 , / NAB=75 ,：/ DAB=30 ,：BD=AB=1Q2由勾股定理可知：AD=10.：；V BC/ AN：/ BCD=45 ,：CD=BD=1,0：AC=10. '+10vZ DAB=30 ,CE=-AC=5. -；+5内L-i答：船在航行过程中与码头 C的最近距离是海里【点评】本题考查解三角形的应用，解题的关键是熟练运用锐角三角函数以及勾股定理，本题属于中等题 型.3. （2017?黄冈）【

11、分析】 如图作FH!AE于H.由题意可知/ HAFh HFA=45 , 推出AH=HF设AH=HF=x WJ EF=2x, EH=lx, 在RtAEB中，由/ E=30° , AB=5米，推出 AE=2AB=1冰，可得x+Jlx=10,解方程即可.【解答】解：如图作 FHLAE于H.由题意可知/ HAFh HFA=45 , .AH=HF 设 AH=HF=x 则 EF=2x, EH应x, 在 RtAEB中，. /E=30° , AB=5米， ：AE=2AB=1眯， :x+ V3x=10, :x=5- 5,：EF=2x=10 石-10"米， 答：E与点F之间的距离为米

12、.【点评】本题考查解直角三角形的应用-仰角俯角问 题、锐角三角函数、等腰直角三角形的性质、一元一次方程等知识，解题的关键是学会添加常用辅助线， 构建方程解决问题.4. （2017?随州）【分析】 作 BE! DH 知 GH=BE BG=EH=10 设 AH=x,则 BE=GH=43+x 由 CH=AHtan CAH=tan55 ? x 知 CE=CH -EH=tan55° ? x-10,根据BE=DEh<W关于x的方程，解之可得. 【解答】解：如图，作BE!DH于点E,则 GH=BE BG=EH=10设 AH=x 贝U BE=GH=GA+AH=43+x在 RtACH中,CH=A

13、Htan CAH=tan55 ? x, ：CE=CH EH=tan55° ? xT0, vZ DBE=45 ,：BE=DE=CE+DCP 43+x=tan55° ? x - 10+35,解得：x=45,：CH=tan55 ? x=x 45=63, 答：塔杆CH的高为63米.【点评】本题考查了解直角三角形的应用，解答本题要求学生能借助仰角构造 直角三角形并解直角三角形.5. （2017?桂林）【分析】在R"BED中可先求得BE的长，过C作CF!AE于点F,则可求得AF的长，从而可求得 EF的长, 即可求得CD的长.【解答】解：V BN/ ED：/ NBDW BDE=

14、37 ,.AE1 DE：/E=90° ,：BE=DE tan / BD曰(cmj),如图，过C作AE的垂线，垂足为F,vZ FCAh CAM=45 ,：AF=FC=25c mV CD/ AE,四边形CDE助矩形，：CD=EF,. AE=AB+EB = cm),：CD=EF=AEAK ( cmi),答：线段BE的长约等于，线段 CD的长约等于.n25cm6. （2018?青羊区模拟）【分析】本题要求的实际是BC和DF的长度，已知了3的正切函数求出 BG DF的长.【解答】 解：RtABC中，斜边AB=200米，/ = =16AB BD者B是200米，可在RtABC和RtBFD中用a、B

15、C=AB sin a =200x sin16 ° =54 ( m),RtABDF 中，斜边 BD=200 米，Z 3 =42DF=BD? sin B =200x sin42 ° 内 132, 因此缆车垂直上升的距离应该是BC+DF=186口O【点评】本题主要考查解直角三角形的应用，利用条件构造直角三角形是解题的关键，注意角度的应用.答：缆车垂直上升了 186米.【点评】本题考查了解直角三角形的应用-坡度坡角问题，锐角三角函数的定义，结合图形理解题意是解决问题的关键.7. （2017?呼和浩特）【分析】 过点C作CML AB交AB延长线于点 M通过解直角 ACM得到AM的长度

16、，通过解直角 BCM得到BM的长度，则AB=AMb BM【解答】 解：过点C作CML AB交AB延长线于点 M 由题意得：AC=4（X 10=400 （米）.在直角 ACM 中，V Z A=30° ,：CMAC=200米,AM=AC=200/米.22在直角 4BCM 中，V tan20° =CM：BM=200tan20 ,：AB=AM BM=200/3-200tan20° =200 （右-tan20° ）,因此A, B两地的距离 AB长为200（V3 - tan20 ° ）米.【点评】本题考查解直角三角形的应用、三角函数等知识，解题的关键是添加

17、辅助线，构造直角三角形, 记住三角函数的定义，以及特殊三角形的边角关系，属于中考常考题型.8. （2017?张家界）【分析】根据等腰直角三角形的性质得出BC的长，再利用。二求出答案.Ba【解答】 解：二.在RtDBC中，/ DBC=45 ,且 CD冰, ：BC=.在 RtABC中，Z ABC=,：.° = =j-1LBC 2. 3 解得：AD-, 答：像体AD的高度约为.【点评】此题主要考查了解直角三角形的应用，正确掌握锐角三角函数关系是解题关键.9. （2017?长春）【分析】过B作地平面的垂线段 BC,垂足为C,构造直角三角形，利用正弦函数的定义，即可 求出BC的长.【解答】解：

18、过B作地平面的垂线段 BC垂足为C.在 RtABC中，V Z ACB=90 ,：BC=AH sin/BAC=12=（米）.即大厅两层之间的距离 BC的长约为米.【点评】本题考查了解直角三角形的应用-坡度坡角问题，把坡面与水平面的夹角a叫做坡角.在解决坡度的有关问题中，一般通过作高构成直角三角形，坡角即是一锐角，坡度实际就是一锐角的正切值，水平 宽度或铅直高度都是直角边，实质也是解直角三角形问题.10. （2016?常德）【分析】 过B作BDLAC在直角三角形 ABD中，利用勾股定理求出 BD与AD的长，在直角三角形 BCD中,求出CD的长，由AD+DCt出AC的长即可.【解答】解：过B作BDL

19、ACvZ BAC=75 - 30° =45° ,;在 RQABD中，/ BAD三 ABD=45 , A ADB=90 ,由勾股定理得：BD=AD=2x20=10衣(海里)，2在 RtBCD中，/ C=15 , C CBD=75 ,：tan/CBD,即 CD=10/x 二，BD则AC=AD+DC=0?+10<2X =67 (海里)，即我海监执法船在前往监视 的过程中行驶了 67海里.【点评】此题考查了解直角三角形的应用-方向角问题，熟练掌握直角三角形的性质是解本题的关键.11. （2014?黔东南州）【分析】过点A作AML EF于M,过点C作CNL EF于N,则MN=由小明站在B点测得旗杆顶端 E点的仰角 为45° ,可得 AEM是等腰直角三角形，继而得出得出 AM=ME设AM=ME=xm则CN= （x+6） m EN= （x-） m.在RtCEN中，由tan/ECN胃口,代入CN EN解方程求