函数的单调性与导数推荐（课堂PPT）

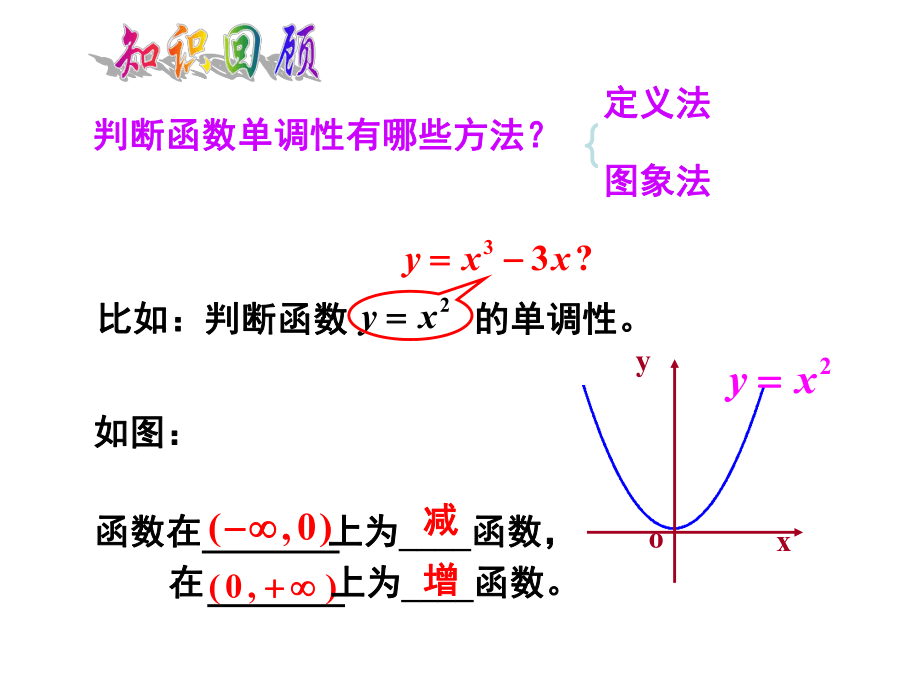
1、21理解函数单调性和导数的关系；理解函数单调性和导数的关系；2会利用导数判断函数的单调性。会利用导数判断函数的单调性。学习重点和难点学习重点和难点1重点：函数单调性和导数的关系重点：函数单调性和导数的关系2难点：函数单调性和导数的关系。难点：函数单调性和导数的关系。学习目标学习目标判断函数单调性有哪些方法？判断函数单调性有哪些方法？比如：判断函数比如：判断函数 的单调性。的单调性。yx 2 (,0) (0,)33 ?yxxxyo2yx 函数在函数在 上为上为_函数，函数，在在 上为上为_函数。函数。图象法图象法定义法定义法减减增增如图：如图：图象是单调上升的.01 y观察下列图象的单调区间,并

2、求单调区间相应的导数.02 xy02 xy图象是单调下降的.在x(-,0)内图象是单调上升的.在x( 0,+)内图象是单调上升的.)0(032时当 xxy012xy012xy图象是单调下降的.在x(-,0)内图象是单调下降的.在x( 0,+)内函数的单调性与其导函数正负的关系:当函数y=f (x)在某个区间内可导时，如果 , 则f (x)为增函数；如果 , 则f (x)为减函数。0)( xf0)( xf单调性单调性导数的正负导数的正负函数及图象函数及图象 (,0)在在上上递递减减 (0,)在在上上递递增增xyoyf x ( )abxyoyf x ( )ab切线斜率切线斜率 的正负的正负kxyo

3、2( )f xx a b( , )在在某某个个区区间间内内, ,fx ( )0f xa b( )( , )在在内内单单调调递递增增fx ( )0f xa b( )( , )在在内内单单调调递递减减注意：注意：应正确理解应正确理解 “ 某个区间某个区间 ” 的含义，的含义， 它必它必是定义域内的某个区间。是定义域内的某个区间。1 1应用导数求函数的单调区间应用导数求函数的单调区间(选填选填:“增增” ,“减减” ,“既不是增函数既不是增函数,也不是减函数也不是减函数”)(1) 函数函数y=x3在在3，5上为上为_函数。函数。 (2) 函数函数 y = x23x 在在2，+)上为上为_函数，函数，

4、 在在(,1上为上为_函数，在函数，在1,2上为上为_ _函数。函数。基础训练：基础训练：既不是增函数,也不是减函数求函数求函数 的单调区间。的单调区间。变变1：求函数求函数 的单调区间。的单调区间。3233yxx 233yxx 理解训练：理解训练：63yx 解解：110,022yxyx 令令得得 令令得得233yxx 1( ,)2 的单调递增区间为的单调递增区间为单调递减区间为单调递减区间为1(, )2 解解：2963 (32)yxxxx 2003yxx 令令得得或或2003yx 令令得得3233yxx 的单调递增区间为的单调递增区间为2(,0),( ,)3 例2、已知导函数 的下列信息：当

5、1x4,或x1时，当x=4,或x=1时，试画出函数f(x)图象的大致形状。)(xf 0)( xf0)( xf0)( xf41xyo)(xfy 解：由题意可知当1x4,或x0)(xf从而函数f(x)=x3+3x在xR上单调递增，见右图。(2) f(x)=x2-2x-3 ;解： =2x-2=2(x-1)0)(xf图象见右图。当 0，即x1时，函数单调递增；)(xf当 0，即x1时，函数单调递减；)(xf(3) f(x)=sinx-x ; x(0,p)解： =cosx-10)(xf当 0，即 时，函数单调递增；)(xf21712171xx或图象见右图。当 0，即 时，函数单调递减；21712171x

6、)(xf总结总结: 当遇到三次或三次以上的当遇到三次或三次以上的,或图象很难或图象很难画出的函数求单调性问题时，应考虑导数法。画出的函数求单调性问题时，应考虑导数法。求定义域求定义域求求( )fx令令()0()()0()fxfxfxfx 解解不不等等式式的的递递增增区区间间解解不不等等式式的的递递减减区区间间求定义域求定义域1 1什么情况下，用什么情况下，用“导数法导数法” 求函数单调性、求函数单调性、 单调区间较简便？单调区间较简便？2 2试总结用试总结用“导数法导数法” 求单调区间的步骤？求单调区间的步骤？cossin335(,)( ,2 )(,)(2 ,3 )22.2.2.yxxxABC

7、Dp pp pp pp pp pp pp pp p 函函数数在在下下面面哪哪个个区区间间内内是是增增函函数数( ( ) ) (04年全国理年全国理)Bp pp p( ,2 )该该函函数数在在上上为为增增函函数数。xxxxp pp p ( ,2 )sin0,sin0,如如图图, ,当当时时，yxxxxx cos(cos ) (sin )解解： xxxxxx cossinossincy 0即即：xyop pp p2p p3yx sinxyo12( )yf x xyo12( )yf x xyo1 2( )yf x xyo12( )yf x xyo( )yfx 2(A)(B)(C)(D)C设设 是函数是函数 的导函数，的导函数， 的图象如的图象如右图所示右图所示,则则 的图象最有可能的是的图象最有可能的是( )( )f x( )fx( )yfx ( )yf x 例3、如图，水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中，请分别找出与各容器对应的水的高度h与时间t的函数关系图象。 通过这堂课的研究，你明确了通过这堂课的研究，你明确了 ，你的收获与感受是你的收获与感受是 ，你存在的疑惑之处有你存在的疑惑之处有 。(课本课本) P98 A组组 1,2 322(