全等三角形的性质和判定教案

1、 中小学个性化课外辅导专家 卓尔教育教师教学辅导教案 编号： 授课教师日 期时 间 学 生年 级科 目课 题全等三角形的性质和判定 教学目标1理解全等三角形及其对应边、对应角的概念；能准确识别全等三角形的对应元素.2掌握全等三角形的性质；会用全等三角形的性质进行简单的推理和计算，解决某些实际问题.教学重难点三角形判定的应用课前检查上次作业完成情况：优 良 中 差 建议：_教 学 过 程【要点梳理】要点一、全等形形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.要点诠释：一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小都没有改变，即平移、翻折、旋转前后的图形全等

2、.两个全等形的周长相等，面积相等.要点二、全等三角形能够完全重合的两个三角形叫全等三角形.要点三、对应顶点，对应边，对应角1. 对应顶点，对应边，对应角定义两个全等三角形重合在一起，重合的顶点叫对应顶点，重合的边叫对应边，重合的角叫对应角.要点诠释：在写两个三角形全等时，通常把对应顶点的字母写在对应位置上，这样容易找出对应边、对应角.如以下图，ABC与DEF全等，记作ABCDEF，其中点A和点D，点B和点E，点C和点F是对应顶点；AB和DE，BC和EF，AC和DF是对应边；A和D，B和E，C和F是对应角.2. 找对应边、对应角的方法1全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边

3、；2全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角；3有公共边的，公共边是对应边； 4有公共角的，公共角是对应角；5有对顶角的，对顶角一定是对应角；6两个全等三角形中一对最长的边或最大的角是对应边或角，一对最短的边或最小的角是对应边或角，等等.要点四、全等三角形的性质全等三角形的对应边相等；全等三角形的对应角相等.要点诠释：全等三角形对应边上的高相等，对应边上的中线相等，周长相等，面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.【典型例题】类型一、全等形和全等三角形的概念1、以下每组中的两个图形，是全等图形的为 A B C D举一反三：【变式】如图，在5个条形方格图中

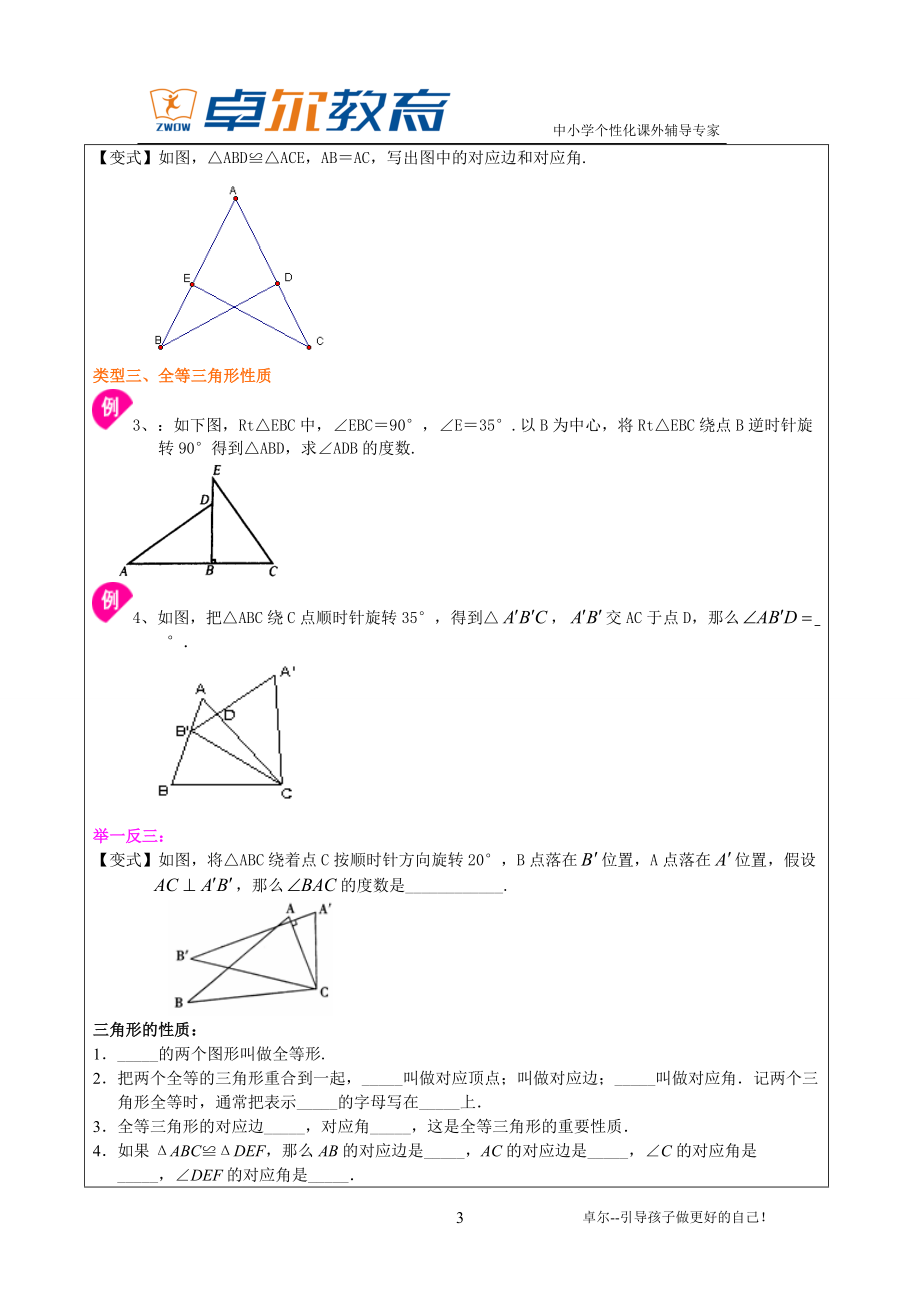
4、，图中由实线围成的图形与全等的有_.类型二、全等三角形的对应边，对应角2、如图，ABNACM，B和C是对应角，AB与AC是对应边，写出其他对应边和对应角. 【总结升华】全等三角形对应角所对的边是对应边；全等三角形对应边所对的角是对应角.举一反三：【变式】如图，ABDACE，ABAC，写出图中的对应边和对应角.类型三、全等三角形性质3、：如下图，RtEBC中，EBC90，E35.以B为中心，将RtEBC绕点B逆时针旋转90得到ABD，求ADB的度数.4、如图，把ABC绕C点顺时针旋转35，得到，交AC于点D，那么 举一反三：【变式】如图，将ABC绕着点C按顺时针方向旋转20，B点落在位置，A点落

5、在位置，假设，那么的度数是_.三角形的性质：1_的两个图形叫做全等形.2把两个全等的三角形重合到一起，_叫做对应顶点；叫做对应边；_叫做对应角记两个三角形全等时，通常把表示_的字母写在_上3全等三角形的对应边_，对应角_，这是全等三角形的重要性质4如果ABCDEF，那么AB的对应边是_，AC的对应边是_，C的对应角是_，DEF的对应角是_图115如图11所示，ABCDCB1假设D74DBC38，那么A_，ABC_2如果ACDB，请指出其他的对应边_；3如果AOBDOC，请指出所有的对应边_，对应角_图12 图136如图12，ABEDCE，AE2 cm，BE1.5 cm，A25，B48；那么DE

6、_cm，EC_cm，C_；D_7一个图形经过平移、翻折、旋转后，_变化了，但_都没有改变，即平移、翻折、旋转前后的图形二、选择题8：如图13，ABDCDB，假设ABCD，那么AB的对应边是 ADBBBCCCDDAD9以下命题中，真命题的个数是 全等三角形的周长相等 全等三角形的对应角相等全等三角形的面积相等 面积相等的两个三角形全等A4B3C2D110如图14，ABCBAD，A和B、C和D是对应顶点，如果AB5，BD6，AD4，那么BC等于 A6B5C4D无法确定 图1-4 图1-5 图1-611如图15，ABCAEF，假设ABC和AEF是对应角，那么EAC等于 AACBBCAFCBAFDBA

7、C12如图16，ABCADE，假设B80，C30，DAC35，那么EAC的度数为 A40B35C30D25、三、解答题13：如图17所示，以B为中心，将RtEBC绕B点逆时针旋转90得到ABD，假设E35，求ADB的度数图17图18图19综合、运用、诊断一、填空题14如图18，ABE和ADC是ABC分别沿着AB，AC翻折180形成的假设1232853，那么的度数为_15：如图19，ABCDEF，A85，B60，AB8，EH21求F的度数与DH的长；2求证：ABDE拓展、探究、思考16如图110，ABBC，ABEECD判断AE与DE的关系，并证明你的结论图110三角形全等的条件一、填空题1判断_

8、的_ 叫做证明三角形全等2全等三角形判定方法1“边边边即_指的是_3由全等三角形判定方法1“边边边可以得出：当三角形的三边长度一定时，这个三角形的_也就确定了4：如图21，RPQ中，RPRQ，M为PQ的中点求证：RM平分PRQ分析：要证RM平分PRQ，即PRM_，只要证_证明： M为PQ的中点， 图21_在_和_中，_ PRM_即RM5：如图22，ABDE，ACDF，BECF.求证：AD分析：要证AD，只要证_证明：BECF ，BC_在ABC和DEF中， 图22_ AD _6如图23，CEDE，EAEB，CADB，求证：ABCBAD证明：CEDE，EAEB，_， 图23即_在ABC和BAD中，

9、_，ABCBAD 综合、运用、诊断一、解答题7：如图24，ADBCACBD试证明：CADDBC. 图24图259“三月三，放风筝图26是小明制作的风筝，他根据DEDF，EHFH，不用度量，就知道DEHDFH请你用所学的知识证明 图26 三角形全等的判定1、如图1：ADBC，垂足为D，BD=CD。 求证：ABDACD。 2、AC=BD，AE=CF，BE=DF，证明：AECFACBDEF3、BE=CF，AB=CD， B=C.问AF=DE吗？ACDBEF4、，M是AB的中点，1=2，MC=MD，问C=D吗？说明理由。MABCD12ADEBC5、AD=AE，B=C，证明：AC=ABADBEC126、A

10、B=AC， 1=2，AD=AE，问ABDACE.说明理由。ACBDE7、AB与CD相交于点E，EA=EC，ED=EB，问AEDCEB吗？ACDEB8、如图，AD=BC，AE=BE，问C=D吗？9、如图：ABCD，B=D，求证：ADBC。DCFEAB10、AB=CD，BE=CF，AE=DF，问ABCD吗？11、如图：AD=AE，DAB=EAC，AM=AN。求证：AB=AC。ACDB123412、1=2，3=4，问AC=AD吗？说明理由。13、在ABC中，高AD与BE相交于点H，且AD=BD，问BHDACD，为什么？ABCEHD14、EFBC，AF=CD，ABBC，DEEF，问ABCDEF吗？说明

11、理由。ABCEDFABCDE1215、AD=AE，BD=CE，1=2，问ABDACE吗？ABCDO1216、1=2，BC=AD，问ABCBAD吗？17、如图，D，E，F，B在一条直线上，AB=CD，B=D，BF=DE，问(1)AE=CF(2)AECF。CDEFAB18、如图5：ABBD，EDBD，AB=CD，BC=DE。求证：AC垂直CE三角形 证明专项训练一1. ：如图 , 点A、C、B、D在同一条直线上 , AC=BD , AM=CN , BM=DN。求证：AMCN , BMDN 2. ：如图 , AB=AE , AC=AD , BC=DE , C , D在BE边上求证：CAE=DAB 3

12、. ：如图 , 四边形ABCD中 , ABCD , ADBC求证：ABDCDB 4. 如图, AB, CD, EF交于O点, 且AC=BD, ACDB.求证：O是EF的中点 5. ：如图 , ABBC于B , EFAC于G , DFBC于D , BC=DF求证：AC=EF 6. ：如图 , 1=2 , ABBC , ADDC , 垂足分别为B、D 求证：AB=AD三角形 证明专项训练二1、如图，求证： 2、如图,于点,于点,交于点,且.求证.3、如图，在ABC中,AB=CB,ABC=90,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:RtABERtCBF;(2)假设CAE=30,求ACF度数.ABCEF4、如图，点C是线段AB的中点，CE=C