第5章轴向拉伸和压缩

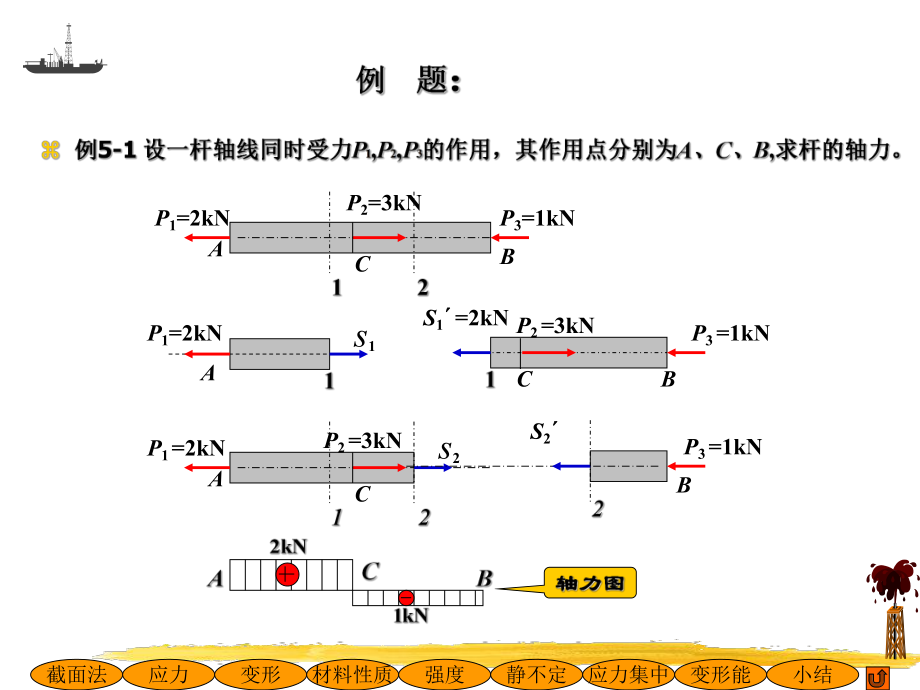
1、截面法应力变形材料性质强度静不定应力集中变形能小结 引言引言 工程中的轴向拉伸和压缩问题工程中的轴向拉伸和压缩问题截面法应力变形材料性质强度静不定应力集中变形能小结截面法应力变形材料性质强度静不定应力集中变形能小结PSPSX 00PSSPX 00离开截面为正，指向截面为负离开截面为正，指向截面为负 拉为正，压为负拉为正，压为负内力符号规定与静力学不同，是以变形的不同确内力符号规定与静力学不同，是以变形的不同确 定正负，截面上的未知内力皆用正向画出定正负，截面上的未知内力皆用正向画出截面法应力变形材料性质强度静不定应力集中变形能小结P1=2kNP1=2kNS1 =2kNP2=3kNP2 =3kN

2、P3=1kNAABCCs1s2P1 =2kNP2 =3kNACP3 =1kNBBS2 P3 =1kN截面法应力变形材料性质强度静不定应力集中变形能小结截面法应力变形材料性质强度静不定应力集中变形能小结：1、确定研究对象、确定研究对象： 吊钩和绳子吊钩和绳子 2、用截面法确定内力、用截面法确定内力 1）用截面取出研究对象）用截面取出研究对象 2）画出分离体受力图）画出分离体受力图 3）列平衡方程求出内力）列平衡方程求出内力:0 X21SS :0 Y030cos21001 S21kN78.5SS (a) PPP A=S=PAPAS 轴向拉伸或压缩时横截面上轴向拉伸或压缩时横截面上应力计算式应力计算

3、式 是垂直于横截面的应力是垂直于横截面的应力-正应力正应力轴力为拉力时为轴力为拉力时为拉应力拉应力轴力为压力时为轴力为压力时为压应力（压应力（可用可用负号表示）负号表示） 1、应力的概念、应力的概念2、用三大关系推导计算公式、用三大关系推导计算公式 Ell 纵向线应变截面法应力变形材料性质强度静不定应力集中变形能小结 在最小截面处应用截面法：在最小截面处应用截面法：截取分离体，在截面上画上内截取分离体，在截面上画上内力，力，画画出分离体的受力图，利出分离体的受力图，利用平衡方程或向截面简化求出用平衡方程或向截面简化求出内力内力:0 YkN800 PSMPa2087014. 3108004423

4、2minmax dSAS 解：解：1、计算轴力，画轴力图、计算轴力，画轴力图轴力图轴力图0 PS2、用最小横截面面积计算最大压缩应力、用最小横截面面积计算最大压缩应力截面法应力变形材料性质强度静不定应力集中变形能小结 AS SA AS nu 将构件的工作应力限制在极限应力将构件的工作应力限制在极限应力的范围内还是不够的，因为：的范围内还是不够的，因为： （1）主观设定的条件与客观实际）主观设定的条件与客观实际之间还存在差距。之间还存在差距。 （2）构件需有必要的强度储备。）构件需有必要的强度储备。将材料的破坏应力打一个折扣，即将材料的破坏应力打一个折扣，即除以一个大于除以一个大于1的系数的系数

5、n后，作为构后，作为构件应力所不允许超过的数值。称为件应力所不允许超过的数值。称为许用应力。以许用应力。以 表示，这个系数表示，这个系数n称为称为。以材料的屈服点与抗拉强度之比为以材料的屈服点与抗拉强度之比为依据来选取极限应力和安全系数。依据来选取极限应力和安全系数。比值比值称为称为bs 对于轴向拉伸和压缩的杆件应满足的条对于轴向拉伸和压缩的杆件应满足的条件是：件是：这是轴向拉伸和压缩时的强度条件。这是轴向拉伸和压缩时的强度条件。解决工程实际中有关构件强度的问题：解决工程实际中有关构件强度的问题：（1）强度校核）强度校核（2）选择截面）选择截面（3）确定许用载荷）确定许用载荷破坏应力破坏应力或

6、或s b 截面法应力变形材料性质强度静不定应力集中变形能小结（确定研究对象，（确定研究对象， 用截面截取对象，画受力图用截面截取对象，画受力图0)(sin:0 QGSYBC sinQGSBC 得得又由三角关系知：又由三角关系知：352. 045 . 15 . 1sin22BCACll 代入上式得：代入上式得：KN8 .56352. 0155BCS截面法应力变形材料性质强度静不定应力集中变形能小结（2）选择截面尺寸选择截面尺寸 由式（由式（1-10），）， 拉杆横截面面积应为：拉杆横截面面积应为： 2mm40614010008 .56 BCSA注意：注意：2N/mm1MPa1 的换算关系。的换算

7、关系。又因又因42dA 故拉杆直径为故拉杆直径为mm8 .2214. 34064d最后可选用最后可选用d=25mm的圆钢。的圆钢。截面法应力变形材料性质强度静不定应力集中变形能小结：（：（1）计算侧臂轴力计算侧臂轴力 截取节点截取节点A为研究对象为研究对象 可设两杆轴力皆为可设两杆轴力皆为 ，受受力分析如图。力分析如图。 0cos2, 0 SPY得得 cos2PS 式中式中92. 0420960960cos22 再由平衡方程再由平衡方程截面法应力变形材料性质强度静不定应力集中变形能小结代入上式得代入上式得PPS544. 092. 02(2)求许用载荷求许用载荷 AS 即即1.27MNN1270

8、00080544. 0)36120(21080)1036120(2544. 066 PP故按侧杆强度，吊环的许用载荷为故按侧杆强度，吊环的许用载荷为1.27MN。截面法应力变形材料性质强度静不定应力集中变形能小结PllllEAPll EASll 或或ll 将（将（1-2）改写为）改写为ASEll 1E P（5-2） bbaaE El iiiiiAElSllbbbaaa,abab截面法应力变形材料性质强度静不定应力集中变形能小结截面法应力变形材料性质强度静不定应力集中变形能小结 E（3）材料恢复抵抗变形的能力，要使它继材料恢复抵抗变形的能力，要使它继续变形，必须增加应力，称为材料的续变形，必须增

9、加应力，称为材料的强化。弹性变形和塑性变形共存强化。弹性变形和塑性变形共存p 比例极限比例极限s 屈服极限屈服极限b 强度极限强度极限E （2）应力几乎不变，应变不断应力几乎不变，应变不断增加，产生明显的塑性变增加，产生明显的塑性变形的现象，称为屈服现象形的现象，称为屈服现象 截面法应力变形材料性质强度静不定应力集中变形能小结混凝土梁混凝土梁钢筋钢筋自增强厚壁圆自增强厚壁圆筒中的塑性区筒中的塑性区残余周向应力残余周向应力沿壁厚分布情况沿壁厚分布情况自增强后受内压时自增强后受内压时周向应力周向应力沿壁厚分布情况沿壁厚分布情况截面法应力变形材料性质强度静不定应力集中变形能小结%100001 lll

10、n %100010 AAA 和和越大，说明材料塑性越高越大，说明材料塑性越高脆性材料脆性材料塑性材料塑性材料%5 n %5 n 局部变形阶段局部变形阶段应应力力 应变应变截面法应力变形材料性质强度静不定应力集中变形能小结2 . 0 截面法应力变形材料性质强度静不定应力集中变形能小结两条曲线的主要部分基本重合，两条曲线的主要部分基本重合，因此低碳钢压缩时的弹性模量、因此低碳钢压缩时的弹性模量、屈服点等都与拉伸试验的结果基屈服点等都与拉伸试验的结果基本相同。本相同。低碳钢拉伸低碳钢拉伸低碳钢压缩低碳钢压缩截面法应力变形材料性质强度静不定应力集中变形能小结截面法应力变形材料性质强度静不定应力集中变形

11、能小结截面法应力变形材料性质强度静不定应力集中变形能小结截面法应力变形材料性质强度静不定应力集中变形能小结截面法应力变形材料性质强度静不定应力集中变形能小结 能用静力学平衡能用静力学平衡方程求解的问题，称方程求解的问题，称为为静定问题静定问题。 未知力多于平衡未知力多于平衡方程，用静力学平衡方程，用静力学平衡方程不能求解的问题方程不能求解的问题，称为静不定问题称为静不定问题截面法应力变形材料性质强度静不定应力集中变形能小结,221alal,221ll这就是各杆应满足的这就是各杆应满足的变形几何条件变形几何条件。求静不定问题应考虑求静不定问题应考虑三个方面三个方面关系：关系：（1）静力学平衡关系

12、）静力学平衡关系（2）变形几何关系）变形几何关系（3）变形与力之间的物理关系）变形与力之间的物理关系1l2l设两杆的伸长变形为设两杆的伸长变形为 和和2221112AElSAElS截面法应力变形材料性质强度静不定应力集中变形能小结解解:（1）列静力学方程列静力学方程 解除约束，解除约束，设约束反力为设约束反力为RA.RB.列方程：列方程：0, 0 PRRYBA（2）列变形几何条件列变形几何条件 设杆设杆受力受力P作用后作用后,C点移至点移至 C，在，在原有约束条件下，杆原有约束条件下，杆AB的长度的长度不不变变，故此，故此时时AC段的伸长段的伸长lAC 与与CB段的缩短段的缩短lCB 应该相等

13、。应该相等。由此变形几何条件：由此变形几何条件： lllCBAC（b）截面法应力变形材料性质强度静不定应力集中变形能小结（3） 列物理条件列物理条件 由虎克定律：由虎克定律：EAaRlEAaRlBCBAAC 2（4） 建立补充方程，解出约束反力建立补充方程，解出约束反力将式（将式（c）代如式（代如式（b），），得补充方程得补充方程EAaREAaRBA2即即BARR 2联立方程得：联立方程得：32,3PRPRBA （c）截面法应力变形材料性质强度静不定应力集中变形能小结例例1-9 杆杆AB长为长为l , ,面积为面积为A , ,材料的材料的弹性模量弹性模量E和线膨胀系数和线膨胀系数 , ,求温度

14、求温度升高升高 T 后杆温度应力。后杆温度应力。 解除约束，设约解除约束，设约束反力为束反力为RA.RB.列方程：列方程：0, 0 BARRXTl Rl RTll 因温度引起的伸长因温度引起的伸长因轴向压力引起的缩短因轴向压力引起的缩短lTlT EARllT EARllR TEAR TEAR RRRBA :得得截面法应力变形材料性质强度静不定应力集中变形能小结(a)为钢板横截面的为钢板横截面的温度分布情况温度分布情况(b)焊后的变形情况焊后的变形情况和残余应力和残余应力为防止管道温度应力过大顶坏两端装置为防止管道温度应力过大顶坏两端装置而接入管道的伸缩节而接入管道的伸缩节截面法应力变形材料性质强度静不定应力集中变形能小结m maxASm ASA 0lim 横截面上的最大应力横截面上的最大应力 max与平均应力与平均应力 m 的比值称为的比值称为应力集中系数应力集中系数，以，以 表示。表示。当当 A 趋于零时，则此比值的极限趋于零时，则此比值的极限一点应力一点应力的定义：的定义：微面积上的平均应力为微面积上的平均应力为截面法应力变形材料性质强度静不定应力集中变形能小结lPW21lPU21lSU21拉拉杆杆变变形形能能计计算算式式EAlSU22 2121 AllSu)( ldPdW lldPW0)(EEAlSAlu22122 截面法应力变形材料性质强度静不定应力集中变形能小结2 P