结构力学章节习题及参考答案

1、第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1是非判断题(1)若平面体系的实际自由度为零，则该体系一定为几何不变体系。()(2)若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。()(3)若平面体系的计算自由度WV0,则该体系为有多余约束的几何不变体系。()(4)由三个较两两相连的三刚片组成几何不变体系且无多余约束。()(5)习题2.1(5)图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。()习题2.1(5)图(6)习题2.1(6)(a)图所示体系去掉二元体ABC后,几何可变体系。()成为习题2.1(6)(b)图，故原

2、体系是(7)习题2.1(6)(a)图所示体系去掉二元体EDF后,几何可变体系。()成为习题2.1(6)(c)图，故原体系是(a)(b)习题2.1(6)图习题2.2填空(1)习题2.2(1)图所示体系为习题2.2(1)图(2)习题2.2(2)图所示体系为体系。习题2-2(2)图(3)习题2.2(3)图所示4个体系的多余约束数目分别为zxDOo习题2.2(3)图(4)习题2.2(4)图所示体系的多余约束个数为Q森露薪麴襄愿习题2.2(4)图(6)习题2.2(6)图所示体系为体系，有个多余约束。习题2.2(6)图(7)习题2.2(7)图所示体系为体系，有个多余约束。习题2.2(7)图习题2.3对习题

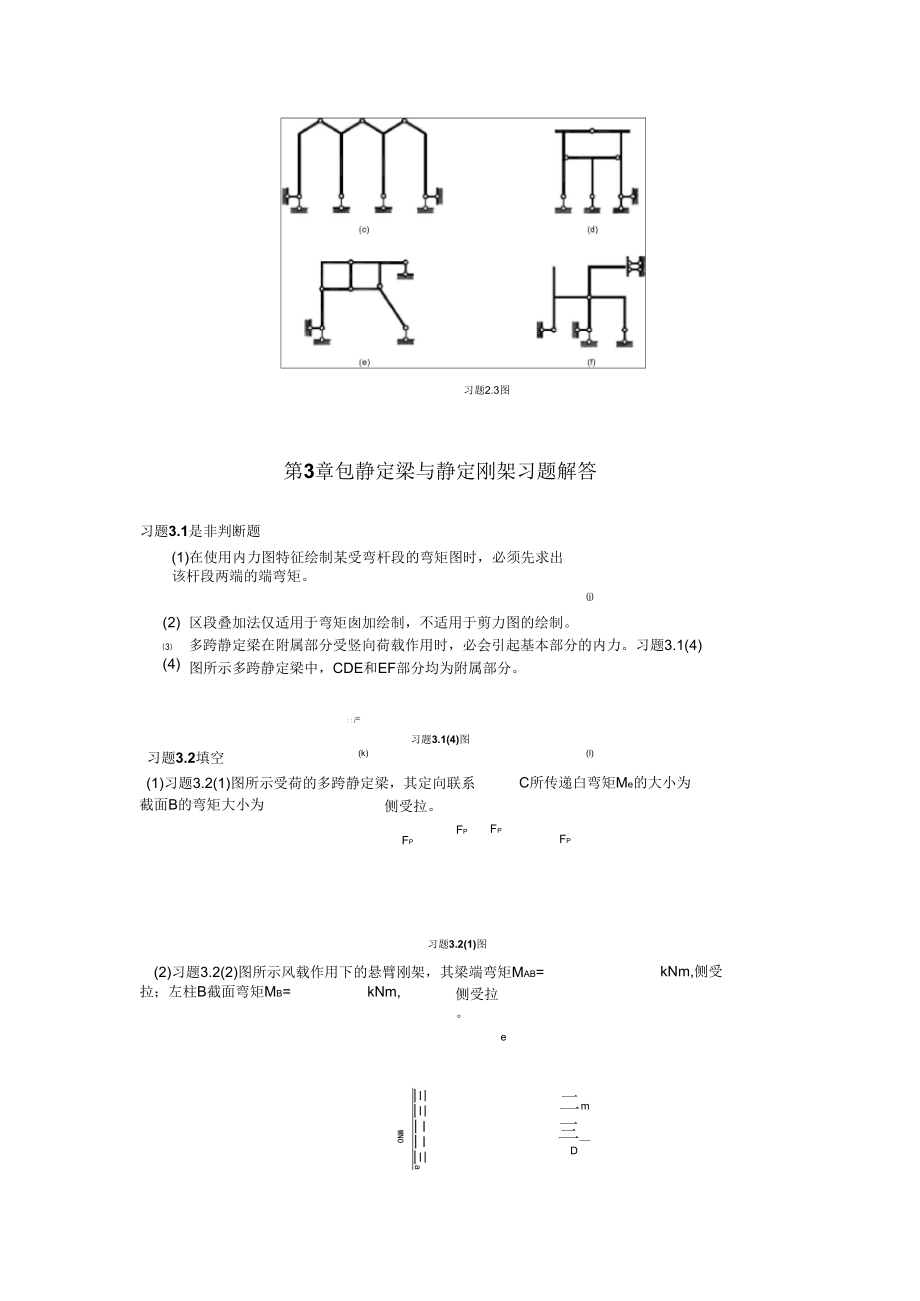
3、2.3图所示各体系进行几何组成分析。(a)(b)习题2.3图第3章包静定梁与静定刚架习题解答习题3.1是非判断题(j)(1)在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。(2)(4)区段叠加法仅适用于弯矩囱加绘制，不适用于剪力图的绘制。多跨静定梁在附属部分受竖向荷载作用时，必会引起基本部分的内力。习题3.1(4)图所示多跨静定梁中，CDE和EF部分均为附属部分。:产习题3.1(4)图习题3.2填空(k)(l)(1)习题3.2(1)图所示受荷的多跨静定梁，其定向联系C所传递白弯矩Me的大小为截面B的弯矩大小为侧受拉。FpFpFpFpkNm,侧受习题3.2(1)图(2)习

4、题3.2(2)图所示风载作用下的悬臂刚架，其梁端弯矩Mab=拉；左柱B截面弯矩Mb=kNm,侧受拉。e三三二二三aWNO二m三_Dm6m习题3.3作习题3.3图所示单跨静定梁的M图和Fq图。(b)a(e)习题3.4作习题3.4图所示单跨静定梁的内力图。(c)习题3.4图习题3.5作习题3.5图所示斜梁的内力图。5kN/m习题3.6作习题3.6图所示多跨梁的内力图。)6kN2kN/mDAEBCL2ml3mI3m3m(a)习题3.6图(a)习题3.7改正习题3.7图所示刚架的弯矩图中的错误部分。(a)(c)习题3.7图(f)6kN习题3.8作习题3.8图所示刚架的内力图。BX-m4m4m(b)习题

5、3.8图第4章静定拱习题解答习题4.1是非判断题(1)三校拱的水平推力不仅与三个校的位置有关，还与拱轴线的形状有关。()(2)所谓合理拱轴线，是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。()(3)改变荷载值的大小，三较拱的合理拱轴线形状也将发生改变。()习题4.2填空(1)习题3.2(3)图所示三校拱的水平推力Fh等于习题4.3求习题3.154f、y=yx(l-x)。习题3.2(3)图图所示三校拱支反力和指定截面K的内力。已知轴线方程第5章静定平面桁架习题解答习题5.1是非判断题(1)利用结点法求解桁架结构时，可从任意结点开始。()习题5.2填空(1)习题3.2(4)图所示桁架中有根零杆

6、。习题5.3试用结点法求习题3.10图所示桁架杆件的轴力。习题3.10图习题3.11图习题5.5用截面法求解习题3.12图所示桁架指定杆件的轴力。Fp(b)Im第6章结构的位移计算习题解答习题6.1是非判断题(1)变形体虚功原理仅适用于弹性体系，不适用于非弹性体系。()(2)虚功原理中的力状态和位移状态都是虚设的。()(3)功的互等定理仅适用于线弹性体系，不适用于非线弹性体系。()(4)反力互等定理仅适用于超静定结构，不适用于静定结构。()(5)对于静定结构，有变形就一定有内力。()(6)对于静定结构，有位移就一定有变形。()(7)习题4.1(7)图所示体系中各杆EA相同，则两图中C点的水平位

7、移相等。()(8) Mp图，M图如习题4.1(8)图所示，EI=常数。下列图乘结果是正确的:,1(2支EI38(9) Mp图、M图如习题4.1(9)图所示，下列图乘结果是正确的:11(Ay01A2y02)A3y03EI1EI2(10)习题4.1(10)图所示结构的两个平衡状态中，有一个为温度变化，此时功的互等定理不成立。()(a)(b)习题4.1(7)图111JIJ-JJIJIJ11JmJiHI(a)Mp图(b)M图1l/4(b)M图习题4.1(8)图(a)习题4.1(9)图ti(b)习题4.1(10)图习题6.2填空题(1)习题4.2(1)图所示刚架，由于支座B下沉所引起D点的水平位移Adh

8、=,(2)虚功原理有两种不同的应用形式，即原理和原理。其中，用于求位移的是原理。(3)用单位荷载法计算位移时，虚拟状态中所加的荷载应是与所求广义位移相应的(4)图乘法的应用条件是：且Mp与环图中至少有一个为直线图形。(5)已知刚架在荷载作用下的Mp图如习题4.2(5)图所示，曲线为二次抛物线，横梁的抗弯刚度为2EI,竖杆为EI,则横梁中点K的竖向位移为(6)习题4.2(6)图所示拱中拉杆AB比原设计长度短了1.5cm,由此引起C点的竖向位移为;引起支座A的水平反力为习题4.2(7)图所示结构，当C点有Fp=1(J)作用时，D点竖向位移等于(T),当E点有图示荷载作用时，C点的竖向位移为(8)习

9、题4.2(8)图(a)所示连续梁支座B的反力为Frb=卫()，则该连续梁在支座16下沉4=1时(如图(b)所示)，D点的竖向位移3m3m习题4.2(6)图习题4.2(5)图习题4.2(7)图(b)习题4.2(8)图习题6.3分别用积分法和图乘法求习题4.3图所示各指定位移Acv。EI为常数。1)求&V(a)2)求&vxCBxFp=1CFplA1l4P4(b)Mp图(c)M图习题4.3(1)图20kN/m'ACEIb2m,卜2m.(a)16021040ACBAx(b)MP图(kNm)1Cx(c)M图习题4.3(2)图3)求&v(a)Bxx8"24&quo

10、t;2A4)求名Bx1x2q噂A"""2EF"E""EI"/)M图2lIl(b)MP图习题4.3(3)图1Cql/2ql2,2ql/81/3(a)(b)MP图(c)m图习题4.3(4)图习题6.4分别用积分法和图乘法求习题4.4(a)图所示刚架C点的水平位移%已知EI=常数。x(b)Mp图(c)M"图(a)ql2习题4.4图习题6.5习题4.5(a)图所示桁架各杆截面均为A=2X10E=2.1X108kN/m2,FP=30kN,d=2m。试求C点的竖向位移。2Fp-3FPFPC2Fp(b)FNP图E%FPBD习题&

11、#165;A一第7章4.5用E2/2B为法可题解答12d12d-v_1_V2d1d(C)Fn图12d(d)Fn图习题7.1是非判断题(1)习题5.1(1)图所示结构，当支座A发生转动时，各杆均产生内力。+tiC+t；cc11+习题5.1(1)图习题5.1(2)图(2)习题5.1(2)图所示结构，当内外侧均升高tc时，两杆均只产生轴力。(3)习题5.1(3)图(a)和(b)所示两结构的内力相同。(a)q(b)习题5.1(3)图(4)习题5.1(3)图(a)和(b)所示两结构的变形相同。习题7.2填空题(1)习题5.2(1)图(a)所示超静定梁的支座A发生转角仇若选图(b)所示力法基本结构,则力法

12、方程为，代表的位移条件是，其中，1c若选图(c)所示力法基本结构时，力法方程为,代表的位移条件是,其中&c二(b)习题5.2(1)图.XiA丫一(c)(2)习题5.2(2)图(a)所示超静定结构，当基本体系为图(b)时，力法方程为L1P=；当基本体为图(C)时，力法方程为,；：1P=TTHJlinnTIEIEIqX1(b)(c)(a)习题5.2(2)图(3)习题5.2(3)图(a)所示结构各杆刚度相同且为常数,AB杆中点弯矩为侧受拉；图(b)所示结构Mbc=侧受拉。q(b)qa(a)2EIEIEI(4)连续梁受荷载作用时，其弯矩图如习题5.2(4)图所示，则D点的挠度为位移方向为习题习

13、题习题7.37.47.5试确定习题5.3图所示结构的超静定次数。(a)(c)用力法计算习题用力法计算习题EI=常数(b)习题5.3图5.4图所示各超静定梁，并作出弯矩图和剪力图。4kN/m|Alir.IL|.,r,jBEI8kN；-CEIIFpC2EIEIEI6ml/2(1)习题5.4图5.5图所示各超静定刚架，并作出内力图。EI=常数4m4m习题5.5图习题7.6利用对称性，计算习题5.12图所示各结构的内力，并绘弯矩图。EI=常数习题5.12图习题7.7画出习题5.17图所示各结构弯矩图的大致形状。已知各杆EI=常数。(a)习题8.1确定用位移法计算习题(除注明者外，其余杆的EI月常数。)

14、EAi(a)习题8.2是非判断(1)(2)(3)结构。(4)位移法习题解答6.1图所示结构的基本未知量数目,(e)位移法基本未知量的个数与结构的超静定次数无关。位移法可用于求解静定结构的内力。(c)并绘出基本结构。(f)用位移法计算结构由于支座移动引起的内力时，采用与荷载作用时相同的基本()位移法只能用于求解连续梁和刚架，不能用于求解桁架。习题8.3用位移法计算习题6.6图所示连续梁，作弯矩图和剪力图,)EI=常数。12kN/m15kNMa8kNmc32kNB4mI6m2m4m-4m12ml2m习题6.6图习题8.4用位移法计算习题6.7图所示结构，作弯矩图，EI=常数。6kN/mBEIEI6

15、kNCrm£1=常数4m2m2m(1)习题6.7图lFp第9章渐近法习题解答习题9.1是非判断题力矩分配法可以计算任何超静定刚架的内力。(2)习题7.1(2)图所示连续梁的弯曲刚度为EI,杆长为l,杆端弯矩Mbc<0.5M°()习题7.1(3)图习题7.1(2)图习题7.1(3)图所示连续梁的线刚度为i,欲使A端发生顺时针单位转角，需施加的力矩Ma>3L()习题9.2填空题(1)习题7.2(1)图所示刚架EI=常数，各杆长为l,杆端弯矩Mab=。(2)习题7.2(2)图所示刚架EI=常数，各杆长为l,杆端弯矩Mab=。(3)习题7.2(3)图所示刚架各杆的线刚度

16、为i,欲使结点B产生顺时针的单位转角,应在结点B施加的力矩Mb=。40kN2EI3m3m14kN-m习题7.2(1)图(4)用力矩分配法计算习题Cbc=20kN-m习题7.2(2)图7.2(4)图所示结构(EI=常数)MbMb-CC习题7.2(3)图时，传递系数Cba=习题9.3用力矩分配法计算习题7.3图所示连续梁，作弯矩图和剪力图，并求支座的反力。(2)习题7.3图习题9.4用力矩分配法计算习题7.4图所示连续梁，作弯矩图。36kN12kN/m40kNA-r24kN/m2EIB-1.5EICEID川川Hl4m2m6m6m2EIB4m|2m日C|2mEI(2)习题7.4图EIEL习题9.5用

17、力矩分配法计算习题7.5图所示刚架，作弯矩图。60kN8kN/m15kN/m2m2m“I”山-2E1EI3m(1)30kwmnni7in20kN/mAEIB20kN2EIDCEI=常数44mJ3mm3mm12m(2)4m2m,此三圜黑此修改此二图照此谬改5m200kNm£1=常数50kNm5m2m习题7.5图第11章影响线及其应用习题解答习题11.1是非判断题(1)习题8.1(1)图示结构BC杆轴力的影响线应画在BC杆上。()上C上Fqc影响线()(b)习题8.1(2)图(2)习题8.1(2)图示梁的Me影响线、Fqc影响线的形状如图(a)、(b)所示。(3)习题8.1(3)图示结构

18、，利用Me影响线求固定荷载Fp1、Fp2、Fp3作用下Me的值,可用它们的合力Fr来代替，即Me=Fp1Y1+Fp2y2+Fp3y3=Fr?。()习题8.1(3)图(4)习题8.1(4)图中的(a)所示主梁Fqc左的影响线如图(b)所示。()习题8.1(4)图(5)习题8.1(5)图示梁Fra的影响线与Fqa右的影响线相同。(习题8.1(5)图(6)简支梁的弯矩包络图为活载作用下各截面最大弯矩的连线。习题11.2填空题(1)用静力法作影响线时，其影响线方程是。用机动法作静定结构的影响线，其形状为机构的。(2)弯矩影响线竖标的量纲是。(3)习题8.2(3)图所示结构，Fp=1沿AB移动，Md的影

19、响线在B点的竖标为Fqd的影响线在B点的竖标为习题8.2(3)图(4)习题8.2(4)图所示结构，Fp=1沿ABC移动，则Md影响线在B点的竖标为习题8.2(4)图C点的竖习题8.2(5)图(5)习题8.2(5)图所示结构，Fp=1沿AC移动，截面B的轴力Fnb的影响线在标为。习题11.3单项选择题(1)习题8.3(1)图所示结构中支座A右侧截面剪力影响线的形状为()。习题8.3(1)图(2)习题8.3(2)图所示梁在行列荷载作用下，反力Fra的最大值为()。(a)55kN(b)50kN(c)75kN(d)90kN习题8.3(2)图(b)(d)BC,CD均为零；BC不为零，CD为零。习题8.3

20、(3)图所示结构Fqc影响线(Fp=1在BE上移动)BC、CD段竖标为()(a)BC,CD均不为零；(c)BC为零，CD不为零;Fp=1(4)习题8.3(4)图所示结构中，支座习题8.3(3)图B左侧截面剪力影响线形状为(5)习题(a)8.3(5)图所示梁在行列荷载作用下，截面K的最大弯矩为15kNm(b)35kNm(c)5kN5kN5kN4m14ml30kNm(d)42.5kNm12mKr4m习题11.4作习题8.4(a)图所:习题8.3(5)图不悬臂梁Fra、Mc、CFqc的影响线。Im4m(a)Fra1习题8.4图习题11.5作习题8.5(a)图所示结构中Fnbc、Md的画梭影响Fp=1

21、在AE上移动。(c)Mc影响线31.2m_2m_2m(a)习题8.5图325(b)Fnbc影响线2m2m4mBj_(c)M影响线-1习题11.6作习题8.6(a)图所示伸臂梁的Ma、Me、Fqa左、Fqa右的影响线。Fp=1(a)习题8.6图(b)MA影响线习题11.7作习题8.7(a2图所示结构中截面C的Me、Fqc的影响线。(Fp=4/3Me影响线CBd)Fqa影响线1(a)习题8.7图1/33m0.5AE.2m.5-6m(a)4r3m-0.5D工(C)Fqc影响线3m2m111/8习题19.15图(e)IFOC懒狗线习题11.8用机动法作习题8.13(a)图所示静定多跨梁的Frb、Me、

22、Fqb左、Fqb右、Fqc的影响线。0.5a(b)FRB影响线3/81.51/2(c)Me影响线习题11.9利用影响线，求习题8.14(a)图所不固定荷载作用正截面K的内力Mk和Fqk左。150kN150kNKJ-30kN/m3/41/4(d)FQB左影响线2m2m|2m2m(a)14m旦81m1习题8.14图习题11.10用机动法作习题8.1省3a)图所示连续梁Mk、(e)Fqb右影响线2Mb、Fqb左、Fqb右影响线的形状。若梁上有随意布置的均布活荷载，请画出使截面分置。CK4/3D工二1/3工工2/31/3习题8.16图2/3斗(a)l/l2(c)Fq侬影响线(b)MK影响线(C)MKm

23、ax载荷布置Fq旺影响线第2章平面体系的机动分析习题解答习题2.1是非判断题(1)若平面体系的实际自由度为零，则该体系一定为几何不变体系。()(2)若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。()(3)若平面体系的计算自由度WV0,则该体系为有多余约束的几何不变体系。()(4)由三个较两两相连的三刚片组成几何不变体系且无多余约束。()(5)习题2.1(5)图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。()习题2.1(5)图(6)习题2.1(6)(a)图所示体系去掉二元体ABC后,几何可变体系。()成为习题2.1(6)(b)图，

24、故原体系是习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6)(c)图，故原体系是几何可变体系。()【解】(1)(2)(3)(4)(5)(6)错误。错误。错误。错误。错误。(b)习题2.1(6)图正确。WE0是使体系成为几何不变的必要条件而非充分条件。只有当三个较不共线时，该题的结论才是正确的。CEF不是二兀体。ABC不是二元体。EDF不是二兀体。习题2.2填空(1)习题2.2(1)图所示体系为体系。习题2.2(1)图(2)习题2.2(2)图所示体系为体系。习题2-2(2)图(3)习题2.2(3)图所示4个体系的多余约束数目分别为zDOo习题2.2(3)图(4)习题2.2(

25、4)图所示体系的多余约束个数为习题2.2(4)图(5)习题2.2(5)图所示体系的多余约束个数为习题2.2(5)图(6)习题2.2(6)图所示体系为体系，有个多余约束。习题2.2(6)图(7)习题2.2(7)图所示体系为体系，有个多余约束。习题2.2(7)图【解】(1)几何不变且无多余约束。左右两边L形杆及地面分别作为三个刚片。(2)几何常变。中间三较刚架与地面构成一个刚片，其与左边倒L形刚片之间只有两根链杆相联，缺少一个约束。(3) 0、1、2、3。最后一个封闭的圆环(或框)内部有3个多余约束。(4) 4。上层可看作二元体去掉，下层多余两个较。(5) 3。下层(包括地面)几何不变，为一个刚片

26、；与上层刚片之间用三个较相联，多余3个约束。(6) 内部几何不变、0。将左上角水平杆、右上角较接三角形和下部较接三角形分别作为刚片，根据三刚片规则分析。(7) 内部几何不变、3。外围封闭的正方形框为有3个多余约束的刚片；内部较接四边形可选一对平行的对边看作两个刚片；根据三刚片规则即可分析。习题2.3对习题2.3图所示各体系进行几何组成分析。(a)(b)(c)(e)习题2.3图【解】(1)如习题解2.3(a)图所示，刚片AB与刚片I由钱A和支杆相联组成几何不变的部分；再与刚片BC由钱B和支杆相联，故原体系几何不变且无多余约束。习题解2.3(a)图(2)刚片I、II、出由不共线三校A、B、(I,出

27、)两两相联，组成几何不变的部分,如习题解2.3(b)图所示。在此部分上添加二元体C-D-E,故原体系几何不变且无多余约束。(l)(1) (j)(k)习题解2.3(b)图(3)如习题解2.3(c)图所示，将左、右两端的折形刚片看成两根链杆，则刚片I、n、m由不共线三校(I,n)、(n,出)、(1,出)两两相联，故体系几何不变且无多余约束。(I,皿)(n,皿)习题解2.3(c)图(4)如习题解2.3(d)图所示，刚片I、n、出由不共线的三校两两相联，形成大刚片；该大刚片与地基之间由4根支杆相连，有一个多余约束。故原体系为有一个多余约束的几何不变体系。(5)如习题解2.3(e)图所示，刚片I、n、出

28、组成几何不变且无多余约束的体系，为一个大刚片；该大刚片与地基之间由平行的三根杆、相联，故原体系几何瞬变。习题解2.3(e)图(6)如习题解2.3图所示，由三刚片规则可知，刚片I、n及地基组成几何不变且无多余约束的体系，设为扩大的地基。刚片ABC与扩大的地基由杆和较C相联；刚片CD与扩大的地基由杆和钱C相联。故原体系几何不变且无多余约束。习题解2.3(f)图第3章静定梁与静定刚架习题解答习题3.1是非判断题(1)在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。()(2)区段叠加法仅适用于弯矩图的绘制，不适用于剪力图的绘制。()(3)多跨静定梁在附属部分受竖向荷载作用时，必

29、会引起基本部分的内力。()(4)习题3.1(4)图所示多跨静定梁中，CDE和EF部分均为附属部分。()AbICjDEF习题3.1(4)图【解】(1)正确；(2)错误；(3)正确；(4)正确；EF为第二层次附属部分，CDE为第一层次附属部分；习题3.2填空(1)习题3.2(1)图所示受荷的多跨静定梁，其定向联系C所传递白弯矩Me的大小为截面B的弯矩大小为,侧受拉。FpFp习题3.2(1)图(2)习题3.2(2)图所示风载作用下的悬臂刚架，其梁端弯矩Mab=kNm,侧受拉；左柱B截面弯矩Mb=kNm,侧受拉。WN/Oj三三aA如m4D习题3.2(2)图(a)【解】(1)Me=0;Mc=FpI,上侧

30、受拉。CDE部分在该荷载作用下自平衡;(2) MAB=288kNm,左侧受拉；MB=32kNm,右侧受拉；习题3.3作习题3.3图所示单跨静定梁的M图和Fq图。20kN/mIA|B口CD2mI4m2ml/2(d)(c)qa5kN/m20kNmeqa210kNm(e)2m12ml2ml2m(f)习题3.3图(a)(b)*M图Fq图(c)M图M图M图（单位：kNm）Fq图（单位:kN）（f）12kNm习题3.4作习题3.4图所示单跨静定梁的内力图。4kN/m2m12ml3m2m(c)习题3.4图【解】(c)习题3.5作习题3.5图所示斜梁的内力图。5kN/mm4m2m习题3.5图【解】习题3.6作

31、习题3.6图所示多跨梁的内力图。J-EIr丈13m工3m(a)习题3.6图FQ图(单位：kN)(a)(b)(c)4m(a)4m3.8图所示刚架的内力图。【解】习题3.8图24M图(单位：kNm)DB=-L嚏12Fn图(单位:kN)Fq图(单位：kN)Fq图(单位：kN)(b)Fn图(单位:kN)第4章静定拱习题解答习题4.1是非判断题(1)三校拱的水平推力不仅与三个校的位置有关，还与拱轴线的形状有关。(2)所谓合理拱轴线，是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。(3)改变荷载值的大小，三较拱的合理拱轴线形状也将发生改变。()【解】(1)错误。从公式Fh=MC/f可知，三钱拱的水平推力

32、与拱轴线的形状无关;(2)错误。荷载发生改变时，合理拱轴线将发生变化;(3)错误。合理拱轴线与荷载大小无关；习题4.2填空(1)习题3.2(3)图所示三校拱的水平推力Fh等于习题3.2(3)图【解】(1)Fp/2；图所示三校拱支反力和指定截面K的内力。已知轴线方程习题4.3求习题3.154fy=yx(l-x)。Fha=Fhb=16kN；Fva=8kN()；Fvb=24kN()MK=-15kNm；Fqk=1.9kN；FNK=-17.8kN第5章静定平面桁架习题解答习题5.1是非判断题(1)利用结点法求解桁架结构时，可从任意结点开始。()【解】(1)错误。一般从仅包含两个未知轴力的结点开始。习题5

33、.2填空(1)习题3.2(4)图所示桁架中有根零杆。习题3.2（4）图【角单】（1）11（仅竖向杆件中有轴力，其余均为零杆）习题5.3试用结点法求习题3.10图所示桁架杆件的轴力。习题3.10图30kN30kN提示：根据零杆判别法则有:Fn13=Fn43=0；根据等力杆判别法则有:FN24=FN46后分别对结点2、3、5列力平衡方程，即可求解全部杆件的内力。提示：根据零杆判别法则有：Fn18=Fn17=Fn16=Fn27=Fn36=Fn45=0；根据等力杆判别法则有：FN12=FN23=FN34；FN78=FN76=FN65。然后取结点4、5列力平衡方程，即可求解全部杆件的内力。(b)(a)(

34、c)提示：题需先求出支座反力后，截取I.1截面以右为隔离体，由Fni2=0,然后再进行零杆判断。习题5.5用截面法求解习题3.12图所示桁架指定杆件的轴力。lbbllac111111(a)(b)31c225ba62点取矩cbaFp0；截取n.n截面，取圆圈以内为脱提示：截取I.I截面可得到提示：截取I.I截面可得到FpFNbFncFpFp12113c4891可知FNa(2)FNab、Fnc；根据零杆判断法则Fp12截取n.n截面可得到FNa3.22c=0(1)FNaFp第6章结构的位移计算习题解答习题6.1是非判断题(1)变形体虚功原理仅适用于弹性体系，不适用于非弹性体系。(2)虚功原理中的力

35、状态和位移状态都是虚设的。(3)功的互等定理仅适用于线弹性体系，不适用于非线弹性体系。()(4)反力互等定理仅适用于超静定结构，不适用于静定结构。()(5)对于静定结构，有变形就一定有内力。()(6)对于静定结构，有位移就一定有变形。()(7)习题4.1(7)图所示体系中各杆EA相同，则两图中C点的水平位移相等。()(8) Mp图，环图如习题4.1(8)图所示，EI=常数。下列图乘结果是正确的：2(-x-q-Xl)x1()EI384(9) Mp图、M图如习题4.1(9)图所示，下列图乘结果是正确的:11“(Aiy0iA2y02)A3y03EI1EI2(10)习题4.1(10)图所示结构的两个平

36、衡状态中，有一个为温度变化，此时功的互等定理不成立。()(a)(b)习题4.1(7)图IliinuInnnniillIII(a)(b)习题4.1(10)图错误。只有一个状态是虚设的。(3)正确。(4)错误。反力互等定理适用于线弹性的静定和超静定结构O(5)错误。譬如静定结构在温度变化作用下，有变形但没有内力。(6)错误。譬如静定结构在支座移动作用下，有位移但没有变形。正确。由桁架的位移计算公式可知。(8)错误。由于取yo的M图为折线图，应分段图乘。(9)正确。【解】(1)错误。变形体虚功原理适用于弹性和非弹性的所有体系。(10)正确。习题6.2填空题(1)习题4.2(1)图所示刚架，由于支座B

37、下沉所引起D点的水平位移Adh=(2)虚功原理有两种不同的应用形式，即原理和原理。其中，用于求原理。位移的是(3)用单位荷载法计算位移时，虚拟状态中所加的荷载应是与所求广义位移相应的(4)图乘法的应用条件是:且Mp与M图中至少有一个为直线图形。(5)已知刚架在荷载作用下的Mp图如习题4.2(5)图所示，曲线为二次抛物线，横梁的抗弯刚度为2EI,竖杆为EI,则横梁中点K的竖向位移为(6)习题4.2(6)图所示拱中拉杆AB比原设计长度短了1.5cm,由此引起C点的竖向位移为；引起支座A的水平反力为习题4.2(7)图所示结构，当C点有Fp=1(J)作用时,D点竖向位移等于(T),当E点有图示荷载作用

38、时，C点的竖向位移为(8)习题4.2(8)图(a)所示连续梁支座B的反力为FRBH(),则该连续梁在支座b16下沉4=1时(如图(b)所示)，D点的竖向位移O习题4.2(1)图习题4.2(6)图(a)习题4.2(5)图M=1习题4.2(7)图(b)习题4.2(8)图.A,、一二、一【斛】(1)(t)。根据公式乙Frc计算。3(1) 虚位移、虚力；虚力。(2) 广义单位力。(4) EI为常数的直线杆。48.875(5) (J)。先在K点加单位力并绘M图，然后利用图乘法公式计算。EI(6) 1.5cm;0。C点的竖向位移用公式=£Fn®计算；制造误差不会引起静定结构产生反力和内

39、力。一(7) ()。由位移互等定理可知，C点作用单位力时，E点沿M方向的位移为a621=-一。则E点作用单位力M=1时，C点产生的位移为612=-一。11(8)一(J)。对(a)、(b)两个图本状态，应用功的互等定理可得结果。16习题6.3分别用积分法和图乘法求习题4.3图所示各指定位移Acv。EI为常数。【解】1)求&V(1)积分法Fp=1,并绘M图如习题绘MP图，如习题4.3(1)(b)图所示。在C点加竖向单位力2。4.3(1)图所示。由于该两个弯矩图对称，可计算一半，再将结果乘以AC段弯矩为(2)图乘法2)求&V(1)积分法绘Mp图，如习题cv=2l/211-1cv=2-

40、日20kN/m2m(2)(c)图所示。以CMp一-x-EI22FPxdx=Fpl348EI1_22lxx3448EI“UI”川UIUUHUIWI习题4.3(2)图CEIB2m4.3(2)(b)图所示。在C点加竖向单位力并绘M图，如习题4.3点为坐标原点，x轴向左为正，求得AC段(0WxW2)弯矩为2M=x,Mp=10M(x+2)212CV=ox10(x2)2dx=6803EI(2)图乘法由计算位移的图乘法公式，得112112cv=1602-24022-1021EIIL232336803EI(八3)求&vFp=ql/2C(b)Mp图18习题4.3(3)图(1)积分法绘MP图，如习题4.3

41、(3)(b)图所示。在C点加竖向单位力并绘M图，如习题4.3(3)(c)图所示。根据图中的坐标系，两杆的弯矩(按下侧受拉求)分别为AB杆CB杆CVEI(2)图乘法cv1x,2Mp二生xqx242qlM=x,Mp=xl1ql121l/2qlql4xx-qxdxxxdx=0242EI0224EI/2_22_、11ql22l2ql21l1ql2l2lxqxlx-x_-x|x-qX-K-+-K-qX-XXEI12432382224232,ql424EI4)求中A(1)积分法绘Mp图，如习题4.3(4)(b)图所示。在A点加单位力偶并绘M图，如习题4.3(4)(c)图所示。以A为坐标原点，x轴向右为正，

42、弯矩表达式(以下侧受拉为正)为1M=1x,31312MP=-qlx-qx22cv二3iMM21EI2111x3q1xqx02EI31223q1x-1qx2dx2“2”58EIq13(2)图乘法由计算位移的图乘法公式，得鹏1-12<2112212r1)1一%=IMq1M21MM+父1+M21Mq1M1+-MJq1212EI121333J32V3；221.211靖1133383258EI,3q1x(c)M图(b)Mp图(a)习题4.4图ql2习题6.4分别用积分法和图乘法求习题4.4(a)图所示刚架C点的水平位移&h。已知EI=常数。【解】1)积分法c)图所示。各杆的弯MP、M图分别

43、如习题4.4(b)、(c)图所示，建立坐标系如(矩用x表示，分别为CD杆AB杆12M=x,MP=qlx-万qx代入公式计算，得8EIql4(>)11l112、xqlxdxx(qlxqx)dx=日20EI22)图乘法1EI2l)-x2Jql4(>)习题6.5习题4.5(a)图所示桁架各杆截面均为Ep1Md1a2d00E=2.1X108kN/m2,A=2X10与m2,v2/2C0.51A0.50.5C1(c)FN图B1一口d1d(c)FN图习题4.5图1v2d(d)FNa1电d(d)Fn图【解】绘Fnp图，如习题4.5(b)图所示。在C点加竖向单位力,并绘FN图，如习题4.5图所示。由

44、桁架的位移计算公式=£怛J,求得EA106,2CV=FPd=2.64mm(-)EA第7章力法习题解答习题7.1是非判断题(1)习题5.1(1)图所示结构，当支座A发生转动时，各杆均产生内力。+tic+t1c11+(2)(3)(4)习题5.1(1)图习题5.1(2)图习题5.1(2)图所示结构，当内外侧均升高tiC时，两杆均只产生轴力。习题5.1(3)图(a)和(b)所示两结构的内力相同。EIEI(a)习题5.1(3)图(b)习题5.1(3)图(a)和(b)所示两结构的变形相同。【解】(1)错误。BC部分是静定的附属部分，发生刚体位移，而无内力。(2)错误。刚结点会沿左上方发生线位移，进而引起所连梁柱的弯曲。(3)正确。两结构中梁两跨的抗弯刚度比值均为1:1,因此两结构内力相同。(4)错误。两结构内力相同，但图(b)结构的刚度是图(a)的一倍，所以变形只有图(a)的一半。习题7.2填空题(1)习题5.2(1)图(a)所示超静定梁的支座A发生转角&若选图(b)所示力法基本结构,则力法方程为，代表的位移条件是，其中；：1C若选图(c)所示力法基本结构时，