自控实验报告实验三-线性系统的根轨迹

1、精选优质文档-倾情为你奉上实验三 线性系统的根轨迹一、实验目的1. 熟悉MATLAB用于控制系统中的一些基本编程语句和格式。2. 利用MATLAB语句绘制系统的根轨迹。3. 掌握用根轨迹分析系统性能的图解方法。4. 掌握系统参数变化对特征根位置的影响。二、实验报告1根据内容要求，写出调试好的MATLAB语言程序，及对应的结果。2. 记录显示的根轨迹图形，根据实验结果分析根轨迹的绘制规则。3. 根据实验结果分析闭环系统的性能，观察根轨迹上一些特殊点对应的K值，确定闭环系统稳定的范围。4写出实验的心得与体会。三、实验内容请绘制下面系统的根轨迹曲线同时得出在单位阶跃负反馈下使得闭环系统稳定的K值的范

2、围。一、 1、程序代码：G=tf(1,1,8,27,38,26); rlocus (G); k,r=rlocfind(G) G_c=feedback(G,1); step(G_c)2、实验结果：专心-专注-专业selected_point = -8.8815 + 9.4658ik = 1.8560e+04r = -10.2089 + 8.3108i -10.2089 - 8.3108i 6.2089 + 8.2888i 6.2089 - 8.2888iselected_point = -9.5640 - 7.6273ik = 1.3262e+04r = -9.5400 + 7.6518i -9

3、.5400 - 7.6518i 5.5400 + 7.6258i 5.5400 - 7.6258i selected_point = -0.8436 + 1.1180ik = 3.6752r = -3.1044 + 2.0194i -3.1044 - 2.0194i -0.8956 + 1.1669i -0.8956 - 1.1669iselected_point = -0.0095 + 2.1118ik = 73.9872r = -3.9617 + 2.4724i -3.9617 - 2.4724i -0.0383 + 2.1409i -0.0383 - 2.1409i3、结果分析： 根轨迹

4、与虚轴有交点，所以在K从零到无穷变化时，系统的稳定性会发生变化。由根轨迹图和运行结果知，当0<K<73.9872时，系统总是稳定的。二、 1、程序代码：G=tf(1,12,1,23,242,1220,1000); rlocus (G); k,r=rlocfind(G) G_c=feedback(G,1); step(G_c) 2、实验结果：selected_point = -11.9076 + 2.6398ik = 1.3433e+03r = 0.4698 +10.6207i 0.4698 -10.6207i -11.9698 + 2.8634i -11.9698 - 2.8634

5、iselected_point = 0.0355 + 9.7826ik = 1.0505e+03r = -11.3838 + 2.9674i -11.3838 - 2.9674i -0.1162 + 9.9146i -0.1162 - 9.9146i3、结果分析： 根轨迹与虚轴有交点，所以在K从零到无穷变化时，系统的稳定性会发生变化。 由根轨迹图和运行结果知，当0<K<1050.5时，系统总是稳定的。三、 1、 程序代码：G=tf(0.05,1,0.,0.01914,0.1714,1,0); rlocus (G); k,r=rlocfind(G) G_c=feedback(G,1)

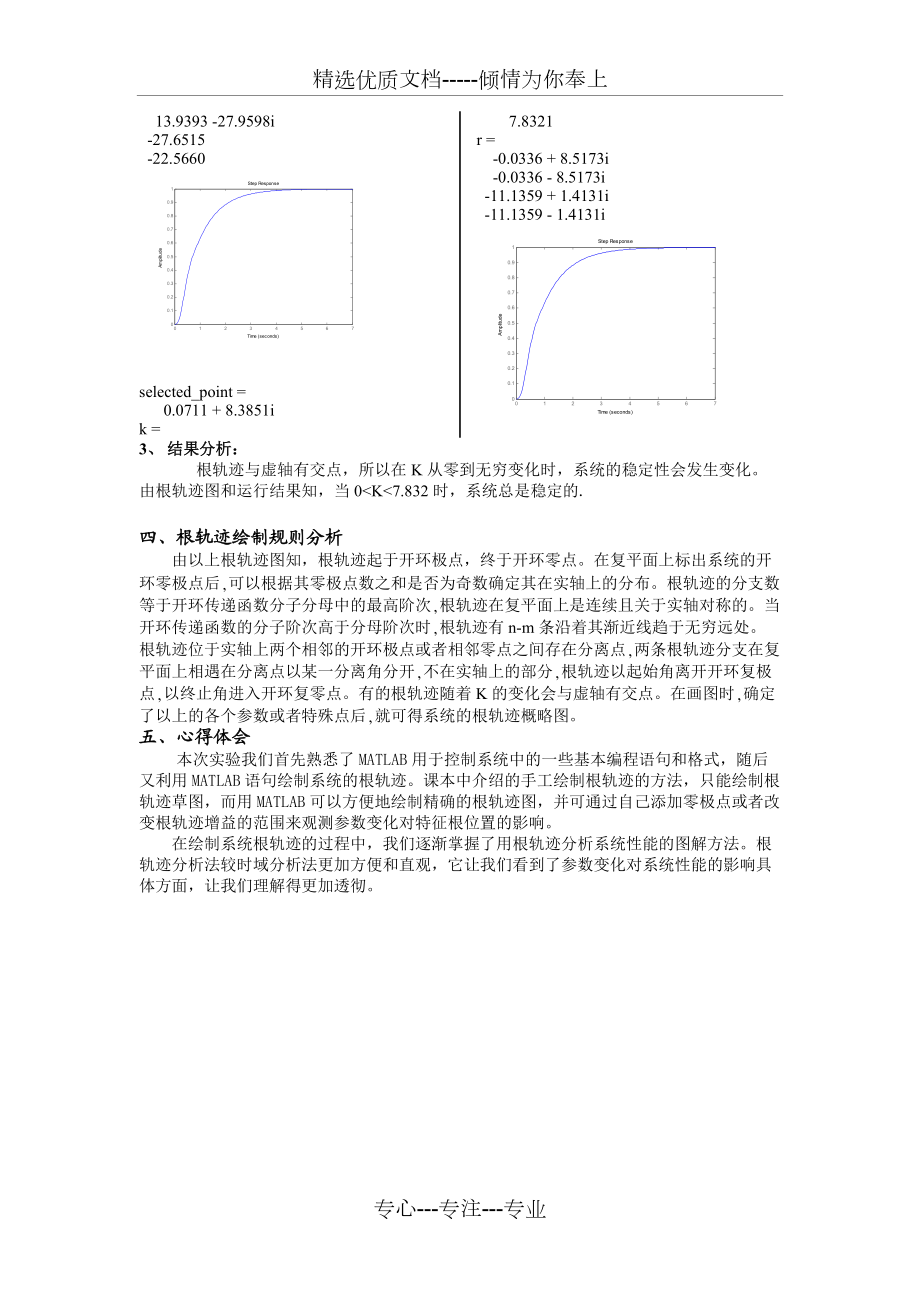
6、; step(G_c)2、实验结果：selected_point = -27.6540 + 0.1863ik = 521.8293r = 13.9393 +27.9598i 13.9393 -27.9598i -27.6515 -22.5660 selected_point = 0.0711 + 8.3851ik = 7.8321r = -0.0336 + 8.5173i -0.0336 - 8.5173i -11.1359 + 1.4131i -11.1359 - 1.4131i3、 结果分析： 根轨迹与虚轴有交点，所以在K从零到无穷变化时，系统的稳定性会发生变化。 由根轨迹图和运行结果知，

7、当0<K<7.832时，系统总是稳定的.四、根轨迹绘制规则分析 由以上根轨迹图知，根轨迹起于开环极点，终于开环零点。在复平面上标出系统的开环零极点后,可以根据其零极点数之和是否为奇数确定其在实轴上的分布。根轨迹的分支数等于开环传递函数分子分母中的最高阶次,根轨迹在复平面上是连续且关于实轴对称的。当开环传递函数的分子阶次高于分母阶次时,根轨迹有n-m条沿着其渐近线趋于无穷远处。根轨迹位于实轴上两个相邻的开环极点或者相邻零点之间存在分离点,两条根轨迹分支在复平面上相遇在分离点以某一分离角分开,不在实轴上的部分,根轨迹以起始角离开开环复极点,以终止角进入开环复零点。有的根轨迹随着K的变化会与虚轴有交点。在画图时,确定了以上的各个参数或者特殊点后,就可得系统的根轨迹概略图。五、心得体会本次实验我们首先熟悉了MATLAB用于控制系统中的一些基本编程语句和格式，随后又利用MATLAB语句绘制系统的根轨迹。课本中介绍的手工绘制根轨迹的方法，只能绘制根轨迹草图，而用MATLAB可以方便地绘制精确的根轨迹图，并可通过自己添加零极点或