第三章应变状态理论

1、整理ppt3-1 3-1 位移分量和应变分量位移分量和应变分量 两者的关系两者的关系3-2 3-2 物体内无限邻近两点位置的变化物体内无限邻近两点位置的变化 转动分量转动分量第三章第三章 应变状态理论应变状态理论3-3 3-3 转轴时应变分量的变换转轴时应变分量的变换3-4 3-4 主应变主应变 应变张量不变量应变张量不变量3-5 3-5 应变协调方程应变协调方程3-6 3-6 应力和应变的关系应力和应变的关系整理ppt 物体经过位移后，由于内部各点的位移不相同，物体经过位移后，由于内部各点的位移不相同，除刚体位移外，其大小和形状会发生改变除刚体位移外，其大小和形状会发生改变-称为称为变变形形

2、 在外力作用下物体内部各质点上的空间位置会发在外力作用下物体内部各质点上的空间位置会发生改变生改变-产生产生位移位移2、建立几何方程和应变协调方程、建立几何方程和应变协调方程1、分析一点的应变状态、分析一点的应变状态应变状应变状态理论态理论整理ppt3-13-1位移分量和应变分量位移分量和应变分量 两者的关系两者的关系OxyzPrP Ru变形前变形前变形后变形后u = R -r1, , , ,u x y zxx y zx x y z1, , , ,v x y zyx y zy x y z1, , , ,w x y zzx y zz x y z位移分量均为单值连续函数，且假定其具有三阶连续偏导数

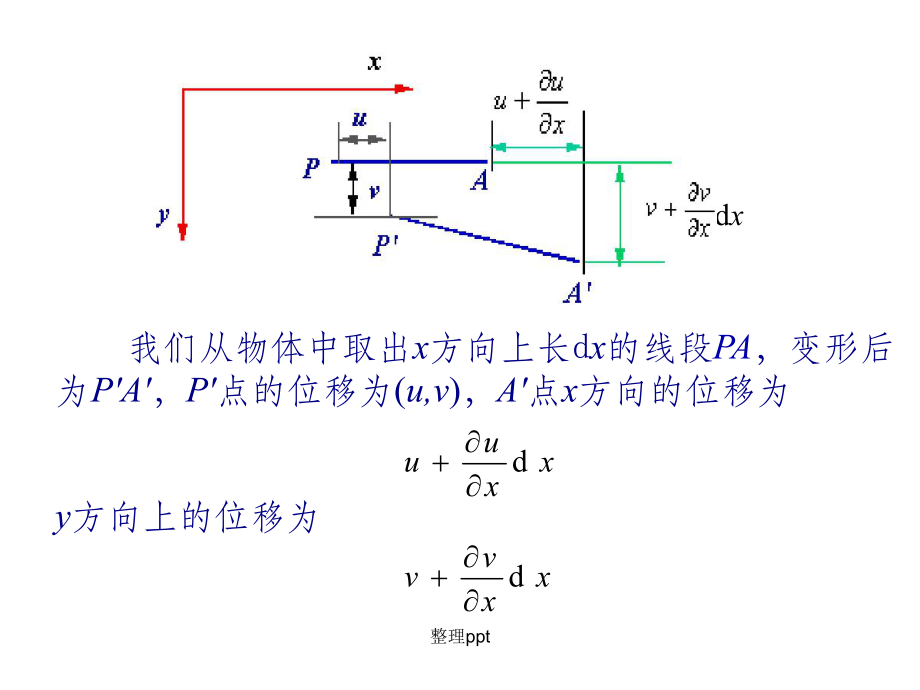
3、位移分量均为单值连续函数，且假定其具有三阶连续偏导数整理pptoyzx0l00lll轴向轴向(纵向纵向)应变应变：g g：切应变切应变g g直角改变量直角改变量,xyzxyyzzxggg六个应变分量六个应变分量整理ppt 我们从物体中取出x方向上长dx的线段PA，变形后为PA，P点的位移为(u,v)，A点x方向的位移为y方向上的位移为xxuudxxvvddxdx整理pptPA的正应变在小变形时是由x方向的位移所引起的，因此PA正应变为PA的转角为xvxuxdxdx整理ppt 我们从物体中取出y方向上长dy的线段PB，变形后为PB，B点y方向的位移为x方向上的位移为PB的正应变在小变形时是由y方

4、向的位移所引起的，因此PB正应变为yyvvdyyuudyv整理ppt线段PA的转角是线段PB的转角是于是，直角APB的改变量为yuxvxy21xvyuyuxvxygA有时用张量分量PAB整理ppt 这样，平面上一点的变形我们用该点x方向上的正应变、y方向上的正应变和xy方向构成的直角的变化切应力来描述，称为应变分量。yuxvyvxuxyyx21整理ppt 同样，空间一点同样，空间一点的变形我们用该点的变形我们用该点x x、y y、z z方向上的正应变方向上的正应变和和xy、yz、zxzx方向构方向构成的直角的变化切成的直角的变化切应变来描述。应变来描述。ijjiijxuxu21张量形式为整理p

5、pt 空间的应变分量共九空间的应变分量共九个分量，是一个对称张量，个分量，是一个对称张量，和应力张量一样，它们遵和应力张量一样，它们遵从坐标变换规则，同样存从坐标变换规则，同样存在着三个互相垂直的主方在着三个互相垂直的主方向，对应的主应变值是该向，对应的主应变值是该张量的特征值。这些互相张量的特征值。这些互相垂直的主方向构成的直角垂直的主方向构成的直角在该应变张量的变形时，在该应变张量的变形时，角度不变，由主平面组成角度不变，由主平面组成的单元体，由正方体变为的单元体，由正方体变为直角长方体。在主方向构直角长方体。在主方向构成的坐标系中，张量分量成的坐标系中，张量分量构成对角阵，切应变分量构成

6、对角阵，切应变分量为零。为零。整理ppt3-2 3-2 物体内无限邻近两点位置的变化物体内无限邻近两点位置的变化 转动分量转动分量 物体内无限邻近两点物体内无限邻近两点A和和B，坐标分别为（坐标分别为（x、y、z）和）和 （x+dx、y+dy、z+dz）, ,变形后至变形后至A和和B 点，则两点的位移点，则两点的位移矢量的三个分量为：矢量的三个分量为：A点：点：, , , ,u x y zv x y zw x y zB点：点：d ,d ,dd ,d ,dd ,d ,duu xx yy zzvv xx yy zzww xx yy zz 按按Tayior展开，得：展开，得：ddddddddduuu

7、uuxyzxyzvvvvvxyzxyzwwwwwxyzxyz 整理ppt1111ddddd22221111ddddd222212uvuuwvuuwuuxyzyzxxyzxxyzxvuvwvvuwvvvxyzxzxyyyzxyyzuwwwzx 111ddddd222wvwuwwvxyzxyyzzzxyz引引入入转转动动矢矢量量U 2xwvpyz2yuwqzx2zvurxy由由p、q、r表示单元体的刚性转角整理ppt1111ddddd22221111ddddd22221111ddddd2222xxyzxzyxyyyzzxzxyzzyxuuxyzyzvvyyzxzwwxyzxygggggg 与A点无

8、限接近的B点的位移由三部分组成：A ABB B B 随A点的一个平动绕A点的刚体转动所产生的位移由邻近的小单元体变形引起的位移整理ppt111102222dd11110dd2222dd111102222zyxxyzxzxxyyyzyxzxyzzuuxxvvyywwzzgggggg 用矩阵表示：111213212223313233112211221122xxyzxijxyyyzzxyzzgggggg-应变张量应变张量整理ppt3-3 3-3 转轴时应变分量的变换转轴时应变分量的变换 一方向为一方向为（l，m，n）的微分线段的微分线段AB，其长度为其长度为r， A点点的的坐标（坐标（x，y，z）,

9、 , B点点的坐标（的坐标（x+rl，y+rm，z+rn）uuuuurlrmrnxyzvvvvvrlrmrnxyzwwwwwrlrmrnxyz A ABB ,l mnr ,lmnr推导得：推导得：222ruvwwvuwvulmnmnlnlmxyzyzzxxy可写成：可写成：222rxyzyzzxxylmnmnlnlmggg表明：表明：如知物体内某点的如知物体内某点的6 6个应变分量，即可求得过该点的任个应变分量，即可求得过该点的任一方向微分线段一方向微分线段的相对伸长值。的相对伸长值。整理ppt 过同一点的微分线段过同一点的微分线段AB和和AC，其长度分别为其长度分别为r1和和r2 ， 方方向

10、分别为向分别为( (l1 ,m1 , n1) )和和( (l2 ,m2 , n2) )，研究变形后其夹角的改变，研究变形后其夹角的改变可推导得出转轴时应变分量的变换公式可推导得出转轴时应变分量的变换公式可写成：可写成：i jiji ij jn n 12miji ij js ng整理ppt662350030002212300400100103333010020013644 10r 例题3-1 在物体内的一点的应变张量为：65003000300400100100100200ij的微分面上的正应变。221,333lmn试求法线方向余弦为：整理ppt3-4 3-4 主应变主应变 应变张量不变量应变张量

11、不变量 物体内存在物体内存在3 3个互相垂直的方向，在这个互相垂直的方向，在这3 3个方向的微分线段个方向的微分线段，在物体变形后仍保持垂直。此方向称为在物体变形后仍保持垂直。此方向称为应变主方向应变主方向，该方向上，该方向上微分线段的相对伸长，称为微分线段的相对伸长，称为主应变主应变。 由于主方向的线段在变形后仍保持垂直，故在变形中，由于主方向的线段在变形后仍保持垂直，故在变形中，其单元体只有刚体转动，据此，可得主应变和主应变方向所其单元体只有刚体转动，据此，可得主应变和主应变方向所应满足的方程：应满足的方程：110221102211022xxyxzyxyyzzxzyzlmnlmnlmngg

12、gggg有非零解有非零解1122110221122xxyxzyxyyzzxzyzgggggg整理ppt321230JJJ其中：其中：1xyzJ222214xyyzzxxyyzzxJ ggg3112211221122xxyxzyxyyzzxzyzJgggggg-应变张量的第一不变量应变张量的第一不变量（体积应变）（体积应变）-应变张量的第二不变量应变张量的第二不变量-应变张量的第三不变量应变张量的第三不变量可得可得3 个实根，分别代表三个个实根，分别代表三个主应变，用主应变，用1、2、3表示表示整理ppt主应变的几个重要性质：主应变的几个重要性质：1、如、如123，即方程无重根，则应变主方向必相

13、互垂直。，即方程无重根，则应变主方向必相互垂直。2、如、如1=23，方程有两重根，则，方程有两重根，则3方向必同时垂直于方向必同时垂直于1、2 的方向，而的方向，而1和和2的方向可以垂直，也可以不垂直；即的方向可以垂直，也可以不垂直；即与与3垂直的任何方向都是主方向。垂直的任何方向都是主方向。3、如、如1=2=3，方程有三重根，则，方程有三重根，则3个个方向可以垂直，也方向可以垂直，也可以不垂直；即任何方向都是主方向。可以不垂直；即任何方向都是主方向。整理ppt例题3-2 在物体内的一点的应变张量为：15000040600600ij 试求主应变和主方向。解：1、三个应变张量不变量： 12222

14、2223150400110141150404000 150012009600411221500011040605400002206001122xyzxyyzzxxyyzzxxxyxzyxyyzzxzyzJJJ ggggggggg 2、由特征方程得：321230JJJ123150,43.3,83.3 整理ppt123150,43.3,83.3 2、分别代入下列方程中得：及2220lmn1112223331,0,00,0.585,0.8110,0.811,0.585lmnlmnlmn 110221102211022xxyxzyxyyzzxzyzlmnlmnlmngggggg整理ppt3-5 3-5

15、 应变协调方程应变协调方程将二、三式分别对z,y求二阶导数再相加，得zwyvxuzyxyuxvxwzuzvywxyzxyz212121类似可以得到另外两个方程整理ppt将右边后三式分别对将右边后三式分别对x, ,y, ,z求导求导后两式相加减去第一式，后两式相加减去第一式，再对再对x求导，得求导，得zwyvxuzyxyuxvxwzuzvywxyzxyz212121类似可以得到类似可以得到另外两个方程另外两个方程整理ppt综合得：综合得：-应变协调方程应变协调方程（圣维南方程）（圣维南方程）整理ppt3-6 3-6 应力和应变的关系应力和应变的关系kkijijijEE1张量形式为 应力应变的物理关系应力应变的物理关系 在线弹性力学中，应力在线弹性力学中，应力应变的物理关系成线性应变的物理关系成线性的广义胡克关系，对于的广义胡克关系，对于各向同性材料，其中，各向同性材料，其中，只有两个弹性常数只有两个弹性常数. .整理ppt 当坐标系为主方向时，切应力为零，切应变也为零，公式简化为213313223211111EEE123 1 2E上三式相加可得到：其中分别为体积应变和体积应力