中考一轮复习专题二次函数的应用(实际问题)

1、学习好资料欢迎下载2012年全国中考数学试题分类解析汇编二次函数的应用（实际问题）、选择题221. （2012四川资阳3分）如图是二次函数 y=ax +bx+c的部分图象，由图象可知不等式ax +bx+c<0的解集是A. 1<x<5B. x>5C.二、填空题1. （2012浙江绍兴5分）教练对小明推铅球的录像进行技术分析，发现铅球行进高度y （m）与水平距离 x（m）之间的关系为y =1 ,、2 c ,一（x -4）2 +3 ,由此可知铅球推出的距离是12m。*y=ax2+bx .小强的高度相同，则小强骑自行车通过拱梁部分的桥面OC共需 秒.、解答题1. （2012重庆

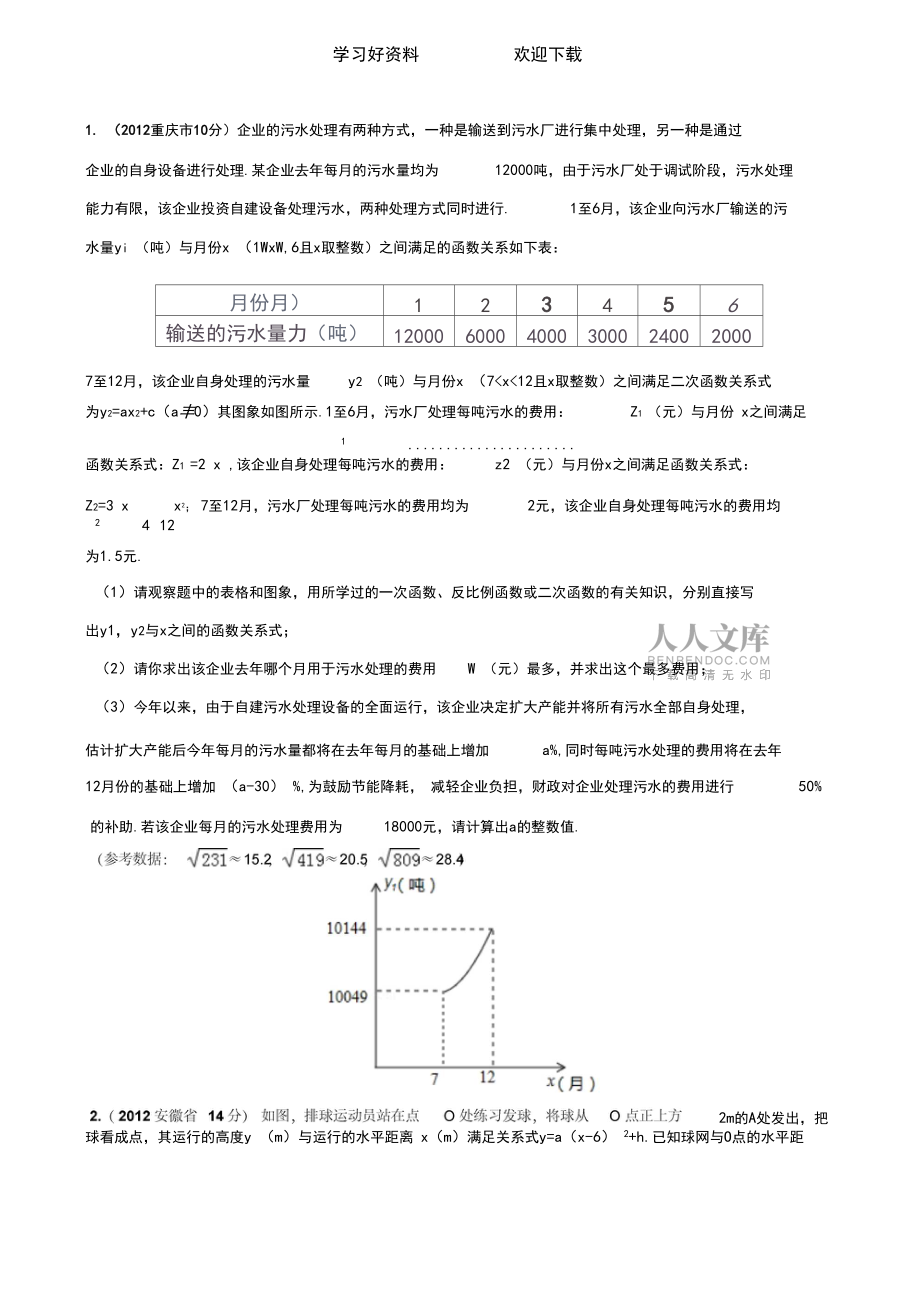
2、市10分）企业的污水处理有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行.1至6月，该企业向污水厂输送的污水量yi （吨）与月份x （1WxW,6且x取整数）之间满足的函数关系如下表：月份月）123456输送的污水量力（吨）12000600040003000240020007至12月，该企业自身处理的污水量y2 （吨）与月份x （7<x<12且x取整数）之间满足二次函数关系式为y2=ax2+c（a丰0）其图象如图所示.1至

3、6月，污水厂处理每吨污水的费用：Z1 （元）与月份 x之间满足1 函数关系式：Z1 =2 x ,该企业自身处理每吨污水的费用：z2 （元）与月份x之间满足函数关系式：Z2=3 xx2； 7至12月，污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均2 412为1.5元.（1）请观察题中的表格和图象，用所学过的一次函数、反比例函数或二次函数的有关知识，分别直接写出y1，y2与x之间的函数关系式；（2）请你求出该企业去年哪个月用于污水处理的费用W （元）最多，并求出这个最多费用；（3）今年以来，由于自建污水处理设备的全面运行，该企业决定扩大产能并将所有污水全部自身处理，估计扩大产能后

4、今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加 （a-30） %,为鼓励节能降耗， 减轻企业负担，财政对企业处理污水的费用进行50%的补助.若该企业每月的污水处理费用为18000元，请计算出a的整数值.2m的A处发出，把球看成点，其运行的高度y （m）与运行的水平距离 x（m）满足关系式y=a（x-6） 2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距 。点的水平距离为18m。（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；（3）若球一

5、定能越过球网，又不出边界，求h的取值范围。3. （2012浙江嘉兴、舟山12分）某汽车租赁公司拥有 20辆汽车.据统计，当每辆车的日租金为 400元时，可全部租出；当每辆车的日租金每增加50元，未租出的车将增加 1辆；公司平均每日的各项支出共4800元.设公司每日租出工辆车时，日收益为y元.（日收益=日租金收入一平均每日各项支出）（1）公司每日租出x辆车时，每辆车的日租金为元（用含 x的代数式表示）；（2）当每日租出多少辆时，租赁公司日收益最大？最大是多少元？（3）当每日租出多少辆时，租赁公司的日收益不盈也不亏？4. （2012浙江台州12分）某汽车在刹车后行驶的距离s （单位：米）与时间t

6、（单位：秒）之间的关系得部分数据如下表：时间t （秒）00.20.40.60.81.01.2行驶距离s （米）02.85.27.28.81010.8（1）根据这些数据在给出的坐标系中画出相应的点；（2）选择适当的函数表示 s与t之间的关系，求出相应的函数解析式;（3）刹车后汽车行驶了多长距离才停止？当t分别为3 t2 （t1t2）时，对应s的值分别为S1, S2,请比较s1与攵的大小，并解释比较结果的实 t1 t2际意义.5. (2012江苏常州7分)某商场购进一批 L型服装(数量足够多)，进价为40元/件，以60元/件销售，每天销售20件。根据市场调研，若每件每降1元，则每天销售数量比原来多

7、3件。现商场决定对 L型服装开展降价促销活动，每件降价 x元(x为正整数)。在促销期间，商场要想每天获得最大销售利润，每件降价多少元？每天最大销售毛利润为多少？(注：每件服装销售毛利润指每件服装的销售价与进货价的差)6. (2012江苏无锡8分)如图，在边长为24cm的正方形纸片 ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒( A. B. C. D四个顶点正好重合于上底面上一点).已知E、F在AB边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x(cm).(1)若折成的包装盒恰好是个正方体，试求这个包装盒的体积V;(2)

8、某广告商要求包装盒的表面(不含下底面)面积S最大，试问x应取何值？QCA E尸 37. (2012江苏盐城12分)知识迁移:当a >0且x >0时，因为>0,所以x-2Va a-却从而x + a或遍(当 xxx = J时取等号).记函数y =x+a(a >0,x >0),由上述结论可知：当x = J-时，该函数有最小值为 2J-. x1 直接应用：已知函数y1=x(xA0)与函数y2= (xA0),则当x =时，y1 + y2取得最小值 x为.变形应用：已知函数y1 =x+1(x > 1)与函数y2 =(x+1)2+4(xa -1)，求X的最小值，并指出取得

9、该 y1，共360元；二是燃油费，每最小值时相应的x的值.实际应用：已知某汽车的一次运输成本包含以下三个部分：一是固定费用千米为1.6元；三是折旧费，它与路程的平方成正比，比例系数为0.001.设该汽车一次运输的路程为x千米，求当x为多少时，该汽车平均每千米的运输成本最低？最低是多少元？8. (2012江苏扬州12分)已知抛物线y=ax2+bx+c经过A( 1 , 0)、B(3 , 0)、C(0, 3)三点，直线l是抛 物线的对称轴.(1)求抛物线的函数关系式；(2)设点P是直线l上的一个动点，当 PAC的周长最小时，求点 P的坐标；(3)在直线l上是否存在点 M,使 MAC为等腰三角形？若存

10、在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由.9. (2012福建莆田8分)如图，某种新型导弹从地面发射点L处发射，在初始竖直加速飞行阶段，导弹上12 1升的图度y(km)与飞行时间x(s)之间的关系式为y = x2+ x (0 E x E 10) .发射3 s后，导弹到达A点,186此时位于与L同一水平面的R处雷达立测得 AR的距离是2 km,再过3s后，导弹到达B点.(4分)求发射点L与雷达站R之间的距离；(2)(4分)当导弹到达B点时，求雷达站测得的仰角 (即/ BRL)的正切值.!sA距n 7LR10. (2012湖北武汉10分)如图，小河上有一拱桥，拱桥及河道的截面轮廓

11、线由抛物线的一部分ACB和矩形的三边 AE, ED, DB组成，已知河底 ED是水平的，ED=16m, AE=8m,抛物线的顶点 C至U ED的 距离是11m,以ED所在的直线为x轴，抛物线的对称轴为 y轴建立平面直角坐标系.（1）求抛物线.的解析式；（2）已知从某时刻开始的 40h内，水面与河底 ED的距离h（单位：m）随时间t（单位：h）的变化满足函数、，一 .12关系h= 128（t 19） +8（0 -t -40）且当水面到顶点 C的距离不大于5m时，需禁止船只通行，请通过计算11. （2012湖北黄冈12分）某科技开发公司研制出一种新型产品，每件产品的成本为2400元，销售单价定为3

12、000元.在该产品的试销期间，为了促销，鼓励商家购买该新型产品，公司决定商家一次购买这种 新型产品不超过10件时，每件按3000元销售；若一次购买该种产品超过10件时，每多购买一件，所购买的全部产品的销售单价均降低10元，但销售单价均不低于 2600元.（1）商家一次购买这种产品多少彳时，销售单价恰好为2600元？（2）设商家一次购买这种产品 x件，开发公司所获的利润为 y元，求y（元）与x（件）之间的函数关系式，并 写出自变量x的取值范围.（3）该公司的销售人员发现：当商家一次购买产品的件数超过某一数量时，会出现随着一次购买的数量 的增多，公司所获的利润反而减少这一情况.为使商家一次购买的数

13、量越多，公司所获的利润越大，公司应 将最低销售单价调整为多少元 ？（其它销售条件不变）12. （2012湖南岳阳10分）我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物 线组合而成的封闭图形，不妨简称为锅线”，锅口直径为6dm,锅深3dm,锅盖高1dm （锅口直径与锅盖直径视为相同），建立直接坐标系如图所示，如果把锅纵断面的抛物线的记为Ci ,把锅盖纵断面的抛物线记为c2.（1）求Ci和C2的解析式；（2）如图，过点 B作直线BE: y= 1x - 1交C1于点E （ - 2,-刍），连接OE、BC ,在x轴上求一点33P,使以点P、B、C为顶点的 PBC与BOE相似，求出

14、 P点的坐标；（3）如果（2）中的直线BE保持不变，抛物线 Ci或C2上是否存在一点 Q,使得 EBQ的面积最大？若 存在，求出Q的坐标和 EBQ面积的最大值；若不存在，请说明理由.13. (2012四川达州若矩形的周长为的函数关系式为:提出新问题图8分)问题背景1,则可求出该矩形面积的最大值我们 可以设矩形的一边长为X,面积为s,则s与21S = B2 + x(x > 0 ),利用函数的图象或通过配方均可求得该函数的最大值 2若矩形的面积为1,则该矩形的周长有无最大值或最小值？若有，最大(小)值是多少?分析问题1若设该矩形的一边长为x,周长为y,则y与x的函数关系式为：y =2(x +

15、-)(x > 0 ),问题就转化为x研究该函数的最大(小)值了解决问题借鉴我们已有的研究函数的经验，探索函数1，一 ，y=2(x+)(x>0 )的最大(小)值. x(1)实践操作：填写下表，并用描点法画出函数1一y =2（x 十一）（x > 0 ）的图象: x12341（2）观察猜想：观察该函数的图象，猜想当 x=时，函数y =2（x+）（x> 0）有最值（填大”或小”），是.1（3）推理论 证：问题背景中提到，通过配万可求二次函数s = -x2+x（x > 0 ）的最大值，请你尝试通过配方求函数y_2（x+1）（x>0师最大（小）值，以证明你的猜想.提示：

16、当x>0时， x = （6）214. （2012四川巴中9分）某商品的进彳为每件 50元，售价为每件60元，每个月可卖出 200件。如果每 件商品的售价上涨1元，则每个月少卖10件（每件售价不能高于 72元）。设每件商品的售价上涨 x元（x 为整数），每个月的销售利润为 y元，（1）求y与x的函数关系式，并直接写出 x的取值范围；（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大月利润是多少元？15. （2012辽宁锦州10分）某商店经营儿童益智玩具，已知成批购进时的单价是20元.调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨 1元，月销售量就减少10件，但

17、每件玩具售价不能 高于40元.设每件玩具的销售单价上涨 了 x元时（x为正整数），月销售利润为y元.（1）求y与x的函数关系式并直接写出自变量x的取值范围.（2）每件玩具的售价.定为多少元时，月销售利润恰为2520元？（3）每件玩具的售价.定为多少元时可使月销售利润最大？最大的月利润是多少？16. （2012河北省9分）某工厂生产一种合金薄板（其厚度忽略不计），这些薄板的形状均为正方形，边长（单位：cm）在550之间.每张薄板的成本价（单位：元）与它的面积（单位：cm2）成正比例，每张薄板的出厂价（单位：元）由基础价和浮动价两部分组成，其中基础价与薄板的大小无关，是固定不变的.浮动价与薄板的边

18、长成正比例.在营销过程中得到了表格中的数据.薄板的边长（cm）2030出厂价（元/张）5070（1）求一张薄板的出厂价与边长之间满足的函数关系式；（2）已知出厂一张边长为 40cm的薄板，获得的利润为 26元（利润=出厂价-成本价），求一张薄板的利润与边长之间满足的函数关系式.当边长为多少时，出厂一张薄板所获得的利润最大？最大利润是多少？ c 1 b 4ac-b2参考公式：抛物线： y=ax2+ bx+ c （aw。的顶点坐标为 一一， -12a 4a ,17. （2012黑龙江大庆6分）将一根长为16兀厘米的细铁丝剪成两段.并把每段铁丝围成圆，设所得两圆 半径分别为q和r2.（1）求1与r2的关系式，并写出1的取值范围；（2）将两圆的面积和 S表示成1的函数关系式，求 S的最小值.18. （2012黑龙江哈尔滨6分）小磊要制作一个三角形的钢架模型，在这个三角形中，长度为 x（单位：cm） 的边与这条边上的高之和为40 cm,这个三角形的面积 S（单位：cm2）随x（单位：cm）的变化而变化.（