线性系统的频域分析自动控制

1、实验三·线性系统的频域分析一、 实验目的1掌握用MATLAB语句绘制各种频域曲线。2掌握控制系统的频域分析方法。二、 实验内容 1.典型二阶系统绘制出，0.3，0.5，0.8，2的bode图，记录并分析对系统bode图的影响。 2.系统的开环传递函数为绘制系统的Nyquist曲线、Bode图和Nichols图，说明系统的稳定性，并通过绘制阶跃响应曲线验证。 3.已知系统的开环传递函数为。求系统的开环截止频率穿越频率、幅值裕度和相位裕度。应用频率稳定判据判定系统的稳定性。三、 实验内容及分析1. 系统1：中，（1）时 Matlab文本如下：num=36 0 0;den=1 1.2 36

2、;w=logspace(-2,3,100);bode(num,den,w)Grid得到图像：同理，得到其他值情况下的波特图：=0.3时=0.5时=0.8时=2时从上面的图像中可以看出：随着的不断增大，波特图中震荡的部分变得越来越平滑。而且，对幅频特性曲线来说，其上升的斜率越来越慢；对相频特性曲线来说，下降的幅度也在变缓。2. 开环传递函数1：奈奎斯特图函数及图像如下：num=0 10;den=conv(5,-1,1,5),0,0;z,p,k=tf2zp(num,den); pnyquist(num,den)结果：p =0 0 -5.0000 0.2000从上面的结果可知：在右半平面根的个数P=

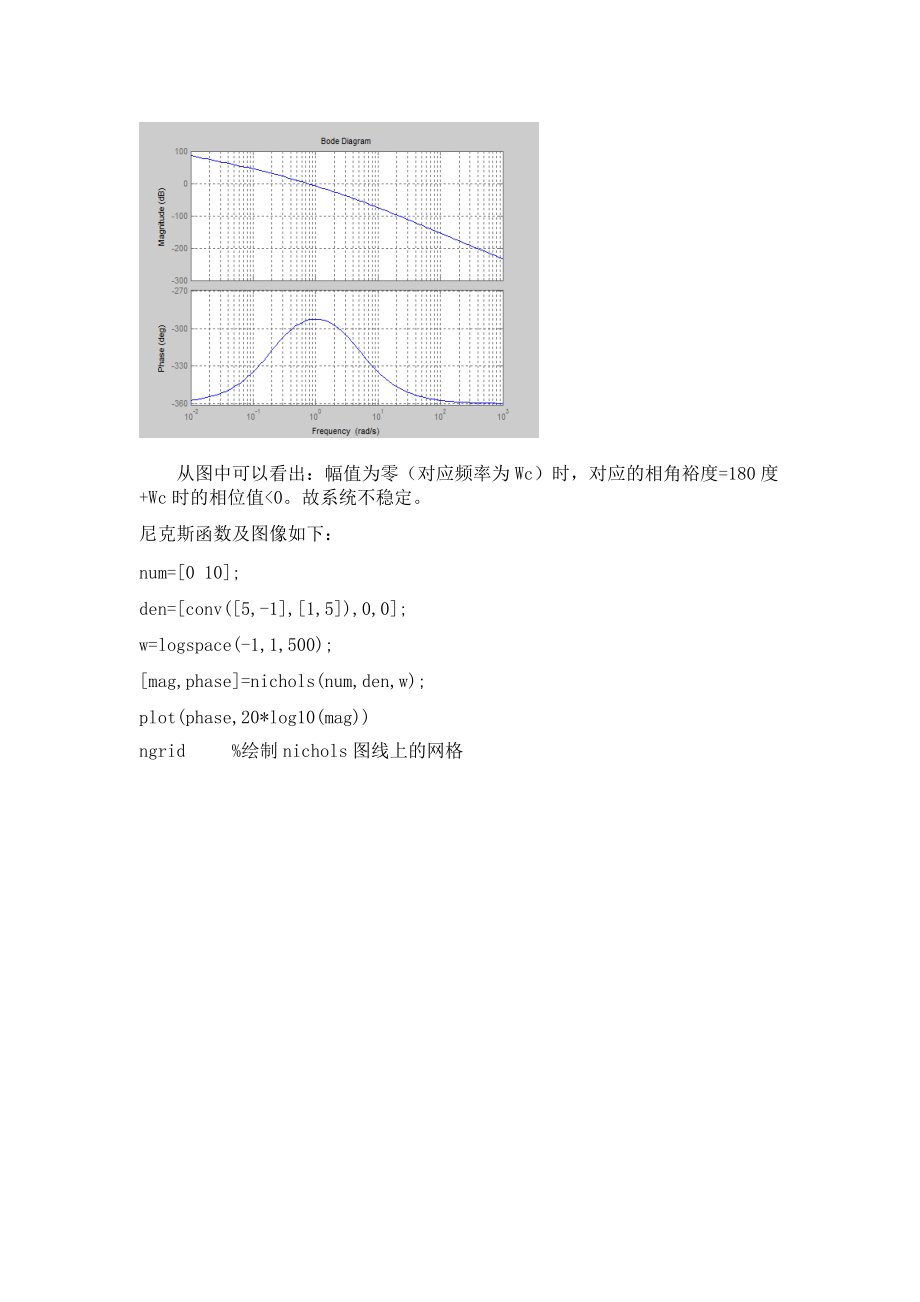
3、1。系统的Nyquist图不包围（-1，j0）点，R=0不等于P=1，闭环系统不稳定。波特图函数及图像如下：num=0 10;den=conv(5,-1,1,5),0,0;w=logspace(-2,3,100);bode(num,den,w)grid 从图中可以看出：幅值为零（对应频率为Wc）时，对应的相角裕度=180度+Wc时的相位值<0。故系统不稳定。尼克斯函数及图像如下：num=0 10;den=conv(5,-1,1,5),0,0;w=logspace(-1,1,500);mag,phase=nichols(num,den,w);plot(phase,20*log10(mag)

4、ngrid %绘制nichols图线上的网格阶跃响应函数及图像如上右图：num=0 10;den=conv(5,-1,1,5),0,0; step(num,den) %调用阶跃响应函数求取单位阶跃响应曲线 grid %画网格标度线 xlabel('t/s'),ylabel('c(t)') %给坐标轴加上说明title('Unit-step Respinse of G(s)=25/(s2+4s+25)') %给图形加上标题名分析：曲线先平稳然后急剧上升，故闭环不稳定，验证了Nyquist图判断结论的正确性。开环传递函数2：奈奎斯特函数及图像如下：n

5、um=8 8;den=conv(1,15,1,6,10),0,0;z,p,k=tf2zp(num,den); pnyquist(num,den)p = 0 0 -15.0000 -3.0000 + 1.0000i -3.0000 - 1.0000i从上面的结果可知：在右半平面根的个数P=0。系统的Nyquist图不过（-1，j0）点，R=0等于P=0，闭环系统不稳定。波特函数及图像如下：num=8 8;den=conv(1,15,1,6,10),0,0;w=logspace(-2,3,100);bode(num,den,w)grid尼克斯函数及图像如上右图：num=8 8;den=conv(1

6、,15,1,6,10),0,0;w=logspace(-1,1,500);mag,phase=nichols(num,den,w);plot(phase,20*log10(mag)ngrid %绘制nichols图线上的网格阶跃响应函数及图像如下：num=8 8;den=conv(1,15,1,6,10),0,0; step(num,den) %调用阶跃响应函数求取单位阶跃响应曲线 grid %画网格标度线 xlabel('t/s'),ylabel('c(t)') %给坐标轴加上说明 title('Unit-step Respinse of G(s)=2

7、5/(s2+4s+25)')%给图形加上标题名开环传递函数3：奈奎斯特函数及图像如下：num=4/3 4;den=conv(0.02,1,conv(1,15,1,6,10),0;z,p,k=tf2zp(num,den); pnyquist(num,den)p = 0 -50.0000 -15.0000 -3.0000 + 1.0000i -3.0000 - 1.0000i从上面求得的根可知该系统稳定波特函数及图像如下：num=4/3 4;den=conv(0.02,1,conv(1,15,1,6,10),0;w=logspace(-2,3,100);bode(num,den,w)gri

8、d尼克斯函数及图像如下：num=4/3 4;den=conv(0.02,1,conv(1,15,1,6,10),0;w=logspace(-1,1,500);mag,phase=nichols(num,den,w);plot(phase,20*log10(mag)ngrid %绘制nichols图线上的网格阶跃响应函数及图像：num=4/3 4;den=conv(0.02,1,conv(1,15,1,6,10),0; step(num,den) %调用阶跃响应函数求取单位阶跃响应曲线 grid %画网格标度线 xlabel('t/s'),ylabel('c(t)'

9、;) %给坐标轴加上说明 title('Unit-step Respinse of G(s)=25/(s2+4s+25)') %给图形加上标题名开环传递函数其在matlab中取得的开环截止频率、穿越频率、幅值裕度和相位裕度分别为：num=1 1; den=0.1 1 0 0;gm,pm,wcg,wcp=margin(num,den);gm,pm,wcg,wcp 结果：gm = 0pm = 44.4594wcg = 0wcp =1.2647分析：在截至频率时，相角裕度大于零，故系统稳定。四、 实验结果与心得本次试验主要有三大内容：1. 对二阶系统中参数进行分析，实验表明：当阻尼比增大时，阻尼振荡频率Wd会减小，当>=1时，W