



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1、精选优质文档-倾情为你奉上平行线与相交线单元检测【巩固基础训练】题型发散 1.选择题,把正确答案的代号填入题中括号内(1)下列命题中,正确的是 ( )(A)有公共顶点,且方向相反的两个角是对顶角(B)有公共点,且又相等的角是对顶角(C)两条直线相交所成的角是对顶角(D)角的两边互为反向延长线的两个角是对顶角(2)下列命题中,是假命题的为 ( )(A)邻补角的平分线互相垂直(B)平行于同一直线的两条直线互相平行(C)垂直于同一直线的两条直线互相垂直(D)平行线的一组内错角的平分线互相平行(3)如果一个角的两边分别平行于另一个角的两边,那么这两个角 ( ) (A)相等 (B)互补(C)相等或互补
2、(D)以上结论都不对(4)已知下列命题内错角相等;相等的角是对顶角;互补的两个角是一定是一个为锐角,另一个为钝角;同旁内角互补其中正确命题的个数为 ( )(A)0 (B)1 (C)2 (D)3(5)两条直线被第三条直线所截,则 ( )(A)同位角的邻补角一定相等(B)内错角的对顶角一定相等(C)同位角一定不相等(D)两对同旁内角的和等于一个周角(6)下列4个命题相等的角是对顶角;同位角相等;如果一个角的两边分别平行于另一个角的两边,则两个角一定相等;两点之间的线段就是这两点间的距离其中正确的命题有 ( )(A)0个 (B)1个 (C)2个 (D)3个(7)下列条件能得二线互相垂直的个数有 (
3、)一条直线与平行线中的一条直线垂直;邻补角的两条平分线;平行线的同旁内角的平分线;同时垂直于第三条直线的两条直线(A)4个 (B)3个 (C)2个 (D)1个(8)因为AB/CD,CD/EF,所以AB/EF,这个推理的根据是 ( )(A)平行线的定义(B)同时平行于第三条直线的两条直线互相平行(C)等量代换(D)同位角相等,两直线平行(9)如图2-55如果AFE+FED=,那么 ( )(A)AC/DE (B)AB/FE(C)EDAB (D)EFAC(10)下列条件中,位置关系互相垂直的是 ( )对顶角的平分线;邻补角的平分线;平行线的同位角的平分线;平行线的内错角的平分线;平行线的同旁内角的平
4、分线(A) (B) (C) (D)2.填空题(1)把命题“在同一平面内没有公共点的两条直线平行”写成“如果,那么”形式为_(2)直线外一点与直线上各点连结的所有线段中,_最短(3)两条平行线被第三条直线所截,同旁内角的比为2:7,则这两个角的度数为_.(4)如果A为B的邻补角,那么A的平分线与B的平分线必_.(5)如图2-56AB/CD(已知),ABC=_( )_=_(两直线平行,内错角相等),BCD+_=( )3=4(已知),_( )FAD=FBC(已知),_( )(6)如图2-57,直线AB,CD,EF被直线GH所截,1=,2=,3=求证:AB/CD证明:1=,3=(已知),1=3( )
5、_( )2=,3=( ),_+_=_,_/_,AB/CD( )(7)如图2-58,直线DE,AC被第三条直线BA所截,则1和2是_,如果1=2,则_/_,其理由是( ) 3和4是直线_、_,被直线_所截,因此_/_3_4,其理由是( )(8)如图2-59,已知AB/CD,BE平分ABC,CE平分BCD,求证1+2=证明: BE平分ABC(已知),2=_( )同理1=_,1+2=_( )又AB/CD(已知),ABC+BCD=_( )1+2=( )(9)如图2-60,E、F、G分别是AB、AC、BC上一点如果B=FGC,则_/_,其理由是( )BEG=EGF,则_/_,其理由是( )如果AEG+E
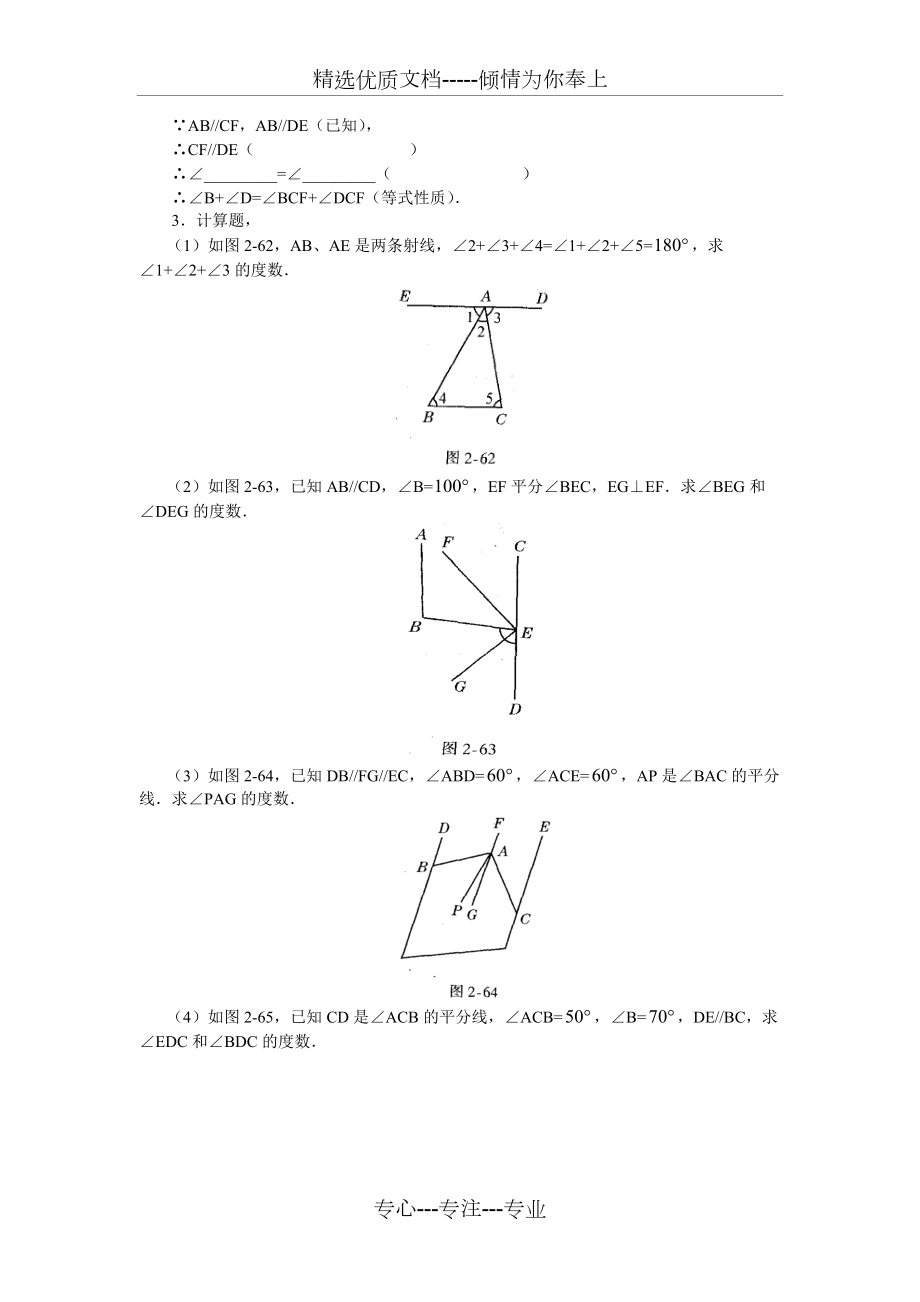
6、AF=,则_/_,其理由是( )(10)如图2-61,已知AB/CD,AB/DE,求证:B+D=BCF+DCF证明: AB/CF(已知),_=_(两直线平行,内错角相等)AB/CF,AB/DE(已知),CF/DE( )_=_( )B+D=BCF+DCF(等式性质)3计算题,(1)如图2-62,AB、AE是两条射线,2+3+4=1+2+5=,求1+2+3的度数(2)如图2-63,已知AB/CD,B=,EF平分BEC,EGEF求BEG和DEG的度数(3)如图2-64,已知DB/FG/EC,ABD=,ACE=,AP是BAC的平分线求PAG的度数(4)如图2-65,已知CD是ACB的平分线,ACB=,
7、B=,DE/BC,求EDC和BDC的度数纵横发散1如图2-66,已知C=D,DB/ECAC与DF平行吗?试说明你的理由2如图2-67,已知1=2,求3+4的度数解法发散 1如图2-68,已知AB/CD,EFAB,MNCD求证:EF/MN(用两种方法说明理由)2如图2-69,、,是直线,1= a与b平行吗?简述你的理由(用三种方法,简述你的理由)变更命题发散如图2-70,AB/CD,BAE=,ECD=,EF平分AEC,求AEF的度数如图2-71,已知AB/CD,BAE=,DCE=,EF、EG三等分AEC(1)求AEF的度数;(2)EF/AB吗?为什么?3如图2-72,已知1=,2=80°
8、;,3=,那么4是多少度?4如图2-73,AB、CD、EF、MN构成的角中,已知1=2=3,问图中有平行线吗?如果有,把彼此平行的直线找出来,并说明其中平行的理由5如图2-74,已知1+2=,3=求4的度数?6如图2-75,已知/m,求x,y的度数7如图2-76,直线分别和直线相交,1与3互余,2与3的余角互补,4=求3的度数转化发散 1如图2-77,已知AEF=B,FEC=GHB,GH垂直于AB,G为垂足,试问CE,能否垂直AB,为什么?2如图2-78,已知ADE=B,FGAB,EDC=GFB,试问CD与AB垂直吗?简述你的理由分解发散 发散题 如图2-79,AB/CD, 1=2,3=4,求
9、EMF的度数综合发散1证明:两条平行线被三条直线所截的一对同旁内角的角平分线互相垂直2求证:两条直线被第三条直线所截,若一组内错角的角平分线互相平行,则这两条直线也相互平行3在ABC中,CD平分ACB,DE/AC交BC于E,EF/CD交AB于F,求证:EF平分DEB4线段AB被分成2:3:4三部分,已知第一和第三两倍分的中点间的距离是5.4cm,求AB的长5已知:如图2-80,AB/CD,ADDB,求证1与A互余【提高能力测试】题型发散选择题,把正确答案的代号填入括号内(1)如图2-81,能与构成同旁内角的角有( )(A)1个 (B)2个(C)5个 (D)4个(2)如果两个角的两条边分别平行,
10、而其中一个角比另一个角的4倍少30°,那么这两个角是( )(A) (B)都是(C)或, (D)以上答案都不对(3)如图2-82,AB/CD,MP/AB,MN平分 AMDA=40°,D=30°,则NMP等于( )(A) (B) (C) (D)(4)如图2-83,已知:1=2,3=4,求证:AC/DF,BC/EF证明: 1=2(已知),(A)AC/DF(同位角相等,两直线平行)3=5(内错角相等,两直线平行)(B)3=4(已知)(C)5=4(等量代换)(D)BC/EF(内错角相等,两直线平行)则理由填错的是( )(5)如图2-84,已知AB/CD,HL/FG,EFCD
11、,1=,那么,EHL的度数为( )(A) (B)(C) (D)(6)直线,D、A是上的任意两点,且A在D的右侧,E、B是上任意两点,且B在E的右侧,C是和之间的某一点,连结CA和CB,则( )(A)ACB=DAC+CBE(B)DAC+ACB+CBE=(C)(A)和(B)的结论都不可能(D)(A)和(B)的结论有都可能(7)如图2-85,如果1=2,那么( )(A)AB/CD(内错角相等,两直线平行)(B)AD/BC(内错角相等,两直线平行)(C)AB/CD(两直线平行,内错角相等)(D)AD/BC(两直线平行,内错角相等)(8)如图2-86,AB/EF,设C=,那么x、y和z的关系是( )(A
12、)(B)(C)(D)(9)如图2-87,1:2:3=2:3:4,EF/BC,DF/EB,则A:B:C=( )(A)2:3:4 (B)3:2:4(C)4:3:2 (D)4:2:3(10)如图2-88,已知,AB/CD/EF,BC/AD,AC平分BAD,那么图中与AGE相等的角有( )(A)5个 (B)4个 (C)3个 (D)2个2填空题(1)三条相交直线交于一点得6个角,每隔1个角的3个角的和是_度(2)A和B互为邻补角,A:B=9:6,则A=_,B=_.(3)如果1和2互补,2比1大,则1=_,2_.(4)如图2-89,已知AB/CD,EF分别截AB、CD于G、H两点,GM平分AGE,HN平分
13、CHG,求证:GM/HN证明: _/_( ) ,AGE=CHG( )又GM平分AGE( ) 1=_( )_平分_( ), 2=_( ),则GM/HN( )(5)如图2-90,已知,1=,2=,则3=_,4=_.(6)如图2-91,1=2,3=2, 1=3( )1=3, 1+2=3+2( ),即BOD=AOC,AOC=BODAOC2=BOD2( ),即3=1(7)如图2-92,已知,AB、AC、DE都是直线,2=3,求证:1=4证明:AB、AC、DE都是直线( ),1=2,3=4( )2=3( ),1=4( )(8)如图2-93,OBC=OCB,OB平分ABC,OC平分ACB,求证:ABC=AC
14、B证明:OB平分ABC( ),ABC=2OBC( )OC平分ACB( )ABC=2OCB( )OBC=OCB( ),2OBC=2OCB( ),即ABC=ACB,(9)如图2-94,ABBC,1=2,3=4,求证CDBC,证明:1=2,3=4( )1+3=2+4( ),即ABC=BCDABBC( ) ABC=( )BCD=( ), CDBC( )(10)如图2-95,1=3,AC平分DAB,求证:AB/CD证明:AC平分DAB( ),1=3( )1=2( ),3=2( ),AB/CD( )3 计算题提升题1.如图2-96,已知,1=,2=,求x和y 的度数 2.如图2-97,已知AMF=BNG=
15、,CMA=求MPN的度数 3.如图2-98,已知B=,过ABC内一点P作PE/AB,PF/BC,PHAB求FPH的度数 4.如图2-99,已知AE/BD,1=32,2=求C 5.如图2-100,OBOA,直线CD过O点,AOC=求DOB的度数 解法发散 1已知AB/CD,试问B+BED+D=(用两种以上方法判断)2如图2-101,已知BED=ABE+CDE,那么AB/CD吗?为什么?(用四种方法判断) 变更命题发散1如图2-102,在折线ABCDEFG中,已知1=2=3=4=5,延长AB,GF交于点M那么,AMG=3,为什么? 2.如图2-103,已知AB/CD,1=2试问BEF=EFC吗?为
16、什么?(提示:作辅助线BC) 分解发散如图2-104,AB/CD,在直线,AB和CD上分别任取一点E、F(1)如图2-104,已知有一定点P在AB、CD之间,试问EPF=AEP+CFP吗?为什么?(2)如图2-105,如果AB、CD的外部有一定点P,试问EPF=CFPAEP吗?为什么?(3)如图2-106,AB/CD,BEFGD是折线,那么B+F+D=E+G吗?简述你的理由转化发散1判断互为补角的两个角中,较小角的余角等于这两个互为补角的差的一半2已知点C在线段AB的延长线上,AB=24cm,BC=AB,E是AC的中点,D是AB的中点,求DE的长迁移发散平面上有10条直线,其中任何两条都不平行
17、,而且任何三条都不经过同一点,这10条直线最多分平面为几个区域?综合发散1线段AB=14cm,C是AB上的一点,BC=8cm,又D是AC上一点,AD:DC=1:2,E是CB的中点,求线段DE的长2如图2-107,已知1=2=3,GFA=,ACB=,AQ平分FAC,求HAQ的度数3如图2-108,已知1=2,C=D,试问A=F吗?为什么?4如图2-109,已知ADBC,EFBC,4=C,那么1=2谈谈你的理由参考答案【巩固基础训练】题型发散1(1)(D) (2)(C) (3)(C) (4)(A) (5)(D) (6)(A) (7)(B) (8)(B) (9)(A) (10)(D)2(1)如果在同
18、一平面内两条直线没有公共点,那么这两条直线平行(2)垂线段(3)40°、140°(4)垂直(5)ABC=DCE,(两直线平行,同位角相等),1=2,BCD+ABC(两直线平行,同旁内角互补)ADBC,(内错角相等,两直线平行)ADBC,(同位角相等,两直线平行)(6)(等量代换),ABEF,(内错角相等,两直线平行),(已知),2+3=180°,CDEF(如两条直线都和第三条直线平行,那么这两条直线也互相平行)(7)1和2是同位角1=2,则DEAC(同位角相等,两直线平行);直线DE、AC被直线BC所截,因此DEAC,3=4(两直线平行,同位角相等)(8)(角平分
19、线定义) 同理 (等式性质)又ABCD(已知),ABC+BCD=180°(两直线平行,同旁内角互补),1+2=90°(等量代换)(9)如果B=FGC,则ABFG,因为同位角相等,两直线平行如果BEG=EGF,则ABFG,因为内错角相等,两直线平行如果AEC+EAF=180°,则EGAC,因为同旁内角互补,两直线平行(10)B=BCFCFDE(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)D=DCF(两直线平行,内错角相等)3(1)AD、BC与AB相交,DAB与4是同旁内角,2+3+4=DAB+4=180°ADBC(同旁内角互补,两直线平行)同
20、理,1+2+5+EAC+5=180°,AEBCAD、AE在同条直线上(经过直线外一点,有条而且只有一条直线和这条直线平行)则AE、AD在A点处形成一个平角,故1+2+3=180°(2)50°,50° (3)12° (4)25°,85°纵横发散1BDEC(已知),DBC+C=180°(两直线平行,同旁内角互补)又C=D(已知),DBC+D=180°(等量代换)故ACDF(同旁内角互补,两直线平行)21=2(已知),ABCD(同位角相等,两直线平行),BMN+DNM=180°(两直线平行,同旁内角互
21、补)3+4=(180°-BMN)+(180°-DNM)=360°-180°=180°(等量代换)解法发散1(1)通过同位角相等,判断两直线平行(2)通过两条直线都和第三条直线垂直来判断这两条直线平行解法1 如图2-1,EFAB(已知),1=90°(垂直的定义)同理,3=90°,1=3又ABCD(已知),1=2(两条直线平行,同位角相等),2=3(等量代换)EFMN(同位角相等,两直线平行)解法2 EFAB(已知),1=90°(垂直的定义)又ABCD(已知),1=2=90°(两直线平行,同位角相等),EFC
22、D(垂直的定义),又MNCD(已知),EFMN(如果两条直线都和第三条直线垂直,那么这两条直线平行)2解法1 2=4,1=21=4ab(同位角相等,两直线平行)解法22=4,1=3(对顶角相等)又1=2,3=4ab(内错角相等,两直线平行)解法3 1+5=180°(平角定义),1=2,2+5=180°,又2=4(对顶角相等),4+5=180°ab(同旁内角互补,两直线平行)变更命题发散151°2(1)30°;(2)平行,根据内错角相等,两直线平行385°4因为1和4是对顶角,所以1=4,又因为1=2=3,所以4=2,4=3直线AB,C
23、D被EF所截,2和4是同位角,且4=2,所以,ABCD同理,由4=3,可推知EFMN51=6,2=7(对顶角相等),又1+2=180°(已知),6+7=180°(等量代换)ABCD(同旁内角互补,两直线平行),4=5(两直线平行,内错角相等)而3+5=180°(平角的定义),3=95°(已知),5=85°(等式性质),故4=85°(等量代换)6x=125°,y=72°7由题意,1是3的余角,而2与3余角互补,故1+2=180°,于是,所以3=5=180°-4=180°-115°
24、;=65°转化发散1分析 把判断两条直线垂直问题转化为判断两条直线平行问题理由如下:AEF=B,EFBC,FEC=1又FEC=GHB,GHB=1,GHCEGHAB,CEAB2分析 本题将证明两条直线垂直的问题转化为证明两条直线平行的问题理由如下:ADE=B(已知),DEBC(同位角相等,两直线平行),BCD=EDC(两直线平行,内错角相等)又EDC=GFB(已知),BCD=GFB(等量代换),FGCD(同位角相等,两直线平行)又FGAB(已知),故CDAB(如果一条直线和两条平行线中的一条垂直,那么,这条直线也和另一条垂直)分解发散如图2-2,过M作MNAB(过直线外一点有且只有一条
25、直线平行于已知直线),ABCD(已知),MNCD(平行于同一条直线的两条直线平行)2=EMN(两直线平行,内错角相等)4=NMF而1+2+3+4=180°,1=2,3=4,EMF=90°综合发散1已知:如图2-3,ABCD,BMN与MND是一对同旁内角,MG,NG分别是两个角的角平分线求证:MGNG证明:ABCD(已知),BMN+MND=180°(两直线平行,同旁内角互补)又MG、NG为角平分线(已知),(角平分线定义),MGN=90°MGNG2已知1=2,3=4,EMFN,求证:ABCD如图2-4,MEFN,2=3(两直线平行,内错角相等)又1=2,3
26、=4,1=4,1+2=3+4即AEF=DFE故ABCD(内错角相等,两直线平行)348.1cm5解ABCD(已知),1=2(两直线平行,内错角相等),A+ADC=180°(两直线平行,同旁内角互补),即A+ADB+2=180°ADDB(已知),ADB=90°(垂直的定义),A+2=90°(等量减等量,差相等),A+1=90°(等量代换),1与A互余(互余的定义)【提高能力测试】题型发散1(1)(C) (2)(D) (3)(C) (4)(A) (5)(C)(6)(A) (7)(A) (8)(C) (9)(B) (10)(A)2(1)180(2)1
27、08°,72°(3)85°,95°(4)ABCD(已知),两直线平行,同位角相等(已知)(角平分线定义)HN平分CHE(已知),(角平分线定义);1=2(等量代换),同位角相等,两直线平行(5)3=95°,4=85°(6)(等量代换)(等量之和相等)(等量之差相等)(7)(已知),(对顶角相等),(已知),(等量代换)(8)(已知),(角平分线定义)(已知),(角平分线定义)(已知),(等量的同倍量相等)(9)(已知),(等量之和相等)(已知),(垂线定义)(等量代换),(垂线定义)(10)(已知)(角平分线定义)(已知),(等量代换
28、)(内错角相等,两直线平行)3(1)80°,100°(2)50°(3)30°(4)28°(5)OBOA(已知),AOB=90°(垂直的定义)又AOC=20°(已知),BOC=AOB-AOC=90°-20°=70°(等式性质)又DOC是一直线(已知),DOB+BOC=180°(平角的定义),DOB=110°(等式性质)4略解法发散1解法1 如图2-5,从E点作EFABB+BEF=180°(两直线平行,同旁内角互补)又ABCD(已知),EFCD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),FED+D=180°(两直线平行,同旁内角互补),B+BEF+FED+D=360°,即B+BED+D=360°解法2 如图2-6,从E点作EFAB,则1=B(两直线平行,内错角相等)又ABCD(已知),EFCD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),2=D(两直线平行,内错角相等)1+BED+2=360°(周角的
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 门诊预约诊疗考核制度
- 煤矿化验员考核制度
- 社区救灾工作考核制度
- 保l洁质量考核制度
- 董事会绩效考核制度
- 电子代工厂考核制度
- 口腔护士消毒考核制度
- 社区服务站考核制度
- 煤矿职业卫生考核制度
- 反窃电工作考核制度
- 探秘世界气候解码甘肃生态-基于核心素养的初中地理深度教学设计
- 非标压力容器培训课件
- 2026-2031中国槟榔市场发展策略及投资潜力可行性预测报告
- 2026版二建《建设工程法规及相关知识》精讲课程讲义(完整打印版)
- 2025年江苏省常州中考物理试题
- 传感器应用技术 课件全套 梁长垠 项目1-8 传感器认知与测量系统搭建- 无线传感器网络应用电路设计与调试
- 2025年复旦大学文科试题及答案
- 【北师大版】六年级数学上册寒假作业
- 村规民约用水管理制度
- 亿安科技作手教你炒股系列
- 2022年上海外国语大学硕士生培养方案:英语语言文学

评论
0/150
提交评论