高一数学二次函数的最值问题

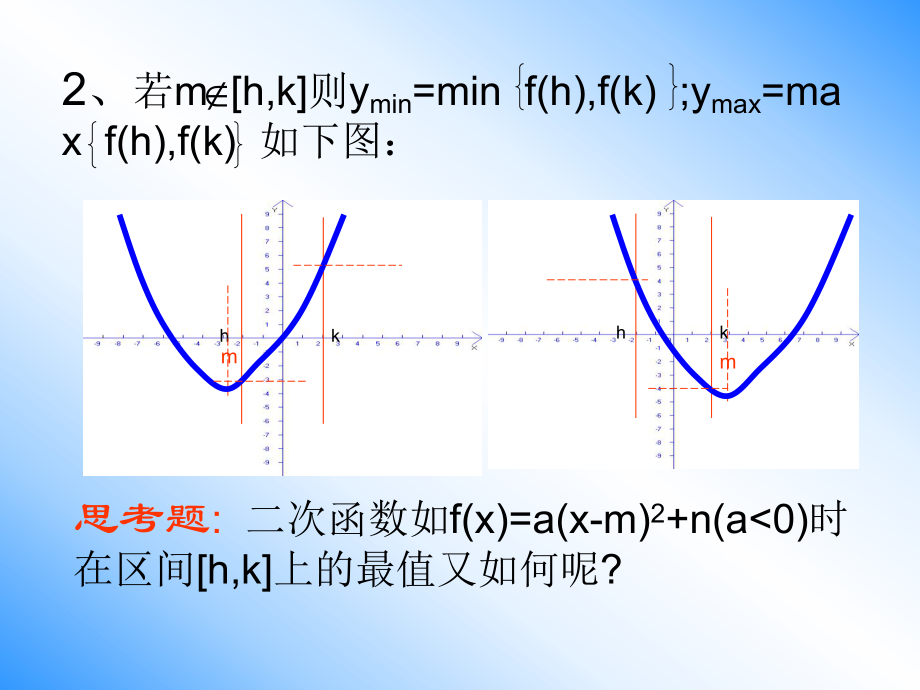
1、二次函数的最值二次函数的最值问题二次函数的最值问题重点 掌握闭区间上的二函数的 最值问题难点 了解并会处理含参数的二 次函数的最值问题核心 区间与对称轴的相对位置思想 数形结合 分类讨论 复习引入顶点式:y=a(x-m)+n(a 0)两根式:y=a(x-x1)(x-x2)(a 0)一般式:y=ax2+bx+c(a 0) =a(x+ )2+a0时 开口向上 x = -ymin=a0)时在区间h,k上的最值问题则有：1、若mh,k则ymin=n;ymax=max f(h),f(k)如下图：mhknhkm2、若m h,k则ymin=min f(h),f(k) ;ymax=max f(h),f(k)

2、如下图： 思考题: 二次函数如f(x)=a(x-m)2+n(a0)时在区间h,k上的最值又如何呢?hkmhkm1.若mh,k则ymax=n;ymin=min f(h),f(k)如下图：mhkhkmnhkmhkm2、若m h,k则ymax=max f(h),f(k) ;ymin=max f(h),f(k) 如下图： 即当x=-1时ymin=-4 ;当x=2时ymax=f(2)=5练习1 求函数y=x2-2x-3且x 0,3的最值？例题1 已知函数y=x2+2x-3 且x -2，2,求函数的最值？ 解析：函数配方有 y=(x+1)2-4如右图例题2已知函数y=-x2-2x+3且x 0，2,求函数的

3、最值？ 解析：y= -x2-2x+3 = -(x+1)2+4因为x 0，2如右图 则ymax=f(0)= 0+0+3=3 ymin=f(2)= -4-4+3=-5练习2 求函数y=-x2+2x+3且x 0,2的最 值？二、含参变量的二次函数最值问题 解析：因为函数y=x2+2ax+3 =（x+a)2+3-a2的对称轴为x=-a。要求最值则要看x=-a是否在区间-2，2之内，则从以下几个方面解决如图：1、轴动区间静 2、轴静区间动例3：求函数y=x2+2ax+3在x -2,2时的最值？-a 当-2-a0时 f(x) max=f(2)=7+4a (0a 2) f(x) min=f(-a)=3-a2

4、 当-a-2 时 f(x) max= f(2)=7+4a (a2) 时 f(x) min=f(-2)=7-4a 当0-a2时 f(x) max=f(-2)=7-4a (-2 a 0) f(x) min=f(-a)=3-a2 当 -a2 时 f(x) max=f(-2)=7-4a (a -2) f(x) min=f(2)=7+4a 则由上图知解为: 例4 求函数y=x2-2x-3在xk,k+2的函数的最值?解析解析: 因为函数 y=x2-2x-3=(x-1)2-4的对称 轴为 x=1 固定不变,要求函数的最值, 即要看区间k,k+2与对称轴 x=1的位 置,则从以下几个方面解决如图:X=1kK+

5、2则由上图知解为: 当k+21(k -1)时 f(x)max=f(k)=k2-2k-3 f(x)min=f(k+2)=k2+2k+3 当 k 1 k+2 时 f(x)max=maxf(k),f(k+2) (-1 k 1) f(x)min=f(1)=-4 当k 1 时 f(x) max=f(k+2)=k2+2k+3 f(x) min=f(k)=k2-2k-3 例5 求函数y=x2-2x-3在x-3,m函数的最值?解析解析:因为函数 y=x2-2x-3=(x-1)2-4 的对称轴为x=1 固定不变,要求函数的最值, 即要根据具体的区间 -3,m 与对称轴x=1的位置,则从以下两个方面解决如图:则由上图知解为:当-3m1时 f(x)max=f(-3)=12 f(x)min=f(m)=m2+2m+3 当 1m 时 f(x)max=maxf(-3),f(m) f(x)min=f(1)=-4练习3 求函数y=x2-2ax-3在x0,3的最值？ 练习4 求函数y=