【课件】第七章综合复习：复数课件（人教A版2019必修第二册）

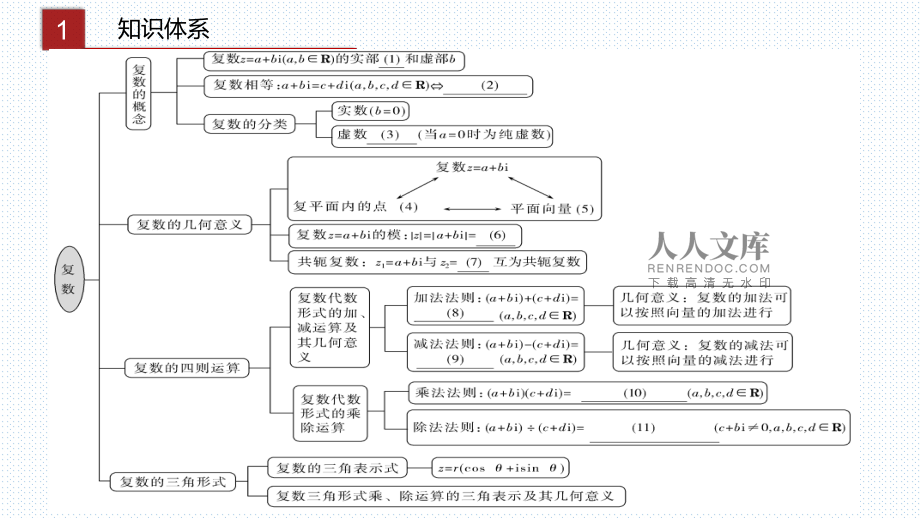
1、人教A版2019高中数学必修第二册第七章 复数章节复习1知识体系2知识点梳理1复数复数(3)复数相等：复数相等：abicdi_(a，b，c，dR)ac且且bd(4)共轭复数：共轭复数：abi与与cdi共轭共轭_(a，b，c，dR)ac，bd(5)模：模：2知识点梳理2复数复数的几何意义的几何意义2知识点梳理3复数复数的运算的运算(1)复数的加、减、乘、除运算法则复数的加、减、乘、除运算法则设设z1abi，z2cdi(a，b，c，dR)，则则加法：加法：z1z2(abi)(cdi)_；(ac)(bd)i减法：减法：z1z2(abi)(cdi)_；(ac)(bd)i乘法：乘法：z1z2(abi)(

2、cdi)_；(acbd)(adbc)i2知识点梳理(2)复数加法的运算律复数加法的运算律3复数复数的运算的运算 复数的加法满足复数的加法满足交换律交换律、结合律结合律，即对任何，即对任何z1，z2，z3C，有，有z1z2_，(z1z2)z3_z2z1z1(z2z3)常用结论2知识点梳理abicosr sinir (cossin )ri22rabcosar sinbr 4. 复数的三角表示式其中5.复数三角形式乘法2知识点梳理6.复数三角形式的除法法则所以根据复数除法的定义，有3题型讲解考点考点1复数的有关概念复数的有关概念1已知a，bR，(ai)ib2i，则abi的共轭复数为()A2i B2i

3、C2i D2iA(ai)i1aib2ia2b1abi2i其共轭复数为2i3题型讲解解得a1.C3题型讲解C3题型讲解CD所以复数z的实部是1，虚部是2，3题型讲解方法总结(1)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题，只需把复数化为代数形式，列出实部和虚部满足的方程(不等式)组即可解决复数概念问题的方法及注意事项(2)解题时一定要先看复数是否为abi(a，bR)的形式，以确定实部和虚部3题型讲解考点2复数的几何意义1(2019高考全国卷)设复数z满足|zi|1，z在复平面内对应的点为(x，y)，则()A(x1)2y21 B(x1)2y21Cx2(y1)21 D

4、x2(y1)21所以x2(y1)21.C因为z在复平面内对应的点为(x，y)，所以zxyi(x，yR)因为|zi|1，所以|x(y1)i|1，3题型讲解C位于第三象限3题型讲解3(2021成都市诊断性检测)若复数z1与z23i(i为虚数单位)在复平面内对应的点关于实轴对称，则z1()A3i B3iC3i D3i所以z13i.z23i在复平面内对应的点为(3，1)，点(3，1)关于实轴对称的点为(3，1)，B3题型讲解z1i在复平面内所对应的点为(1，1)，在第一象限，所以D正确z1i的虚部为1AD3题型讲解方法总结1. 复数的几何意义及应用复数的几何意义及应用(1)进行简单的复数运算，将复数化

5、为标准的代数形式；(2)把复数问题转化为复平面内的点之间的关系，依据是复数abi(a，bR)与复平面上的点(a，b)一一对应2解解与复数的几何意义相关问题的一般步骤与复数的几何意义相关问题的一般步骤3题型讲解考点3复数代数形式的运算设复数zabi(a，bR)，C3题型讲解D方法一i方法二i3题型讲解z(ai)(32i)3a2(2a3)i3a21，解得a1虚部为2a32(1)35z在复平面内对应的点为(1，5)，位于第三象限ACD3题型讲解所以|z1z2|的最小值为3.B3题型讲解方法总结(1)复数的乘法：复数的乘法类似于多项式的乘法运算，可将含有虚数单位i的看作一类同类项，不含i的看作另一类同类项，分别合并即可(2)复数的除法运算是分子、分母同乘以分母的共轭复数，即分母实数化 复数代数形式运算问题的解题策略3题型讲解考点4复数三角表示3题型讲解3题型讲解3题型讲解3题型讲解随堂训练A3题型讲解z22iB(z2)izz(i1)2i3题型讲解设zabi(a，bR)，所以abi(1b)ai，A3题型讲解设zabi，a，bR，则由z21216i，得a2b22abi1216i，C3题型讲解ABC3题型讲解 本节知识主要考查复数的本节知识主要考查复数的基本概念基本概念(复数的实部、复数的实部、虚部、共轭复数、复