数量行测专项笔记

1、专项-数量 2（讲义）公式类【例 1】（2017 联考）某准备扩建一矩形花圃，若将矩形花圃的长和宽各增加 4 米，则新矩形花圃的面积比原来的面积增加了 40 平方米。那么，形花圃的周长是多少？A.12 米B.24 米C.32 米D.40 米【例 2】（2012 国考）连接正方体每个面的中心一个正八面体（如下图所示）。已知正方体的为 6 厘米，问正八面体的体积为多少立方厘米：A.B.C.36D.72【例 3】（2015 联考）一只挂钟的秒针长 30 厘米，分针长 20 厘米，当秒针的顶点走过的弧长约为 9.42，分针的顶点走过的弧长约为多少厘米？A.6.98B.10.47C.15.70D.23.

2、55【例 4】（2014 吉林）广场举行放风筝比赛，老年组老王、老黄三位选手同场竞技，评委测量各人放出的风筝线长分别为 60 米、50 米、40 米，1风筝线与地平面所分别为、，假设风筝线看作是拉直的，则三位选手放风筝最高的是：A.老王B.C.老黄D.不能确定【例 5】（2015 国考）现要在一块长 25 公里、宽 8 公里的长方形区域内设置哨塔，每个哨塔的监视半径为 5 公里。如果要求整个区域内的每个角落都能被监视到，则至少需要设置多少个哨塔：A.7B.6C.5D.4结论类特殊性质【例 1】（2016）小王近期正在装修新房，他计划将长 8 米、宽 6 米的客厅按右图所示分别在各连线形成的四边

3、形内铺设不同花色的瓷砖，则需要为最里侧的四边形铺设多少平方米的瓷砖？（ ）A.3B.6C.12D.242【例 2】（2017 联考）如右图所示，甲和面积为的半圆形游泳池内游泳，他们分别从位置 A 和 B 同时出发，沿直线同时游到位置 C。若甲的速度为乙的 2 倍，则原来甲、相距：A.米B.15 米C.米D.18 米【例 3】（2017 联考）妈妈为了给过生日的一个惊喜，在一底面半径为20cm、60cm 的生日帽内藏了一个圆柱形盒。为了不让事先发现盒，该盒的侧面积最大为多少？A.B.C.D.枚举归纳【例 4】（2016 吉林）用直线切割一个有限平面，后一条直线与此前每条直线都要产生新的交点，第

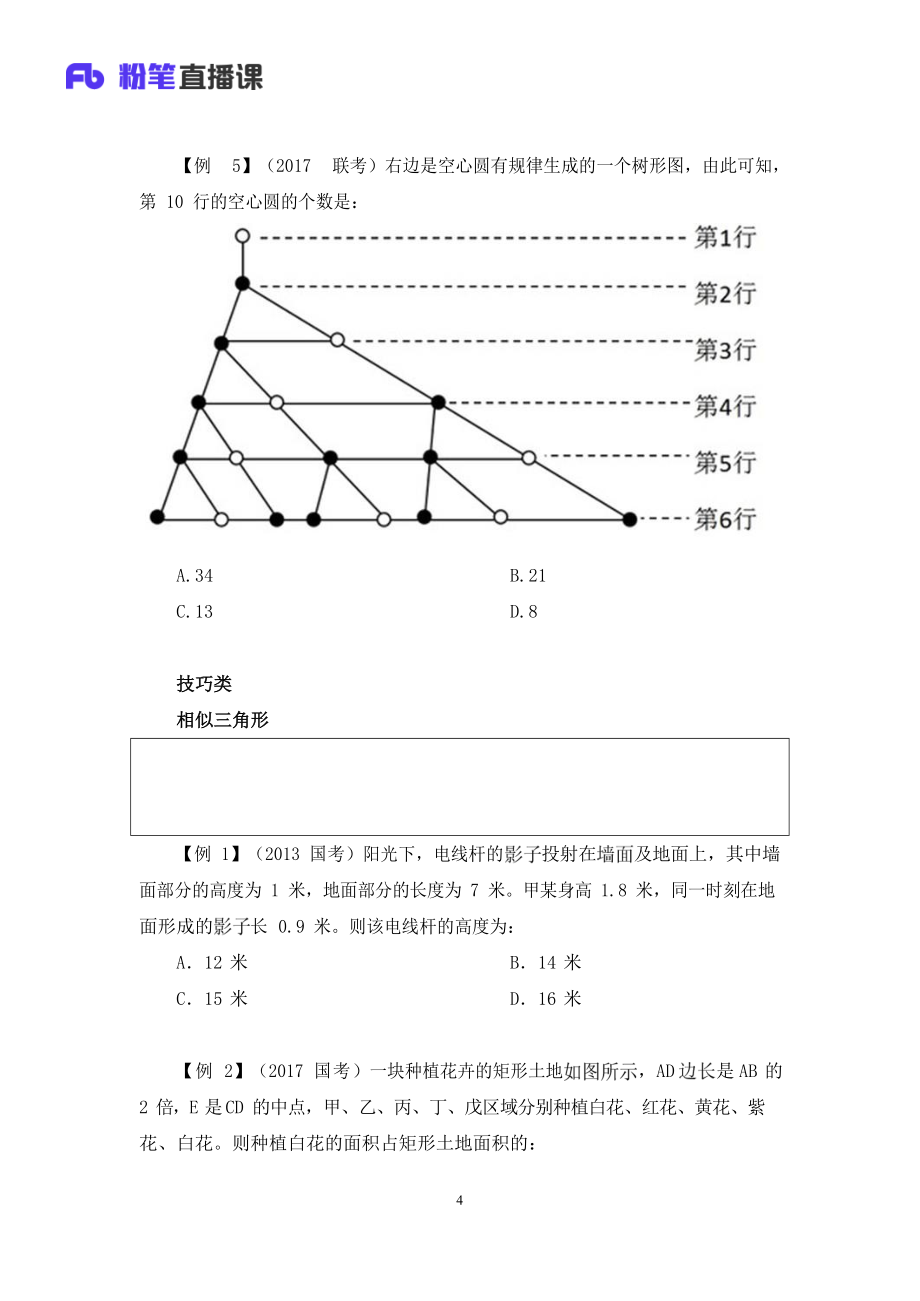
4、1 条直线将平面分成 2 块，第 2 条直线将平面分成 4块，第 3 条直线将平面分成 7 块，按此规律将平面分为 46 块需要：A.7 条直线B.8 条直线C.9 条直线D.10 条直线3【例 5】（2017 联考）右边是空心圆有规律生成的一个树形图，由此可知，第 10 行的空心圆的个数是：A.34B.21C.13D.8技巧类相似三角形【例 1】（2013 国考）阳光下，电线杆的投射在及地面上，其中墙面部分的高度为 1 米，地面部分的长度为 7 米。甲某身高 1.8 米，同一时刻在地面形成的长 0.9 米。则该电线杆的高度为：A12 米B14 米C15 米D16 米【例 2】（2017 国考

5、）一块种植花卉的矩形土地，AD是 AB 的2 倍，E 是 CD 的中点，甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。则种植白花的面积占矩形土地面积的：4A.B.C.D.最短路径【例 1】（2017 吉林）悟空与二郎神在离地面 1 米的空中决斗，两人相距 2米，悟空想用直接偷袭二郎神，为了不引起对警觉，必须在地面反弹一次再进行，则到神的位置所走的最短距离为：A.米B.米C.米D.米5【例 2】（2017 江苏）某市规划建设的 4 个小区，分别位于直角梯形 ABCD的 4 个顶点处（如图），AD4 千米，CDBC12 千米。欲在 CD 上选一点 S 建，使其与 4 个小区的直线距离

6、之和为最小，则 S 与 C 的距离是：A.3 千米B.4 千米C.6 千米D.9 千米【例 3】（2017 联考）如下图所示，某条河流一侧有 A、B 两家工厂，与河岸的距离分别为 4km 和 5km，且 A 与 B 的直线距离为 11km。为了处理这两家工厂的污水，需要在距离河岸 1km 处建造一个污水处理厂，分别铺设排污管道连接 A、B 两家工厂。河岸是一条直线，则排污管道总长最短是：A.12kmB.13kmC.14kmD.15km【例 4】（2017联考）如右图所示，一个为 10 厘米的正方体木块，点 E、F 分别是、的中点，6是用蜂蜜画的一条线段，一只蚂蚁在点 F 处，要想沿正方体表面最

7、快到达蜂蜜所在线段，它所爬行的最短距离是多少厘米？A.B.C.D.7专项-数量 2（笔记）【注意】几何部分会涉及到基础知识、公式类、结论类、技巧类题目。其中基础知识是给大家补充的知识点，公式类、结论类、技巧类是具体的题型。题型分为三种，第一种是公式类题，只要拿到公式就可以解题，这类题目难度不高；第二种是结论类题，用公式可以解出来，但是比较耗时，如果记住一些结论、特殊的定理，就可以很快解题；第三种是技巧类题目，需要根据题目的解题技巧去做，这也是越来越热门的考法，2017 年很多省都有考到，如最短路径的考查。【知识点】几何公式：几何类在考试中占的比例比较特殊，在 2016 年及以前考查的比较少，但

8、是在 2017 年爆发性的考了 4-5 道题目，所以我们要好好复习几何问题。1.周长：（1）正方形：4a。（2）长方形：2（a+b）。（3）圆形：2R。（4）弧长：2R*n°/360°（考的比较少，建议大家记一下）。2.面积：（1）正方形：a²。（2）长方形：ab。（3）三角形：ah/2。8（4）圆形：R²。（5）梯形：（a+b）/2*h（不常考）。（6）菱形：对角线乘积/2。菱形是类似水晶一样的形状，菱形的对角线互相垂直，四条边相等。正方形是一种特殊的菱形，菱形面积为对角线乘积/2。例：一个正方形的对角线长度为 10，问这个正方形的面积是多少？答：对角

9、线长度是 10，可以先算出正方形的再平方去计算，但是比较繁琐。直接记住公式算，面积=对角线乘积/2=10*10/2=50。3.表面积：（1）正方体：6a²（考的比较多，每个面的平方乘以 6）。（2）长方体：2（ab+bc+ac）。（3）圆柱体：2R²+2Rh（2017 年联考考到了圆柱体的侧面积，建议大家复习一下）。例：把可乐罐近似看成一个圆柱体，上下有两个圆，面积为 2R*2；把圆柱体展开后是一个长方形，长度为 2R，宽是可乐罐的高 h，长方形面积为 2Rh，因此圆柱体表面积为 2R²+2Rh。（4）球体：4R²（考的非常少，有精力的同学可以记）。4.

10、体积：（1）正方体：a³。（2）长方体：abc。（3）柱体：Sh（必须掌握）。（4）椎体：Sh/3。圆柱体镂空出一个圆柱体，它们的底面积和高都是一样的，它们的体积为 3：1 的。（5）球体：4R³*3（考的比较少，陕西省的同学可以做一做）。补充 1：正六边形：一种特殊的六条边形，6 条边相等。正六边形的面积求法：一：把正六边形切割、平移成规则图形，但是求的时候比较难算。二：把各对角连线，每个角原来是 120°，连线后就会被分成两个 60°，每个是 a，有 6 个边，即六个小等边三角形。9【拓展】一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形

11、的：A.2倍B.1.5 倍C.3倍D.2 倍【】拓展.正三角形和一个正六边形周长相等，说明周长既是 3 的倍数，也是 6 的倍数，用赋值法。设6，则正三角形的为 2，正六边形的边长为 1。正六边形为 6 个为 1 的正三角形，把为 2 的正三角形各连结，变成 4 个为 1 的三角形。即 6/4=1.5 倍。【选 B】【注意】三角形连结各，其面积也会四等分。补充 2：多边形的角度：三角形内角和 180°，四边形内角和为 360°，五边形内角和为 540°。n 边形内角和=180（n-2）度。例：六边形的内角=（6-2）*180°/6 个角=120°

12、;。n 边形外角和=360 度。把一个内角的延伸，会形成一个外角，内角和外角平角（180°）。例：正六边形会形成 6 个外角，6 个 60°为 360°。每一条线都是 180°的10直线，内角占了 120°，所以外角为 60°。有时候出题只给出外角，不给内角，我们记住固定结论，就可以很快解题。【拓展】（2014 年河北）科技馆为某编制一段程序，如果在平地上按照图中所示的步骤行走，那么该所走的总路程为多少米？A.20 米B.15 米C.12 米D.10 米【】拓展.开始的时候站在原点，向前走一米，向右转 18°，机器人没有回到

13、原点，再继续上一步骤，往前走一米，向右转 18°，始终都会走一米，转 18°，要转一大圈之后才会结束。题目给出的 18°为外角，已知外角和为 360°，则 360/°18°=20 个外角=20 个内角=20 条边，每条是 1米，总路程=20*1=20 米。【选 A】补充 3：等比例放缩、几何最值：若将一个图形尺度（可以理解为、半径）扩大至 N 倍，则：111.对应角度不变（图形放大、缩小，角度不变）。2.周长变为原来的 N 倍（原来周长是 a+b+c，现在是 2a+2b+2c），扩大了 N-1倍（比如原来周长是 100，现在是 400

14、，是扩大到原来的 4 倍，扩大了 3 倍）。3.面积变为原来的 N²倍（长*n，宽*n，面积为长*宽*n*n），扩大了 N²-1 倍。4.体积变为原来的 N³倍（长*n，宽*n，高*n，体积为长*宽*高 n*n*n），扩大了 N³-1 倍。5.记忆：周长是一维，只有，就是乘以一次方倍；面积是二维，有长、宽，就是乘以二次方倍；体积是三维，有长、宽、高，就是乘以三次方倍。【拓展 1】圆形的周长扩大至原来的 2 倍，它的面积比原来增大了（）。A.1 倍B.2 倍C.3 倍D.4 倍【】拓展 1.圆形周长是 N 倍，面积是 N²倍，N=2，周长是一维，

15、面积是二维，面积变为原来的 N²=4 倍，增大了 N²-1=4-1=3 倍。【选 C】【拓展 2】正六面体的表面积增加 96%，棱长增加多少：（）A.20%B.30%C.40%D.50%【】拓展 2.表面积增加 96%，即变为原来的 N²=1+96%=1.96 倍，N=1.4。增加了 N-1=1.4-1=0.4=40%。【选 C】【知识点】几何最值：1.给一条线，周长固定，围成一个平面图形，越接近圆，面积越大，圆的面积最大。2.给一块布，表面积固定，越接近球，体积越大，球的体积最大。3.记忆：圆和球是最省材料的，给出同样的长度，圆可以围成最大的面积；给出同样的表面

16、积，球可以围出最大的体积。4.例：同样的表面积，以下哪个围出的体积最大的？A.四面体B.六面体12C.正十二面体D.正二十面体答：表面积相同越接近，体积越大，正二十面体最接近。【选 D】公式类【例 1】（2017 联考）某准备扩建一矩形花圃，若将矩形花圃的长和宽各增加 4 米，则新矩形花圃的面积比原来的面积增加了 40 平方米。那么，形花圃的周长是多少？A.12 米B.24 米C.32 米D.40 米【】例 1.矩形（长方形）正方形，长宽各加 4 米。设长、宽分别为 a、b，原来面积=a*b，现在面积=（a+4）*（b+4），则有（a+4）*（b+4）=ab+40，ab+4（a+b）+16=a

17、b+40，a+b=6，原来的周长=2*6=12。【选 A】【例 2】（2012 国考）连接正方体每个面的中心一个正八面体（如下图所示）。已知正方体的为 6 厘米，问正八面体的体积为多少立方厘米：A.B.C.36D.72【】例 2.一：本题在 2013 年作为联考题出现过。正方体、长方体都可以用公式求，但是本题的正八面体是不规则图形，试着拆分一下，把正八面体从上下或者左右剖开，分成两个对称的椎体。V 八面体=V 锥*2，求OABCD 的体积即可。V 锥=1/3*SABCD*h，O 到 ABCD 的高度 h 为 6/2=3，V 八面体=1/3*SABCD*3*2=2SABCD。俯视看，ABCD 连

18、结各之后为菱形，则 SABCD=1/2*6*6=18，V 八面体=2*18=36。13二：记住结论，“正方体内接的正八面体，体积=a³/6”。a 为正方体的，a=6，V 八面体=2*18=36。【选 C】【注意】把正方形各相连，面积会减少为原来的一半，可以求出SABCD=1/2*6*6=18。【知识点】弧长公式：弧长=n°/360°*2R=nr/180。例：求从 A 到 B 对应的弧长？AB=AB 占圆周的比重*圆周长=AB 所占的角度/360°，弧长之比就是对应的角度之比。14【例 3】（2015 联考）一只挂钟的秒针长 30 厘米，分针长 20 厘米

19、，当秒针的顶点走过的弧长约为 9.42，分针的顶点走过的弧长约为多少厘米？A.6.98B.10.47C.15.70D.23.55【】例 3.秒针弧长=nR/180=n秒*30/180=9.42米，分针=弧长 nR/180=n 分*20/180=（）米，两者做比较形成一个比例，即 3n 秒/2n 分=9.42米/（）米，此时只要知道分针和秒针的角度即可。在时间相同的情况下，比如一分钟，秒针走一圈 360°，分针走一格 6°，所以 n 秒/n 分=360°/分÷360°/6°分=360°/6°=60。因此 60*3/2

20、=9.42 米/（），（）=9.42/90=10+厘米。【选 B】【注意】1.弧长=nr/180 比较时，、180数，只比较 n*R 即可。2.拓展：（1）分针与时针的角度之比。1 小时分针转一圈为 360°，时针转一格为 360°/12=30°，分针与时针的角度之比=12：1。（2）秒针与时针的角度之比。1 小时秒针转 60 圈为 60*360°，时针转一格为 360°/12=30°，秒针与时针的角度之比=720：1。3.问分针、秒针扫过的面积比？扫过的面积为扇形，即两个扇形的面积比。S 扇形=n°/360°*R

21、²，面积与 n°和 R²的面积有有关。15【例 4】（2014 吉林）广场举行放风筝比赛，老年组老王、老黄三位选手同场竞技，评委测量各人放出的风筝线长分别为 60 米、50 米、40 米，风筝线与地平面所分别为、，假设风筝线看作是拉直的，则三位选手放风筝最高的是：A.老王B.C.老黄D.不能确定【】例 4.当角度用的时候为 180°，/6、/4、/3 分别为 30°、45°、60°。的 sin、cos 等不用记，只要记住 30°对应的直角边是斜边的 1/2；45°对应的斜边为 22；60°对应的

22、是斜边的3/2。一：直接算。老王风筝线为 60 米，高度 h=30 米；风筝线为 50 米，高度 h=252=25*1.41435+米；老黄风筝线为 40 米，h=203=20*1.73234.6米，最高的是。二：化简。把所有的数都化到根号内，老王 h= ；h=625*2= 25 ；老黄 h=4 *3= 2 ，最高的是。三：算开同学可以直接用高度的平方比较。即老高 h²=900；h²=1250；老黄 h²=1200，最高的是。【选 B】【注意】2=1.1414，3=1.732，5=2.236，6=2.449。【例 5】（2015 国考）现要在一块长 25 公里、宽

23、 8 公里的长方形区域内设置哨塔，每个哨塔的监视半径为 5 公里。如果要求整个区域内的每个角落都能被监视到，则至少需要设置多少个哨塔：16A.7B.6C.5D.4【】例 5.要使哨塔最少，就要让哨塔监视的面积尽量大。让哨塔在监视和监视的区域“擦肩而过”，第一个哨塔与长方形外接，第二个哨塔要套住第一个哨塔。宽度是 8，从圆心横向做垂线，等腰三角形的分角和底边，宽度为 4，根据勾股定理（a²+b²=c²），“股四”，则3。哨塔横向覆盖长度为 6，宽度，4 个圆覆盖 24 公里，剩下 25-24=1 公里，还需要 1 个哨塔，因此至少需要 5 个哨塔。【选 C】【注意】

24、满足勾股定理的数为勾股数，其中（3、4、5）；（5、12、13）这两对是常考的勾股数，还有它们的延伸（6、8、10）等。【汇总】1-5：ACBBC17【小结】几何公式：1.规则图形：求长度、面积、表面积、体积等，用几何公式计算。2.不规则图形：可以通过割补平移转化为规则图形（如正八面体、正六边形），也可以反向求解。结论类特殊性质【例 1】（2016）小王近期正在装修新房，他计划将长 8 米、宽 6 米的客厅按右图所示分别在各连线形成的四边形内铺设不同花色的瓷砖，则需要为最里侧的四边形铺设多少平方米的瓷砖？（ ）A.3B.6C.12D.2418【】例 1.与花色无关，求面积。最外面长方形的面积为

25、 6*8=48，根据结论，最里侧面积 48*（1/2）*（1/2）*（1/2）=48*（1/8）=6。【选 B】【注意】1.连接任意四边形各，面积减半。2.连接任意三角形各，面积减少为四分之一。【拓展】给定三角形，连接各，连接 3 次以后，原来的面积是 n，则最里侧面积是 n*（1/4）³=n/64。【例 2】（2017 联考）如右图所示，甲和面积为的半圆形游泳池内游泳，他们分别从位置 A 和 B 同时出发，沿直线同时游到位置 C。若甲的速度为乙的 2 倍，则原来甲、相距：A.米B.15 米C.米D.18 米【】例 2.AC 是直径，半圆面积为 54，而 54=r²/2，则

26、 r²=108，即 r= 8。甲的速度为乙的 2 倍，同时游到 C 说明时间相同，则路程也为 2 倍，则 AC=2BC。结论：由圆上一点和圆的直径所组成的三角形一定是直角三角形，故CBA=90°，BAC=30°，AB=3r=3* 8=324=18。【选 D】【注意】由圆上一点和圆的直径所组成的三角形一定是直角三角形。反之，圆内接三角形如果是直角三角形，则其斜边一定是直径。【例 3】（2017 联考）妈妈为了给过生日的一个惊喜，在一底面半径为20cm、60cm 的生日帽内藏了一个圆柱形盒。为了不让事先发现盒，该盒的侧面积最大为多少？A.B.19C.D.【】例 3.圆

27、柱侧面积 S=2r*h。结论：要想侧面积最大，则其高度和半径均为圆锥体的一半。故圆柱的半径为 20/2=10cm，60/2=30cm，所以 S=2*10*30=600。【选 A】【注意】1.圆锥体内最大的圆柱体，其高度和半径均为圆锥体的一半。2.圆柱体内最大的圆锥体，其 S 和 h 均相同。【汇总】1-3：BDA枚举归纳【例 4】（2016 吉林）用直线切割一个有限平面，后一条直线与此前每条直线都要产生新的交点，第 1 条直线将平面分成 2 块，第 2 条直线将平面分成 4块，第 3 条直线将平面分成 7 块，按此规律将平面分为 46 块需要：A.7 条直线B.8 条直线C.9 条直线D.10

28、 条直线【】例 4.数线/面/交点等元素个数的时候常用枚举归纳法。0 条直线将平面分成 1 块，1 条直线将平面分成 2 块，2 条直线将平面分成 4 块，3 条直线将平面分成 7 块。找规律，1、2、4、7、呈等差数列，7+4=11、11+5=16、16+6=22、22+7=29、29+8=37、37+9=46，故第 9 条直线将平面分成 46 块。【选 C】【注意】此题中的直线还可换成空心圆。【例 5】（2017 联考）右边是空心圆有规律生成的一个树形图，由此可知，第 10 行的空心圆的个数是：20A.34B.21C.13D.8【】例 5.，找规律，第 1 行到第 6 行空心圆的数量分别是

29、 1、0、1、1、2、3，前两行相加等于第三行，求和数列。第 7 行是 2+3=5，第 8 行是 3+5=8，第 9 行是 5+8=13，第 10 行是 8+13=21，第 10 行的空心圆个数为 21。【选 B】【注意】此题的规律圆右下延伸出空心圆。【拓展】如果空心圆改圆，规律一样，即依次求和，第 10 行的实心圆的个数是 34 个。【汇总】4-5：CB【小结】结论类1.已知结论（例 1例 3）：利用已知结论。2.未知结论：用枚举归纳法。技巧类相似三角形【知识点】1.相似三角形指两个三角形形状相同，大小不同。2.条件：如果两个三角形有两个角相等，则两个三角形相似。3.结论：相似三角形大小成比

30、例。21【例 1】（2013 国考）阳光下，电线杆的投射在及地面上，其中墙面部分的高度为 1 米，地面部分的长度为 7 米。甲某身高 1.8 米，同一时刻在地面形成的长 0.9 米。则该电线杆的高度为：A12 米B14 米C15 米D16 米【】例 1.，投到地面上，墙上有一部分，墙上是 1 米，地面上长度是 7 米，甲身高与比为 1.8/0.9=2/1。阳光射下的角度相同，两个相似三角形，所以 h/7 米=1.8/0.9，故 h=14 米，电线杆高度为 14+1=15米。【选 C】【例 2】（2017 国考）一块种植花卉的矩形土地，AD是 AB 的2 倍，E 是 CD 的中点，甲、乙、丙、丁

31、、戊区域分别种植白花、红花、黄花、紫花、白花。则种植白花的面积占矩形土地面积的：A.3/4B.2/3C.7/12D.1/2【】例2.一：甲是白花，戊是白花，找甲和戊的面积和占总面积的比重。戊的面积一定，而甲丙两个三角形相似，则 AB/DE=6/3=2：1，相似三22角形各成比例，故是成比例的 2：1，h 甲=（2/3）*长。赋值，设长为6，宽为 3，故 h 甲=4，S 戊=1.5*6/2=4.5，S 甲=3*4/2=6，S 矩形=6*3=18，故比重为（4.5+6）/18=3.5/6=7/12。二：如果国考题目中几何题型配有图片，可以采用测量法，用尺子量长宽，得出。【选 C】【汇总】1-2：C

32、C【小结】1.判定：两角相同为相似三角形。2.结论：相似三角形各边大小成比例，同时比例。最短路径【例 1】（2017 吉林）悟空与二郎神在离地面 1 米的空中决斗，两人相距 2米，悟空想用直接偷袭二郎神，为了不引起对警觉，必须在地面反弹一次再进行，则到神的位置所走的最短距离为：23【知识点】例子：一条公路两个村庄 A 和 B，在公选 C 点，为让 A 到 C 和 B 到 C 的长度之后最短，问 C 的位置在哪里。答：对于这种不能直接连直线的题目，可以采用镜面展开计算。如 B 点沿公路投射到 B，连接 AB，则 AC+BC 最短路径转化为 AB的长度最短。A.2 2 米B. 3 米C. 2 米D.2 3 米【】例 1.到 C 和乙到 C 的最短距离。地面到乙，乙到地面的高度依然为 1 米，转化为乙的距离。甲乙=2 米，=1+1=2 米，等腰直角三角形，距离最短为2² + 2²=22米。【选 A】【注意】题干中如果出现“反弹一次”、“折返一次”的字眼，都可以采用镜面展开的计算