



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1、 第三讲 直线与圆的位置关系、圆与圆的位置关系教学目标1.掌握直线与圆的三种位置关系及其相应数量关系的特征,通过分析将直线与圆的各种位置关系转化为相应的数量关系,体会数量分析的研究方法以及量变引起质变的观点.2.掌握圆的切线的判定定理.3.理解圆与圆的位置关系及其有关概念,初步掌握圆与圆各种位置关系相应的数量关系的特征,会进行“圆与圆的位置关系”、“两圆圆心距与这两圆半径长之和或差的大小关系”这两者之间的相互转化,并能初步运用这些知识解决有关问题.4.掌握两圆相切和相交的连心线性质定理.教学重点1.直线和圆的位置关系的判定方法和性质.2.两圆的五种位置关系中的圆心距与两圆的半径之间的数量关系.
2、3.相交、相切两圆的性质及应用.教学难点1.探索直线与圆的位置关系中圆心到直线的距离与半径的大小关系并运用相关结论解决有关问题.2.探索圆和圆的位置关系中两圆圆心距与两圆半径的数量关系并运用相关结论解决有关问题.教学方法建议总结归纳,启发诱导,讲练结合,巩固优化.第一部分 知识梳理一 .直线与圆的位置关系1.直线与圆的三种位置关系如图,设O的半径为r ,圆心O到直线的距离为d,得出直线和圆的三种位置关系:(1)直线和O相离 此时:直线和圆没有公共点(2)直线和O相切 此时:直线和圆有唯一公共点,这时的直线叫做圆的切线,唯一的公共点叫做切点(3)直线和O相交 此时:直线与圆有两个公共点,这时的直
3、线叫做圆的割线lll(1)(2)(3)OOO2. 切线的判定定理经过半径的外端且垂直于这条半径的直线是圆的切线.切线的性质:(1)与圆只有一个公共点;(2)圆心到切线的距离等于半径;(3)圆的切线垂直于过切点的半径.切线的识别:(1)如果一条直线与圆只有一个公共点,那么这条直线是圆的切线.(2)到圆心的距离等于半径的直线是圆的切线.(3)经过半径的外端且垂直与这条半径的直线是圆的切线.证明直线是圆的切线的两种情况:(1)当不能说明直线与圆是否有公共点时,应当用“圆心到直线的距离等于半径长”来判定直线与圆相切.(2)当已知直线与圆有公共点时,应当用判定定理,即“经过半径外端且垂直于半径的直线是圆
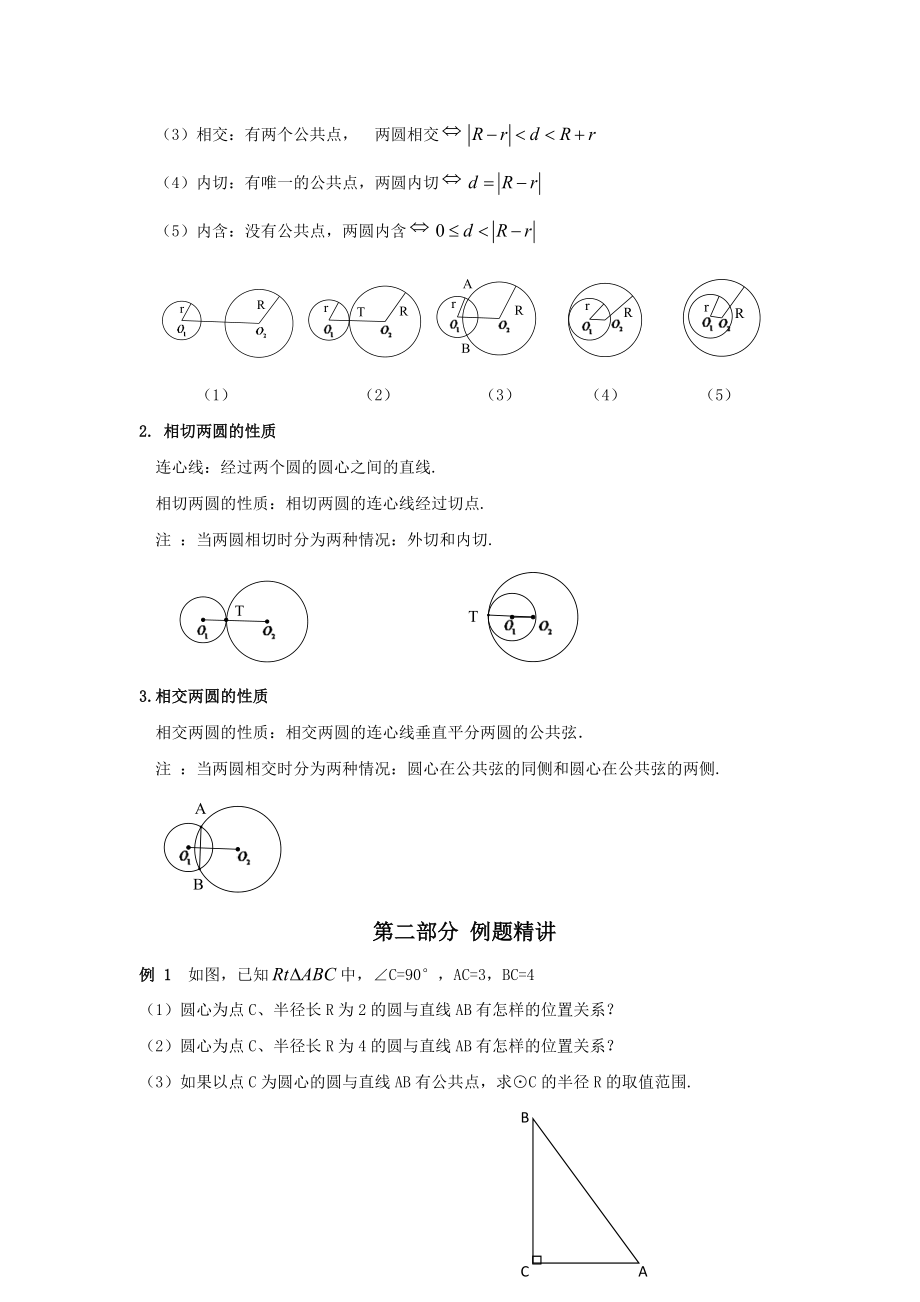
4、的切线”,简单地说,就是“联半径,证垂直”.二. 圆与圆的位置关系1. 圆与圆的五种位置关系在同一个平面内,两个不等的圆的位置关系共有五种:外离、外切、相交、内切、内含.圆心距:两圆圆心的距离叫做圆心距.设两圆的圆心距为,半径为,则有:(1)外离:没有公共点 ,两圆外离 (2)外切:有唯一的公共点,两圆外切(3)相交:有两个公共点, 两圆相交(4)内切:有唯一的公共点,两圆内切(5)内含:没有公共点,两圆内含 (1) (2) (3) (4) (5)2. 相切两圆的性质连心线:经过两个圆的圆心之间的直线.相切两圆的性质:相切两圆的连心线经过切点.注 :当两圆相切时分为两种情况:外切和内切. 3.
5、相交两圆的性质相交两圆的性质:相交两圆的连心线垂直平分两圆的公共弦注 :当两圆相交时分为两种情况:圆心在公共弦的同侧和圆心在公共弦的两侧. 第二部分 例题精讲例 1 如图,已知中,C=90°,AC=3,BC=4(1)圆心为点C、半径长R为2的圆与直线AB有怎样的位置关系?(2)圆心为点C、半径长R为4的圆与直线AB有怎样的位置关系?(3)如果以点C为圆心的圆与直线AB有公共点,求C的半径R的取值范围.ABC出题意图:考查直线与圆的位置关系.解析:利用圆心到直线的距离与半径比较即可得出圆与直线的位置关系.答案: 解:在中,C=90°,AC=3,BC=4.由勾股定理,得AB=5
6、.设点C到AB的距离为d,则 即 解得 d=2.4.(1)2.42,即dR 半径长R为2的C与直线AB相离.(2)2.44,即dR,半径长R为4的C与直线AB相交.(3)如果以点C为圆心的圆与直线AB有公共点,那么C与直线AB相切或相交.当R2.4时,C与直线AB有公共点.针对训练 1已知中,ABC=90°,AB=3,BC=4,以B为圆心作B.(1)若B与斜边AC只有唯一一个公共点,求B的半径长R的取值范围.ACB(2)若B与斜边AC没有公共点,求B的半径长R的取值范围.例 2 已知:直线AB经过O上的点C,并且OA=OB,CACB求证:直线AB是O的切线出题意图:考查切线的判定定理
7、.解析:欲证AB是O的切线,由于AB过圆上点C,若连结OC,则AB过半径OC的外端,只需证明OCAB即可.答案:证明:连结0C0A0B,CACB0C是等腰三角形0AB底边AB上的中线ABOC 直线AB经过半径0C的外端C,并且垂直于半径0CAB是O的切线针对训练 2如图,AC是O的弦,AC=BC=OC.求证:AB是O的切线.ACB例3 如图,已知A、B、C两两外切,且AB=3厘米,BC=5厘米,AC=6厘米,求这个三个圆的半径长.出题意图: 考查圆与圆的位置关系.解析:利用外切两圆的圆心距等于半径之和即可.答案:解:设A、B、C的半径长分别为x厘米、y厘米、z厘米.A、B、C两两外切,AB x
8、y,BCyz,CAzx.根据题意,得关于x、y、z的方程组 解得A、B、C的半径长分别为2厘米、1厘米、4厘米.针对训练 3如图,O的半径为5厘米,点P是O外一点,OP=8厘米.求:(1)以P为圆心作P与O外切,小圆P的半径是多少?(2)以P为圆心作P与O内切,大圆P的半径是多少? 例4 相交两圆的公共弦长为6,若两圆半径分别为8和5,求两圆的圆心距.出题意图: 考查相交两圆的性质.解析:两圆相交要考虑两种情况:(1)圆心在公共弦的同侧,此时圆心距等于两条弦心距之和;(2)圆心在公共弦的两侧,此时圆心距等于两条弦心距之差的绝对值.答案: 解:圆心在公共弦的两侧 为AB的垂直平分线AB,AC=C
9、B圆心在公共弦的同侧由可得:,针对训练 4已知和相交于A、B两点,P是连心线与的交点,PA、PB的延长线分别交于点C、D.求证:例5 如图,与内切于点P,经过上点Q的切线与相交于A、B两点,直线PQ交于点R.求证:出题意图: 考查相切两圆的性质.解析: 利用相切两圆的性质:两圆相切,连心线过切点.本题中过两个圆心作一条直线,则这条之间直线必过点P,然后利用圆中的相关知识即可解答.答案: 证明:联结、,作直线. 与内切于点P经过点P,与相切与点Q.针对训练 5如图,与外切于点P,经过上点Q的切线与相交于A、B两点,直线PQ交于点R.求证:例6 在中,点、在BC上,、外切于点P. 与AB相切于点D
10、,与AC相离;与AC相切于点E,与AB相离.(1)求证:DPAC.(2)设的半径长为x,的半径长为y,求y与x之间的函数解析式,并写出定义域.出题意图:考查圆与圆位置关系的综合应用解析: 利用等腰三角形的性质和圆与圆的位置关系,可推导出第一问的结论,再结合锐角三角比的知识推出函数解析式,在考虑定义域的时候要考虑到相关动点的临界位置问题,这是个难点,需要多加注意.答案: 解:(1)联结与AB相切于点D (2)联结,则,作于H.同理当与重合时,与相切,此时当与重合时,与相切,此时针对训练 6在中,圆A的半径长为1,若点O在BC边上运动(与点B、C不重合),设BO=x,的面积为y.(1)求y关于x的
11、函数解析式,并写出函数的定义域.(2)以点O为圆心、BO为半径作圆O,求当圆O与圆A相切时,的面积.第三部分 优化作业基础训练题(A)1. 下列直线中,不能判定为圆的切线的是 ( )A.与圆仅有一个公共点的直线;B.与圆心的距离等于半径长的直线;C.过半径的端点且与该半径垂直的直线;D.过直径的端点且与该直径垂直的直线.2. 已知的直径等于12cm,圆心O到直线的距离为5cm,则直线与的交点个数为( )A. 0 B. 1 C. 2 D.无法确定3. 的半径为3厘米,的半径为2厘米,圆心距=5厘米,这两圆的位置关系是( )A.内含 B.内切 C.相交 D.外切4.已知两圆的直径分别为6cm和10
12、cm,当两圆外切时,它们的圆心距d的大小是( )A. B. C. D. 5.已知线段AB=3cm,的半径为4cm,若与相切,则的半径为 cm.6.如图,AB与相切于点C,OA=OB,若的直径为8cm,AB=10cm,那么OA的长是 cm.7.设的半径为r,圆心O到直线a的距离为d,若d=r,则直线a与的位置关系是 .8.两圆的直径分别为3+r和3-r,若它们的圆心距为r,则两圆的位置关系为 .9.已知、的半径长分别是3cm、5cm,如果与内含,那么圆心距d的取值范围为 .10.两圆的半径之比为5:3,如果当它们外切时,圆心距长为16,那么当它们内切时,圆心距长为 .11.已知和的半径为方程的两
13、个根,若,试判断和的位置关系.12.如图,在直角梯形ABCD中,ADBC,CDAD,AD+BC=AB.求证:以AB为直径的 与CD相切.13.如图,OA=OB=8,OAOB,以O为圆心、OA为半径作,与以OA为直径的相切于点E,与相切于F,与OB相切于D,求的半径长. 14.如图,已知A是、的一个交点,点P是的中点.过点A的直线MN垂直于PA,交、于M、N.求证:AM=AN.15.已知和相交于A、B两点,公共弦与连心线相交于点G,若AB=48,的半径,的半径.求的面积.提高训练题(B)1. 已知的半径为2,直线上有一点P满足PO=2,则直线与的位置关系是( )A.相切 B.相离 C. 相离或相
14、切 D.相切或相交2. 已知 三边分别是,两圆的半径,圆心距,则这两个圆的位置关系是( )A.相交 B.内切 C.外切 D.内含3.两圆的半径长度分别为R和r,两圆心间的距离为d,如果将长度分别为R、r、d三线段首尾相接可以围成一个三角形,则两圆的位置关系是 .4.两个半径都等于2cm的和的圆心距,则与这两个圆都相切,且半径为3cm的圆有 个.5.中,B=90°,A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心、DB为半径作圆D.(1)求证:AC是圆D的切线;(2)求证:AB+EB=AC. 6. 如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A
15、为圆心,AB为半径的圆弧外切,求tanEAB的值. 7. 如图,点在的直径的延长线上,点在上,.(1)求证:是的切线;(2)若的半径为3,求的长(结果保留) 8.如图,已知ABC中,C=90°,AC=12,BC=8,以AC为直径作,以B为圆心,4为半径作.求证:与相外切.9.如图,已知与交于B、C两点,A在上,AD是的直径,AD交BC于M,AE是的弦,AE交BC于N.若AM=4cm,AN =6cm,AE=24cm,求的半径. 10.如图,AB为半圆O的直径,P是AB延长线上一点,将线段PA绕点P旋转到与半圆O相切的位置PC,这时切点为E,AC与半圆相交于点D.(1)求证:;(2)若C
16、D=2AD,求CE:EP 的值;(3)若E是PC的中点,求AD:DC的值.综合迁移题(C) 1. 如图,矩形ABCD中,AD=a,AB=b,(a>b),以C为圆心,CD的长为半径作圆弧交BC于E,以B为圆心、BE长为半径作圆弧交AB于F,以A为圆心、AF为半径作圆弧恰与弧DE相切.求的值.2. 已知,如图所示,圆O1与圆O2相交于A、B两点,过A点的弦分别交两圆于C、D,弦CE/DB,连结EB,试判断EB与圆O2的位置关系,并证明你的结论.3.在中,AC=3,AB=4,O是BC上的一点,以O为圆心,OC为半径作圆交AC于点D,交BC于点,过作的切线交AB边于点E,连BD,设OC=x,的面
17、积为y.求y与x之间的函数关系式.4. 在直角坐标平面内,为原点,点的坐标为(1,0),点的坐标为(0,4),直线轴(如图7所示)点与点关于原点对称,直线(为常数)经过点,且与直线CM相交于点D,联结OD(1)求的值和点D的坐标;(2)设点P在轴的正半轴上,若POD是等腰三角形,求点的坐标;(3)在(2)的条件下,如果以PD为半径的与外切,求的半径CMOxy1234A1BD参考答案:针对训练1. (1) (2)2. 通过等边对等角和三角形的内角和定理可以推出OAB=90°即可得出答案.3.(1)P1的半径是3cm (2)P2的半径是13cm4. 利用相交两圆公共弦的定理以及同圆弦心距
18、相等则弦所对的劣弧相等即可得出答案.5. 利用两圆相切连心线过切点的定理即可解答.6.(1) (2)(提示:第二问要考虑圆A和圆O外切、内切两种情况)基础训练题(A)1. C2. C 3. D4. A5. 1cm或7cm6. 7. 相切8. 内切9. 10. 411. 两圆内含.(提示:算出半径之和和半径之差的绝对值,然后与圆心距比较即可)12. 证明略.(提示:过点O做OECD于点E,证得OE等于圆的半径OA即可)13. 半径长为2.(提示:联结各个圆心距,利用相切两圆的性质和勾股定理即可)14. 证明过程略.(提示:过两个圆心分别向MN作垂线,再利用圆中的知识即可)15. 600或168.(提示:分圆心在公共弦的同侧和圆心在公共弦的两侧两种情况)提高训练题(B)1. D 2. A 3. 相交4. 45.证明过程略(提示:(1)向AC作垂线,用圆心到直线的距离等于半径来判定直线与圆相切.(2)通过证三角形全等,将边转化,从而可以得出结论.)6. =7. (1)证明略(2)8. 证明过程略(提示:联
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 2025年中信房地产销售面试题库及答案
- 2025年牛剑申请笔试真题及答案
- 2025年万达房地产行业面试题库及答案
- 2025年文学社区工作面试题库及答案
- 2025年中学教资体育笔试题及答案
- 2025年工程造价公开招聘笔试题及答案
- 2024年金湖县招教考试备考题库附答案解析(必刷)
- 2025年华东师范大学马克思主义基本原理概论期末考试模拟题附答案解析
- 2026年信阳艺术职业学院单招职业适应性考试模拟测试卷带答案解析
- 2025年内蒙古机电职业技术学院马克思主义基本原理概论期末考试模拟题含答案解析(必刷)
- 2026贵州贵阳市安航机械制造有限公司招聘8人考试重点试题及答案解析
- 2026年空天科技卫星互联网应用报告及未来五至十年全球通信创新报告
- (正式版)DB51∕T 3342-2025 《炉灶用合成液体燃料经营管理规范》
- 2025年上海市普通高中学业水平等级性考试地理试卷(含答案)
- 腔镜器械的清洗与管理
- 江南大学《食品科学与工程》考研真题及答案解析
- 眼科:青光眼患者药物治疗指南
- 2025年计算机等级考试(NCRE)一级人工智能与大模型基础样题及参考答案
- 2025年汉语桥的考试题目及答案
- 医护服务意识培训
- 芬兰烟熏桑拿体验创新创业项目商业计划书

评论
0/150
提交评论