九年级数学相似三角形复习

1、 笃学 精博 严谨 创新 数学需要专心听讲、积极思考。数学也需要练习，练习的目的不是为了完成，是为了加强记忆，加强理解。而订正的目的是为了纠正错误，防止再次的情况发生。九年级数学上册（华东师大版）第3章 图形的相似1. 相似图形形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形. 2. 比例线段的相关概念 如果选用同一单位量得两条线段的长度分别为，那么就说这两条线段的比是，或写成注意：在求线段比时，线段单位要统一，单位不统一应先化成同一单位在四条线段中，如果的比等于的比，那么这四条线段叫做成比例线段，简称比例线段注意：(1)当两个比例式的每一项都对应相同，两个比例式才是同一比例式(

2、2)比例线段是有顺序的，如果说是的第四比例项，那么应得比例式为：3. 比例的性质（1） 比例的基本性质比例式化积、积化比例式.a:b=c:d 注意：由一个比例式只可化成一个等积式，而一个等积式共可化成八个比例式，如，除了可化为，还可化为，更比性质(交换比例的内项或外项)：(2)反比性质 (把比的前项、后项交换) (3)合、分比性质 分子加（减）分母,分母不变. (k=1、2、3)应用: 已知 证明: (4)等比性质:分子分母分别相加，比值不变. 若则注意：(1)此性质的证明运用了“设法” ，这种方法是有关比例计算，变形中一种常用方法(2)应用等比性质时，要考虑到分母是否为零(3)可利用分式性质

3、将连等式的每一个比的前项与后项同时乘以一个数，再利用等比性质也成立如：；其中(5)比例中项:若的比例中项.4.平行线分线段成比例定理 (1).平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比.例. 已知l1l2l3, A D l1 B E l2 C F l3可得(2).推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. A D E B C由DEBC可得：.此推论较原定理应用更加广泛,条件是平行.(3).推论的逆定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. (即利用比例式证平行线)(4).定

4、理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. 5.黄金分割把线段分成两条线段，且使是的比例中项，叫做把线段黄金分割，点叫做线段的黄金分割点，其中0.6186. 相似三角形的概念对应角相等，对应边成比例的三角形，叫做相似三角形相似用符号“”表示，读作“相似于” 相似三角形对应边的比叫做相似比(或相似系数)相似三角形对应角相等，对应边成比例注意：对应性：即两个三角形相似时，通常把表示对应顶点的字母写在对应位置上，这样写比较容易找到相似三角形的对应角和对应边顺序性：相似三角形的相似比是有顺序的两个三角形形状一样，但大小不一定一样全等三角形是相似比为1

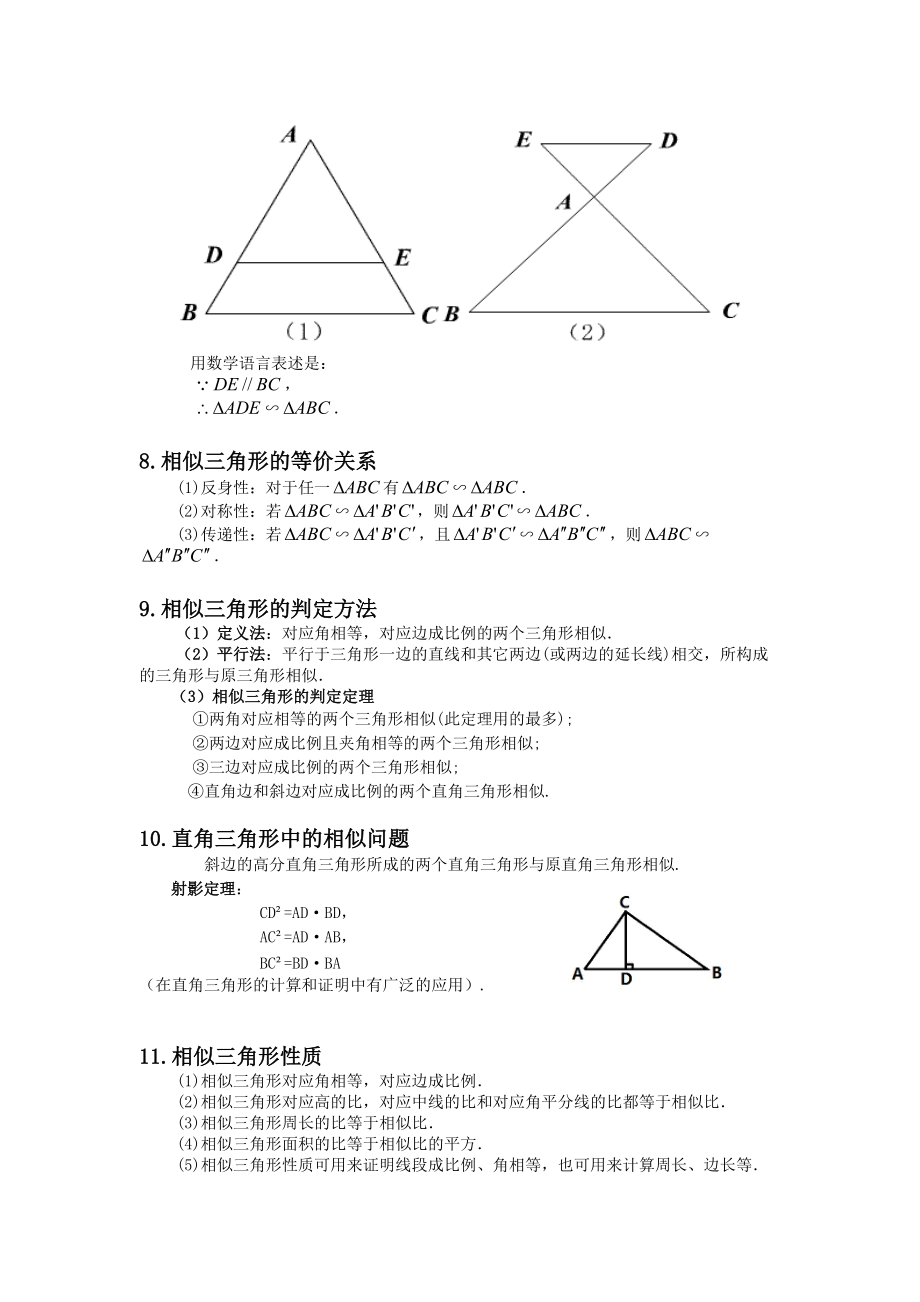
5、的相似三角形二者的区别在于全等要求对应边相等，而相似要求对应边成比例7. 相似三角形的基本定理定理：平行于三角形一边的直线和其它两边(或两边延长线)相交，所构成的三角形与原三角形相似定理的基本图形：用数学语言表述是：，8. 相似三角形的等价关系(1)反身性：对于任一有 (2)对称性：若，则 (3)传递性：若，且，则9. 相似三角形的判定方法（1）定义法：对应角相等，对应边成比例的两个三角形相似（2）平行法：平行于三角形一边的直线和其它两边(或两边的延长线)相交，所构成的三角形与原三角形相似（3）相似三角形的判定定理 两角对应相等的两个三角形相似(此定理用的最多); 两边对应成比例且夹角相等的两

6、个三角形相似; 三边对应成比例的两个三角形相似; 直角边和斜边对应成比例的两个直角三角形相似.10. 直角三角形中的相似问题斜边的高分直角三角形所成的两个直角三角形与原直角三角形相似.射影定理：CD²=AD·BD， AC²=AD·AB，BC²=BD·BA（在直角三角形的计算和证明中有广泛的应用）.11. 相似三角形性质(1)相似三角形对应角相等，对应边成比例(2)相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比(3)相似三角形周长的比等于相似比(4)相似三角形面积的比等于相似比的平方(5)相似三角形性质可用来证明线段成

7、比例、角相等，也可用来计算周长、边长等12. 相似多边形如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形相似多边形对应边的比叫做相似比(相似系数)13. 相似多边形的性质(1)相似多边形周长比，对应对角线的比等于相似比(2)相似多边形中对应三角形相似，相似比等于相似多边形的相似比(3)相似多边形面积比等于相似比的平方注意：相似多边形问题往往要转化成相似三角形问题去解决，因此，熟练掌握相似三角形知识是基础和关键14. 与位似图形有关的概念1. 如果两个图形不仅是相似图形，而且每组对应顶点的连线都交于一点，那么这样的两个图形叫做位似图形. 2. 这个点叫做位似中心，这

8、时的相似比又称为位似比. 拓展： （1） 位似图形是相似图形的特例，位似图形不仅相似，而且对应顶点的连线相交于一点. （2） 位似图形一定是相似图形，但相似图形不一定是位似图形. （3） 位似图形的对应边互相平行或共线. 15. 位似图形的性质位似图形上任意一对对应点到位似中心的距离之比等于相似比. 拓展：位似图形有许多性质，它具有相似图形的所有性质.16. 画位似图形1. 画位似图形的一般步骤： （1） 确定位似中心 （2） 分别连接原图形中的关键点和位似中心，并延长（或截取）. （3） 根据已知的位似比，确定所画位似图形中关键点的位置. （4） 顺次连结上述得到的关键点，即可得到一个放大或

9、缩小的图形. 2. 位似中心的选取： （1） 位似中心可以在图形外部，此时位似中心在两个图形中间，或在两个图形之外. （2） 位似中心可取在多边形的一条边上. （3） 位似中心可取在多边形的某一顶点上. 说明：位似中心的选取决定了位似图形的位置，以上位似中心位置的选取中，每一种方法都能把一个图形放大或缩小.17. 相似三角形中的常见图形 （1）若DEBC（A型和X型）则ADEABC （2）射影定理 若CD为RtABC斜边上的高（双直角图形） 则RtABCRtACDRtCBD且AC2=AD·AB，CD2=AD·BD，BC2=BD·AB； （3）满足1、AC2=AD&

10、#183;AB，2、ACD=B，3、ACB=ADC，都可判定ADCACB（4）当或AD·AB=AC·AE时，ADEACB （3） （4）2、 典型例题解析：例1.如果xyz135，那么_例2.如图，有一块呈三角形形状的草坪，其中一边的长是20 m，在这个草坪的图纸上，这条边长5 cm，其他两边的长都是3.5 cm，求该草坪其他两边的实际长度.例3.已知线段d是线段a、b、c的第四比例项，其中a2 cm，b4 cm，c5 cm，则d等于（）（A）1 cm（B）10 cm（C） cm（D） cm例4如图，l1l2l3，BC3，2，则AB_例5.如图，在ABC中，AB15 cm，

11、AC12 cm，AD是BAC的外角平分线，DEAB交AC的延长线于点E，那么CE_cm 例6.如图，在ABC中，M、N是AB、BC的中点，AN、CM交于点O，那么MONAOC面积的比是_ 例7.如图，在正方形ABCD中，F是AD的中点，BF与AC交于点G，则BGC与四边形CGFD的面积之比是_例8.如图，点C、D在线段AB上，PCD是等边三角形（1）当AC、CD、DB满足怎样的关系时，ACPPDB？（2）当ACPPDB时，求APB的度数 例9.已知：如图，在正方形ABCD中，P是BC上的点，且BP3PC，Q是CD的中点求证：ADQQCP例10.已知：如图，ABC中，ABAC，AD是中线，P是A

12、D上一点，过C作CFAB，延长BP交AC于E，交CF于F求证：BP2PE·PF例11.如图，在梯形中，梯形的高为动点从点出发沿线段以每秒2个单位长度的速度向终点运动；动点同时从点出发沿线段以每秒1个单位长度的速度向终点运动设运动的时间为（秒）（1）当时，求的值；（2）试探究：为何值时，为直角三角形 例12.如图，在平面直角坐标系中，已知OA=12cm，OB=6cm，点P从O点开始沿OA边向点A以1cm/s的速度移动：点Q从点B开始沿BO边向点O以1cm/s的速度移动，如果P、Q同时出发，用t(s)表示移动的时间（），那么：（1）设POQ的面积为，求关于的函数解析式。（2）当POQ的面

13、积最大时， POQ沿直线PQ翻折后得到PCQ，试判断点C是否落在直线AB上，并说明理由。（3）当为何值时， POQ与AOB相似？例13.亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部，颖颖的头顶及亮亮的眼睛恰在一条直线上时，两人分别标定自己的位置，然后测出两人之间的距离，颖颖与楼之间的距离（，在一条直线上），颖颖的身高，亮亮蹲地观测时眼睛到地面的距离你能根据以上测量数据帮助他们求出住宅楼的高度吗？3 课堂实战演练1. 已知 ，则下列式子中正确的是（ ）A.a:b=

14、c²：d² B.a:d=c:d C.a:b=(a+c):(b+d) D.a:b=(a-d):(b-d)2. 一个运动场的实际面积是6400m²，那么它在比例尺1:1000的地图上的面积是（ ）² B.640cm² C.64cm² D.8cm²3. 测得线段AB=2.8m，CD=310cm，则线段AB与CD的比为（ ） 4. 已知线段d是线段b、c、a的第四比例项，其中a=5cm,b=2cm,c=4cm,则d等于（ ）5. 如果线段d是线段a、b、c的第四比例项，则有 ； 如果点C是线段AB的中点，那么AC是AB、BC的比例中

15、项； 如果点C是线段AB的黄金分割点，且AC>BC，那么AC是AB与BC的比例中项； 如果点C是线段AB的黄金分割点，且AC>BC，AB=2，则AC= .其中正确的判断有（ ）A.1个 B.2个 C.3个 D.4个6. 如图，DEBC,在下列比式中，不能成立的是（ ） 7. 下列图形中相似的多边形是（ ）A.所有的矩形 B.所有的菱形 C.所有的正方形 D.所有的等腰梯形8. 下列判断中，正确的是（ ）A.各有一个角时67°的两个等腰三角形相似； B.邻边之比都为2:1的两个等腰三角形相似； C.各有一个角时45°的两个等腰三角形相似；D.邻边之比都为2:3的两

16、个等腰三角形相似.9. 在RtABC中，CD是斜边AB上的高，则ABC中相似三角形共有（ ）A.1对 B.2对 C.3对 D.4对10. 点D、E分别是ABC的边AB、AC的中点，则SADE:SABC=（ ）A.1:2 B.1:3 C.1:4 D.1:211. ，则k=（ ） A.2 B.-1 C.2或-1 D.无法确定12. 下列说法正确的是（ ）A.两位似图形的面积比等于位似比；B.位似图形的周长之比等于位似比的平方；C.分别在ABC的边AB、AC的反向延长线上取点D、E，使DEBC，则ADE是ABC放大后的图形； A. B. C. D.D.位似多边形中对应对角线之比等于位似比13. 如果

17、一个直角三角形的两条直角边分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x，那么x的值（ ）A.只有1个 B.可以有2个 C.有2个以上，但有限 D.有无数个14. 如图，在ABC中，D为AC边上一点，DBC=A，BC=6，AC=3，则CD的长为( )A.1 B. C.2 D. 15. 如图，在RtABC中，C=90°，CDAB于D，且ADBD=9:4，则AC:BC的值为（ ）A.9:4 B. 9:2 C.3:4 D.3:2 二填空题16. _, _.17. 如果x:y:z=1:3:5,那么 _.18. E、F为线段AB的黄金分割点，已知AB=10cm，则EF的长度为_c

18、m.19. 在阳光下，身高1.68m的小强在地面上的影长为2m，在同一时刻，测得学校的旗在地面上的影长为18m.则旗杆的高度为_（精确到0.1m）.20. 两个相似三角形对应高的比为1:2,则它们的周长之比为_;面积之比为_.21. ABC的三边长分别为5、10、15， 的两边长分别为1和2，如果ABC ，那么 的第三边长为_.22. 如图，在平行四边形ABCD中，延长AB到E,使AB=2BE，延长CD到F，使DF=DC，EF交BC于G，交AD于H.则SBEG:SCFG=_.23. 如图，AB是斜靠在墙上的一个梯子，梯脚B距墙1.4m，梯墙一点D距强1.2m， BD长0.5m，则梯长为_. （

19、23题） (24题)24. 如图，在ABC中，BAC=90°，D是BC中点，AEAD交CB延长线于点E，则BAE相似于_. 25. 如图，在ABC中，M、N是AB、BC的中点， AN、CM交于点O，那么MOCAOC面积的比为_.一、 作图题（5分）26. 三角形的顶点坐标分别是A（2,2），B(4,2)，C(6,4)，试将ABC缩小，使缩小后的DEF与ABC的对应边比为1:2，并且直接写出点D、E、F的坐标.二、 解答题（27题、28题5分，29题10分，共20分）27. 如图，DEBC，DFAC，AD=4cm，BD=8cm，DE=5cm，求线段BF的长.28. 如图，已知ABC中，AE:EB=