《直线与平面平行的判定》教学设计1

1、直线与平面平行的判定教学设计教材：人教A版必修二执教人：刘战献学校：安顺二中2019年6月10日“直线与平面平行的判定”教学设计授课教师：刘战献 学校：安顺二中一、教学目标与要求1. 知识与技能：理解并掌握直线与平面平行的判定定理；能应用定理证明简单的线面平行问题.2. 过程与方法：通过直感知-操作确认-思辨论证的认识方法，经历直线与平面平行的判定定理的发现过程，培养学生合情推理能力，进一步渗透化归和转化的数学思想，渗透立体几何将空间问题降维为平面问题的一般方法. 初步掌握立体几何中的三种语言的应用，并培养学生的观察、探究、发现能力和空间想象能力、逻辑思维能力.3. 情感态度与价值观：通过数学

2、思辨和推理过程培养学生说理、批判、质疑的严谨风格和理性精神；领会数学科学的应用价值，激发学生的数学学习兴趣，培养学生主动探究,主动提出问题的习惯.二、教学重点与难点（一）教学重点：直线与平面平行的判定定理的理解与简单应用.（二）教学难点：线面平行判定的应用，平行辅助线的作法三、教学过程 教学阶段教学设计设计意图复习回顾直观感知提出问题【必备知识】（1）直线与平面的位置关系有_、_、_三种.（2）直线与平面平行的定义：直线与平面_公共点【直观感知】（1）让学生观察门转动到离开门框的任何位置时，门的边缘线始终与门框所在的平面平行（由教师用模型展示）（2）让学生观察书本的形状，得出两条对边所在直线平

3、行。接着让学生翻开书的封面观察封面边缘所在直线与书面所在平面的位置关系，通过观察得出，它们平行。抽象出实验中的两条直线与一个平面，做出对应的图形。将生活中的实物抽象成数学图形.抽象：如何判定线面平行？复习回顾线面关系及线面平行的定义，为后面的学习做好铺垫将生活中的实物抽象为几何图形，直观感知线面位置关系.通过设置情境进一步让学生体会线面位置关系普遍存在在我们的生活中；通过实际问题的提出，引发学生的认知冲突，激发学生的学习兴趣，使判定定理的引入更加迫切与自然.让学生完整体会数学概念和问题的抽象与提炼过程.探究说理操作确认【自主探究】探究：动手操作：设纸张的一边AB所在直线为直线a，如图，将纸张进

4、行翻折，设底面为，折痕CD所在直线为直线b问题1：怎样翻折才能使得直线a与底面平行？问题2：当a/b时，转动四边形ABCD，转动过程中，直线a与平面的位置关系是怎样的？定理的发现采用“直观感知实验探究操作确认归纳提炼”的过程，让学生清楚的看到线面平行的关键因素是什么，让学生在自主探究和合作中，通过问题的引导思维逐步深入.教材并没有要求证明判定定理，但考虑到欧式几何的公理化体系，数学的严密性，这里采用说理的形式，让学生深刻理解定理.归纳提炼得出定理问题3：根据以上分析，你觉得使直线a/的关键因素有哪些？（平面外一条线 平面内一条直线 这两条直线平行）问题4：你能用三种语言描述我们得到的成果吗？线

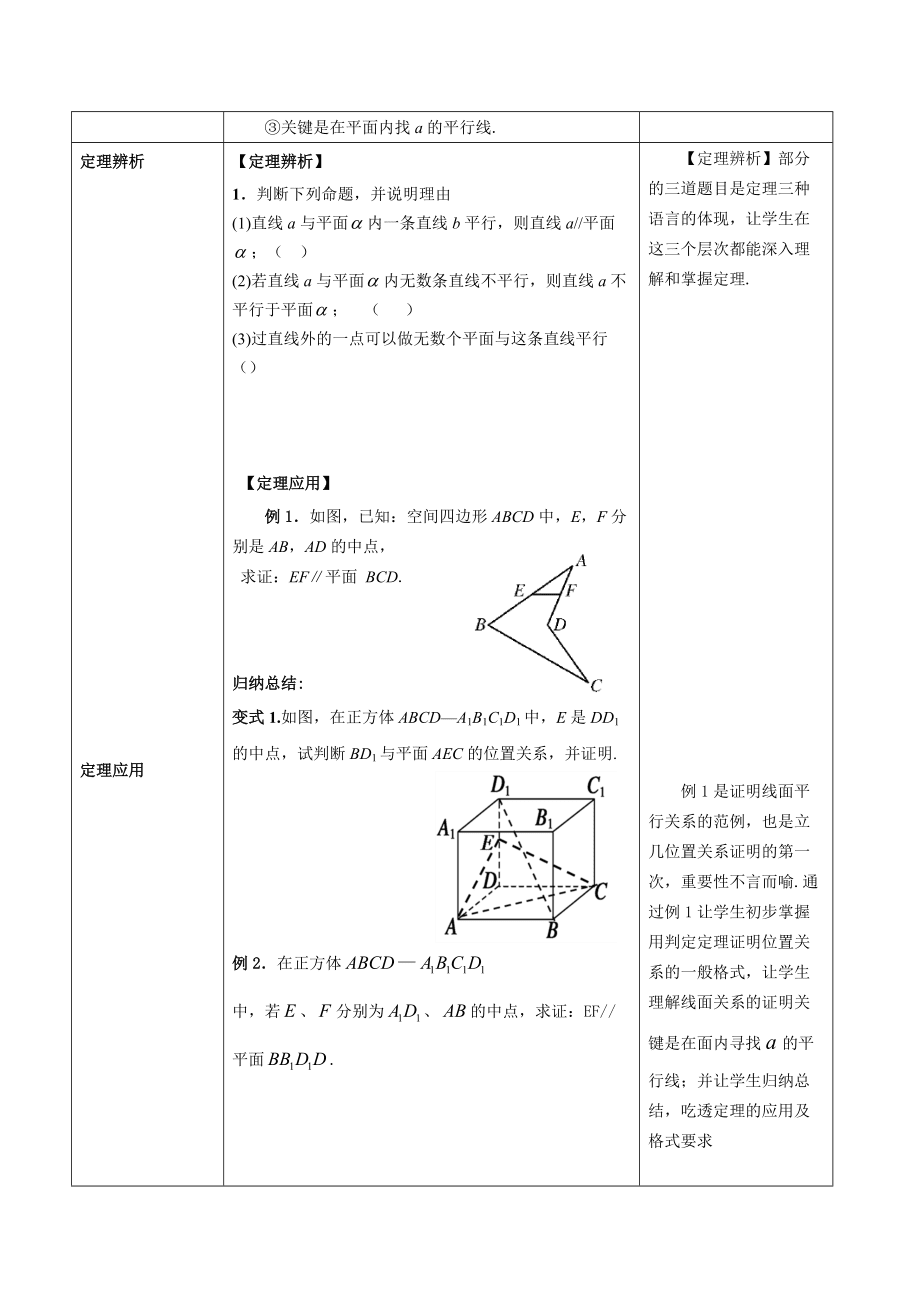
5、面平行的判定定理：平面外一条直线与此平面被一条直线平行，则该直线与此平面平行.符号语言：图形语言：注：内外两线平行，则线面平行； 线线平行线面平行（空间问题平面化）； 关键是在平面内找a的平行线.通过问题3，培养学生的抽象概括能力，逐步形成从探究活动中提炼数学原理与模型的能力.考虑到学生刚刚接触线面位置关系，设计问题4，让学生明白三种语言在立几研究中的重要性，并为后面严密的数学推理与证明打下基础.定理辨析定理应用【定理辨析】1判断下列命题，并说明理由(1)直线a与平面内一条直线b平行，则直线a/平面；（ ）(2)若直线a与平面内无数条直线不平行，则直线a不平行于平面； （ ）(3)过直线外的一

6、点可以做无数个平面与这条直线平行（） 【定理应用】例1如图，已知：空间四边形ABCD中，E，F分别是AB，AD的中点，求证：EF平面 BCD.归纳总结:变式1.如图，在正方体ABCDA1B1C1D1中，E是DD1的中点，试判断BD1与平面AEC的位置关系，并证明.例2在正方体 中，若、分别为、的中点，求证：EF/平面.变式2. 如图，四棱锥中，为线段上一点，为的中点证明：平面；【定理辨析】部分的三道题目是定理三种语言的体现，让学生在这三个层次都能深入理解和掌握定理.例1是证明线面平行关系的范例，也是立几位置关系证明的第一次，重要性不言而喻.通过例1让学生初步掌握用判定定理证明位置关系的一般格式，让学生理解线面关系的证明关键是在面内寻找a的平行线；并让学生归纳总结，吃透定理的应用及格式要求例2主要强调平行四边形及平行传递性在寻找平行直线时的应用；变式2是一道探究性题目，目的在于提高让学生对辅助线的做法的认识.总结归纳总结提问：（1）这节课我们学习了哪些知识点以及方法？（2）在学习的过程中，我们应用了哪些数学思想？学生发言，互