中考反比例函数分类汇编及答案

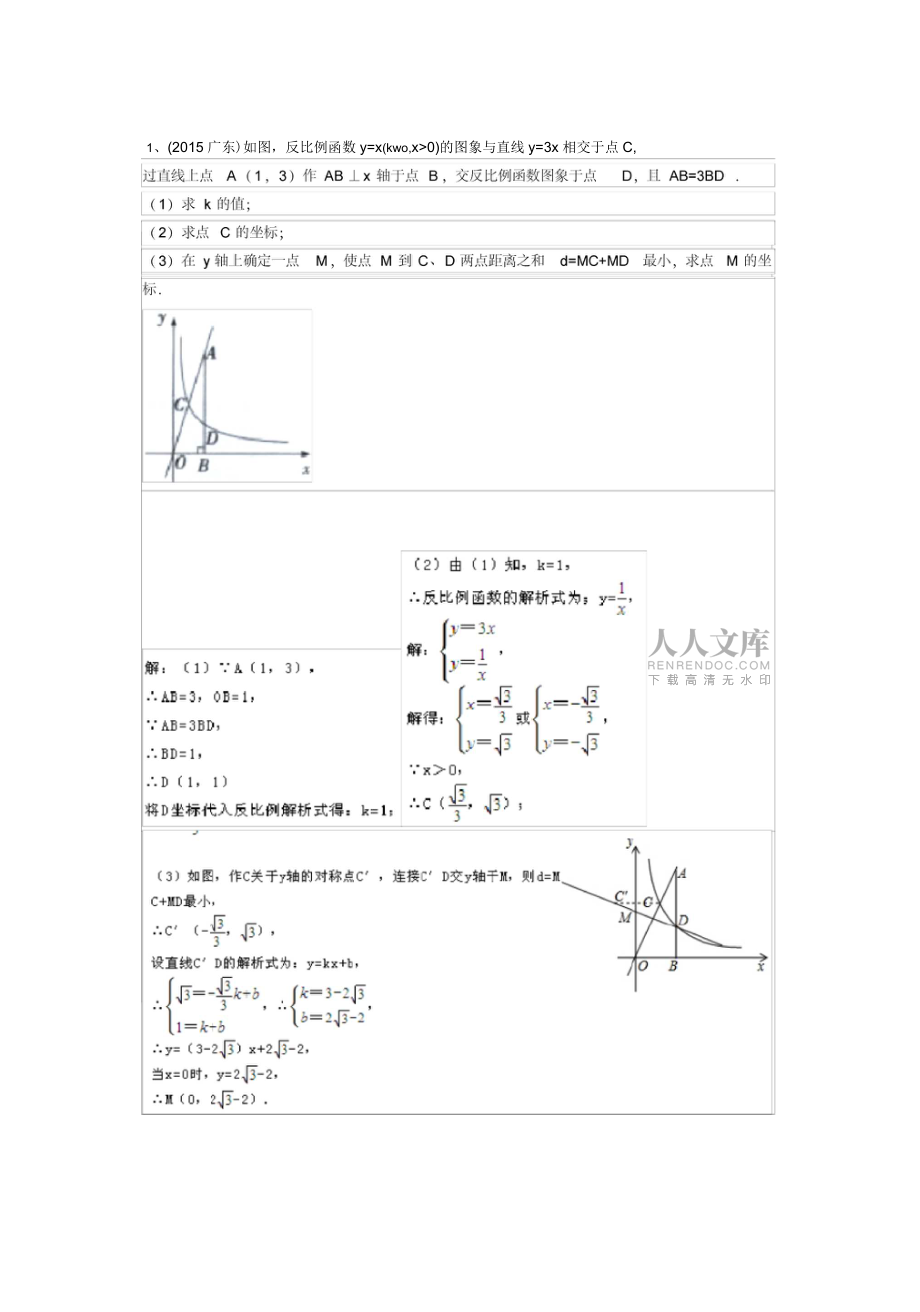
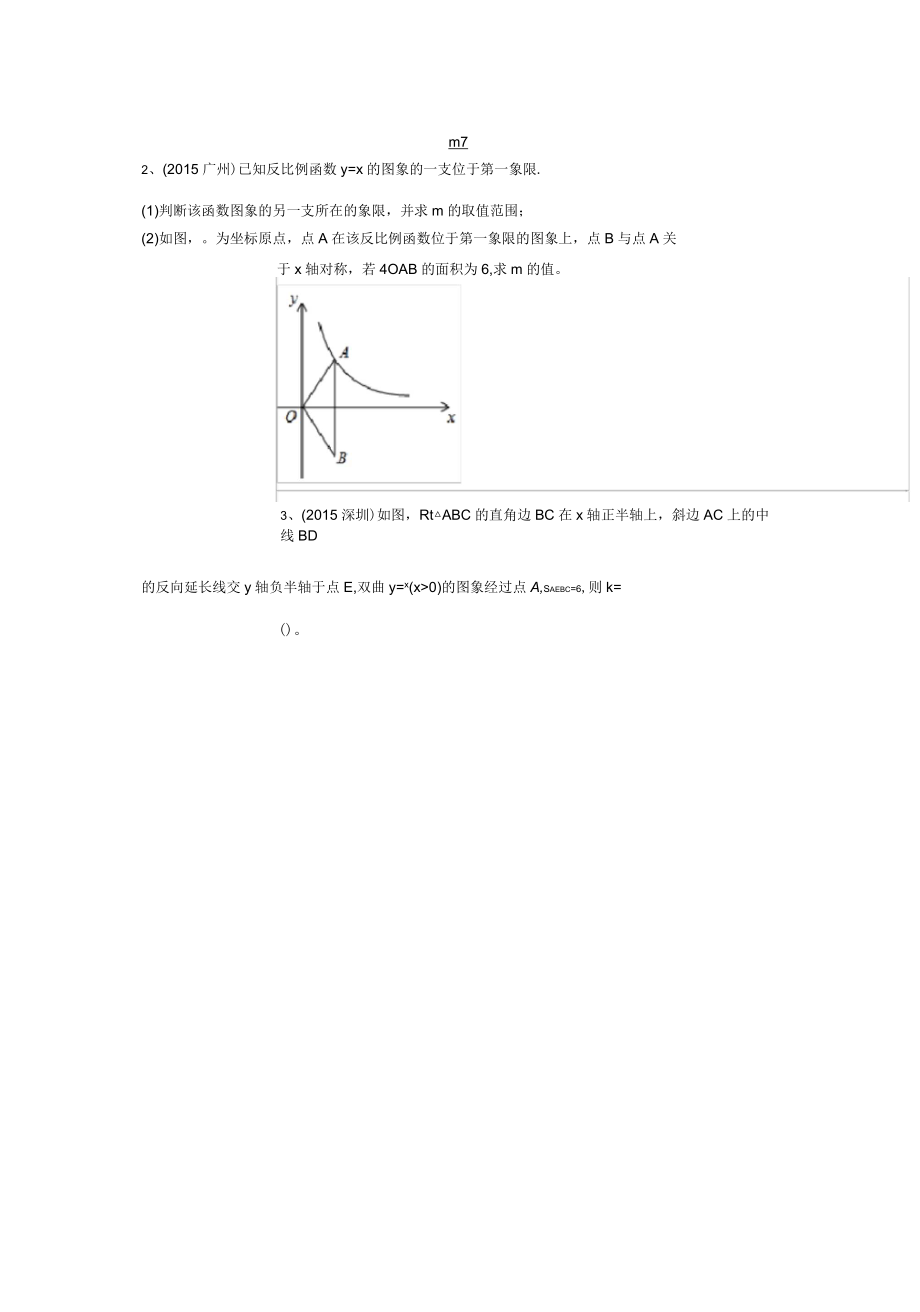
1、2015年中考反比例函数分类汇编及答案1、(2015广东)如图，反比例函数y=x(kwo,x>0)的图象与直线y=3x相交于点C,m72、(2015广州)已知反比例函数y=x的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限，并求m的取值范围；(2)如图，。为坐标原点，点A在该反比例函数位于第一象限的图象上，点B与点A关于x轴对称，若4OAB的面积为6,求m的值。3、(2015深圳)如图，RtABC的直角边BC在x轴正半轴上，斜边AC上的中线BD的反向延长线交y轴负半轴于点E,双曲y=x(x>0)的图象经过点A,Saebc=6,则k=()。解；:ED为RtdAEC的斜

2、边AC上的中缥BD=DC*ZDEC=ZACB-又'/ZDBC=ZEBO,又TNEO邑三/，ABOEsACEh即BCE二RO%也X'-'SA=EC=SfOE=12=BO|11.又反比例函数图薮在第一端眼，k>U.二k等于12.4、22015珠海)如图，在平面直角坐标系中，矩形OABC的顶点A,C分别在x轴，yk轴上，函数y=x的图象过点p(4,3)和矩形的顶点B(m,n)(0vmv4).(1)求k的值；(2)连接PA,PB,若4ABP的面积为6,求直线BP的解析式解；(1)；函数尸£的图象过点P14，3J：.h=4x3=12si>2二函数广三的图象过

3、点B1上立)，xJmn=12.；AAEP的面积为6,P%3)(U<m<4,./n(4-m)=6*4n-12=L2-解得n_=6r.'.irt=2，点B(2,0).设直线BP的解析式为产皿十b,VB(2,6),P(4,3),.-.直线BP的解析式知产他b=X1X2,试判断a,b的大小关系，并说明理由.6、（2015茂名）在平面直角坐标系中，我们不妨把纵坐标是横坐标的2倍的点称之为理想点”，例如点（-2,-4）,（1,2）,（3,6）都是理想点”，显然这样的理想点”有有无数多个.k（1）若点M（2,a）是反比例函数y=x（k为常数，kO）图象上的理想点”，求这个反比例函数的表达

4、式；（2）函数y=3mx-1（m为常数，廿0）的图象上存在理想点”吗？若存在，请求出理想点”的坐标；若不存在，请说明理由.解二丫点皿（3a）是反比例函数广三八为常数，kHQ）图舞上的F理想点'点N2,4）在反比例函数产士为常蚊，图象上，X.,-lc=2X4=B）二反比例函数的解析式为工C2J微设函数学三3m-1轨为常数，加二口）的图象上存在“理想点”（戈，2票），则有31nleT二2k,整理得；K=l,2 1当3皿-2壬0，即皿壬二时，解得：.=一-一，3 3-2当3m2二口.即IIL二$3上无解，综上所述，当mH：时，函数图象上存在“理想点“，为亍I33加一23腕-2当m二当时，函数

5、图猿上不存在“理想点”.8（2015北京）在平面直角坐标系xOy中，直线y=kx+b（kwo）与双曲线y=x的一个交点A. B.P(2.m(1)求m的值;(2)若PA=2AB ,求k的值.2m=8 .解得二Jh=4;(2)点F (3 4)在产kK+b上./-4=2k+b(/ b-4- 2k ?丫直绷y=k算+b (k*0)局3c轴、y轴分即1交于点A, Bi.'.A2-丁，3) , B (Ot 4-2k)，如图，点A在x轴正半轴点b在y轴半釉时,VFA=2AB)解得* k=3.m(1)这个反比例函数的解析式;(2)直线AB的表达式个反比例函数的图象上，过点B作BC /x轴，交y轴于点C

6、,且AC=AB .求:4 x7、(2015上海)已知：如图，在平面直角坐标系xOy中，正比例函数 y= 3 的图象经过点A,点A的纵坐标为4,反比例函数y= x的图象也经过点 A ,第一象限内的点 B在这/. AB=PE,则 OARC，,r2=2,解得k二h当点且在*轴正半轴，点B在y轴负半轴时, 必1解正比例函数ym的图戴姐过点却点泄纵坐标为明，点A的坐标为（3-4）,.悯函数Y的图麴蜻过点A,，反比例函数的解析式为:12）加图，连接AC，AB,12产一Ix作AD_LBC手九VAC=AB1ADIBCp，6C=2CD=&，点B的坐林如:设直线AB的表达式为上y=kx+b-6kT=2工Q

7、=6，直殊AB的表达式为：7=-刁+6.（2015?重庆）如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A,B两点的纵坐标分别为3,1.反比例函数y=x的图象经过A,B两点，则菱A.2B.4C.D.解；过点A作曷由的孔线，与CE的延长线交干点E,，,加B两点在反比例函数好之的图霰上且细坐标分别为31,XH横坐标分别为13,，AE=2，EE=2，且B=2，号菱形*底乂高=2M2=4p，k110、(2015安徽)如图，已知反比例函数y=x与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).(1)求ki、k2、b的值；(2)求AOB的面积；ki(3)若M(%,y

8、j、N(X2,v。是反比例函数y=x图象上的两点，且Xi<X2,指出点M、N各位于哪个象限，并简要说明理由。11、(2015山西)如图，在平面直角坐标系xOy中，一次函数y=3x+2k的图象与y轴交于点A,与反比例函数y=x(kwo)在第一象限内的图象交于点B,且点kB的横坐标为1.过点A作AC±y轴交反比例函数y=x(kO)的图象于点C,连接BC.(1)求反比例函数的表达式.(2)求4ABC的面积.解：1）丫一次函数方坂十之的图象过点且点B的横坐标为I,，y=3x1+2=5!，点E的坐标为1,51.7点E在反比可函效的图领上，X,k=lXH=5,，反比例函数的表达式为产1（2

9、） ;一次函歆尸3/2的量藕与娟由交干点从，当x二口时，y=2），点A的坐标为tO,20*ACly轴，点C的纵坐标与点9的纵坐标相同，是3，,点C在反比例函触严三的图氯上,X,，当*2时，2=二解得次="x2.1.ac4过&作ED_LAC干DjJil3D=yB_yc=6-2=311 1515SA五二=；山亡ED=：X彳线3=-.2 22。k12、（2015江西）如图，已知直线y=ax+b与双曲线y=x（x>0）交于A（Xi,yj,B（X2,V2）两点（A与B不重合），直线AB与x轴交于P（X0,0）,与y轴交于点C.（1）若A,B两点坐标分别为（1,3）,（3,y2）,

10、求点P的坐标.（2）若b=yi+l,点P的坐标为（6,0）,且AB=BP，求A,B两点的坐标.（3）结合（1）,（2）中的结果，猜想并用等式表示xi,x2,x0之间的关系（不要求证明）4-6=33a-5= 1解：（1）直线y=ax+b与双曲线y=三（x>0）交手A（1,3）,/.k=IX3=3,.3y=-»XVB(3,yz)在反比例函数的图短上,.31yz=j=1，(3,1),:直线y=ax+b经过A、B两点,2=-l解得.0=4-直线为y=-x+4,令y=0,则x=4,AP(4,0);(2)如图，作ADJ.y轴干D,蛇上乂轴干五，86人丫轴千6,AE、BG交千H,贝4AD&q

11、uot;BGx轴，AEBFy轴，.CDADPF_BF.PB,=,9'一=二,1，OCOPPEAEPAVb=y-4-1.AB=BP.1_XIjl+1一丁PFJF.lPEAE2B(卓，*)M2TA,B两点都是反比例函数图嵌上的点，.6Tl1xryi=-eyy>解得yi=2,代人T=三,解得x=2,J1-16AA(2,2),B(4,1).（3）根据（1）j（2）中的结臬，猬想：xfX）之间的关系为x+xz=x3.k13、（2015成都）如图，一次函数y=-x+4的图象与反比例函数y=x（k为常数，且kwo）的图象交于A（1,a）,B两点.（1）求反比例函数的表达式及点B的坐标；（2）在

12、x轴上找一点P,使PA+PB的值最小，求满足条件的点P的坐标及4PAB的面积。解:11）把点A11.4代人-次函数产="明”得i明解得a=3V.'.A（1,3），点A3）代入反比例函域y="得入，二反比例函数的表达式了=±,°（y=-x-4D=3，解得工-二1，xz=3f，点6坐标（3，1）f（2）作点B作美干工轴的对秫点“交乂轴干点C,连接且D,交五轴干点P,此时PA+PE的值最小,D（3（-1）-设直线AD的解析式为y=mc+m,"1一！?=3把A,D两点代人得.，、3泪=库=-1解得m=-2,n=5»直裁AD的解析式为丁

13、=-2k此，令y=3将靠三三，点F坐标弓0）,SiFA&=SAA&；-SiF3C=TX2X2-1X2X1=2-一工上/上（1）根据图象直接回答：在第二象限内，当x取何值时，yi-y2>0?k14、（ 2015?兰州）在同一直角坐标系中，一次函数y=kx-k与反比例函数 y= x （kw。）的图象大致是（）k1 5、（ 2015?兰州）如图，点P、Q是反比例函数y= x图象上的两点，PA，y轴于点A,QN，x轴于点N,作PM，x轴于点M, QB，y轴于点B,连接PB、QM , AABP的面积记为Si, AQMN的面积记为S2,则Si =S2.（填 4”或N"或&q

14、uot;=）1),16、 （ 2015?兰州）如图，A （-4, 2B （-1, 2）是一次函数 y1=ax+b与反比例函数my2= x图象的两个交点， AC，x轴于点C,BD±y轴于点D.解3 iSp C St b） ? Q （hlf n）,则 S:包F b门口N 二一 £S A 之=（mi a.） n=1nL 仇一二以拄，；点FQ在反比例函数的图象上，(2)求一次函数解析式及m的值；(3)P是线段AB上一点，连接PC,PD,若4PCA和PDB面积相等，求点P的坐标。c%解：(1)y-y:>Oi即！>yz*，一次函数y=m的图象在反比例函题了落注图象的上面,X

15、,：A(-4,-J,B-，2)，当“GO1时.y-72>(i3(2) )了工二更图象过EJ1,2),Xm=-1X2-2,Vy=4X+bltAt-4,i),BC-L2),，一次函效解析式为qy=1s+(3)设PCm,1贰二)，过P作服_戈争由于M,PM_Ly亨由于H,二FH二1m+j?n=-m,Jdn4:/iPCAfi口£面相相等，(?<?”=/A闲解簿JL=-不二F<4，17、1)解：过乩作出1m轴干C,过E作BDlx轴干回k18、(2015?黄冈)如图，反比例函数y=x的图象经过点a(-1,4),直线y=-x+b(bw。)k(1)求k的值;交于点A,B,且A为OB

16、的中点，若函数y产x,则y2与x的函数表达式是(与双曲线y=x在第二、四象限分别相交于P,Q两点，与x轴、y轴分别相交于C,D两OC-i,AC-：AC_L土柏，轴,Ak=2aB=4?a，力与m的函数表达式是；y;=-Hx:点乩在反比例函数歹一上,XA(3().:O/iCsAOBD,.ac_oc_oa'瑟ODOBr为。B的中点，.AC_OC_OA_jD-0D0S=2r?.BD=2AC=,0D=2OC=2a,a故答案为：(2015?南京)如图，过原点O的直线与反比例函数y1,y2的图象在第一象限内分别(2)当b=-2时，求OCD的面积;b,使得Saodq=Saocd?若存在，请求出b的值；

17、若不存在,解：(1);反比例函数尸三的图默经过点内1-1,4).X/k=-l*4=_%(2)当b=-2时，直线解析式为y=-X-3Vy=OBt，-x-2=0,解雾豆=-2,C(-2,0),"，"当k=。时1J.D(0,-2),(3)存在.当行口时，-x+b-0,解得豆=b,则匚b,0D,"SA0DC=Si0CC5，点Q和点C到OD的距离相等*而Q点在第四象限，Q的横坐标为-当nu-bB寸，y=-x+b=2bt则QOb,2b),丁点Q在反比例函数4-土的图尊上，Xb'2b二一%解得b=-网b二舍去)，b的值为-JSm19、(2015襄阳)如图，已知反比例函数

18、y=x的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).(1)求反比例函数和一次函数的解析式；(2)当一次函数的值小于反比例函数的值时，直接写出x的取值范围I解：(i):反比例函数产里的图辣过点a(】，4)工4r即11=4,二反比例函里的解析式为：第二士不反比例函数产士的图象过点BCm,-2)，XJ.-2=±,n解得:口二-2AB1-3-21.二一次函数ysHbfkk。)的图象过点A(1，4J和点B(-2,-2).一次国教的解析式为：*29备(2)由图象可知:当芯<-2或口Mx<l时，一次国数的值小子辰比例函数的值.120、(2015?黄石)已知双

19、曲线y=x(x>0),直线Jy-J2=k(x-72)(k<0)过定点F且与双曲线交于A,B两点，设A(Xi,yi),B(X2,y2)(xiVX2),直线I2：y=-x+"2.(1)若k=-1,求AOAB的面积S;52(2)若AB=2，求k的值；(3)设N(0,242),p在双曲线上，M在直线I2上且PM/x轴，求PM+PN最小值，并求PM+PN取得最小值时P的坐标.(参考公式：在平面直角坐标系中，若A(xi,yi),B（X2,y2）则A,B两点间的距离为AB=V（X1x2）（y1力）（2）根据题意得:整理得：kx( 1-k) >：-1 = 0=G1F>2(ix

20、i*解：(1)当k=lB九li：y=-x+20,j=-x-2"联立得，_19化简得x2px+l=0,一解得：x=j2-l>x;=J3+l,设直线1与y轴交于点C,则C(0,2).1SAoA=SAACC-SA=oc=-B22b(xz-x)=2J2;(k<0)，=(!<)2-4XkX(-1)=2(1+k2)>0,，X、X2是方程的两根,AB=j(.n-x2)2-(ji-v2)2=(戈1一工2)-(±一=(x1)2-4r1>.Y2(1-777-7)*x|XpA?将代入得，AB=N二十I，、0m(k<0)5Jk2T一k2整理得；2kz+5k+2=

21、0,解得：k=-2»或k=i?(3)F,如图：设P(x,-),则M(-+K,-),XJC'JC则PM=k+L-4(xvPF=CL。)""加工工2_二_2Mx-»+4,.'.PM=PF.-.PM+PN=PF+PNNF=2,当点P在NF上时等号成立，此时NF的方程为y=-x+2,由（1）知PJI+1），.当Pgl,pl）时，PM+PN最小值是2.（2015?孝感）如图，4AOB是直角三角形，/AOB=90,OB=2OA，点A在反比例函数y=x的图象上.若点B在反比仞函数y=x的图象上，则k的值为（,把一个直角三角尺 DEF放在 OAB内，使其

22、斜边FD在线段AB上，三角尺可沿着线段AB上下滑动.其中/ EFD=30(1)求直线ED=2，点G为边FD的中点.AB的解析式；(2)如图1,当点D与点A重合时，求经过点 G的反比例函数y= x (kwo)的解析式;解1过点A，E作&匚_Lx轴，BDIk轴，分别于孰D.设点人的坐标是（a,H）,则OC=m,VZAOB=&0*,ZAOC+ZBCD=90n,/ZDBO+ZBOD-90'，:ZBfiO=ZAOC*/ZBDO=ZACO=BO'，；EDQs4OC息,.RD=OD_OB,QE二M，BI）=2jh»OD=2n，因为点A在反比例函教的图象上，则im=L

23、；点日在反比例函数”X的粥藁上，E点的坐标是2m）,x:*k=-2nl2m=_4mrL=-4*22、（2015?宜昌）如图，已知点A（4,0）,B（0,4、'在三角尺滑动的过程中，经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式；如果不能，说明理由。）(3)图1斛：(1)设直线AB的解析式为y=kx+b,VA(4,0),E(0,4j3),'4攵-b=0>6=44，假作1%=一。y=->3x+4AJ;3=4。，直线AB的解析式为:(2)J在RSDEF中“ZEFD=30b，ED=2,EF=2伺DF=4,二点D与点A重合，/.D(4,0),A

24、F(2,2,.*.G(3,用，管反比例函数y=8经过点G,Xk=3p,二反比例函数的解析式为：广士叵x13)建过点G的反比例函数的图象能同时经过点F；理由如下:丁点F在直线AB上，二设f(t,-JTt+qp),XVED=2f/.D(t+2,-t+2p),丁点G为边FD的中点.（3）经过点C的反比例函数的图辣能同时经过点F：丁点F在直线上，设FCt-,51VED=23ADL+2,-技斗2，1点G为边FD的串点.二G3+3,若过点G的反比例函数的图源也经过点F，设解析式为厂生.XF30T则1u,rr-用理由如下整理得：（-（3+3J3）ct+n=（-用+）心解得；6*5经过点G的反比例函数的图象能

25、同盹蛭过点F,这个反比例函数解析式为！厂三E.4K（2015?咸宁）如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折线”）.（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；（2）如图2,双曲线y=x与新函数的图象交于点C（1,a）,点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与新函数图象交于另一点E,与双曲线交于点P.试求PAD的面积的最大值；探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的1,则点（-4,-1）关丁K轴的对称点为（-4，1）.

26、把（-4,1）,（-3,0）代入y=kx+b,z_（7k-b=1伙=-1将，解伐*,，1-3左-6=01b=-3y=-x-3综上所述，新函数的解析式为y=p-'-3（空?V=-v-3（.x<-3）（2）如图2,;点C（1,a）在直线y=x+3上，：a=1+3=4. 点C（1,4）在双曲线丫=&上，Xk=1X4=4>y=".x,点D是线段AC上一动点（不包括端点）， 可设点D的坐标为（m,m+3）,且 DPx轴，且点P在双曲线上，：.?（二，m+3）,加一3.PD=?-m,洲一3 PAD的面积为S=:（7-血）X（m+3）=一：曲"一春111+2=

27、-2（m+三）2w-3222287a=-1<0, 当m=-彳时，S有最大值，为十，2oapAD的面积的最大值为温；W在点D运动的过程中，四边形PAEC不能为平行四边形.理由如下：当点D为AC的中点时，具坐标为（-1，2）,此时P点的坐标为（2,2）,E点的坐标为（-5,2）,VDP=3,DE=4,EP与AC不能互相平分，四边形PAEC不能为平行四边形.a24、(2015?宁波)如图，已知点A,C在反比仞函数y=x(a>0)的图象上，点B,Db在反比仞函数y=x(b<0)的图象上，AB/CD/x轴，AB,CD在x轴的两侧，AB=3,CD=2,AB与CD的距离为5,则a-b的值是

28、()。25、(2015?宁波)如图1,点P为/MON的平分线上一点，以P为顶点的角的两边分别与射线OM,ON交于A,B两点，如果/APB绕点P旋转时始终满足OA?OB=OP2,我们就把/APB叫做/MON的智慧角.(1)如图2,已知/MON=90，点P为/MON的平分线上一点，以P为顶点的角的两边分别与射线OM,ON交于A,B两点，且/APB=135.求证：/APB是/MON的智慧角.(2)如图1,已知ZMON=(0°<“V90°),OP=2.若/APB是/MON的智慧角，连结AB,用含a的式子分别表示/APB的度数和4AOB的面积.3(3)如图3,C是函数y=x(x

29、>0)图象上的一个动点，过C的直线CD分别交x轴和yA, B两点，且满足 BC=2CA，请求出Z AOB的智慧角Z APB的顶点P的坐标11）证明，=，成可=9。°，P为NMON的平分线上一点,.,.ZAOP=ZBOP=izMOJT=45",VZAOP-t-ZOAP+ZAPO=180，.*.Z0AP+ZAP0=135",VZAPB=135",.ZAPO+ZOPB=135B,AZ0AP=Z0PB,AAOPAPOB,.O-OP''OPOB'.*.OP2=OAfcOB,.NAPE是NMON的智31角;2）解：NAPB是NMOM的智

30、茗角，-,.OA*OB=OPS.OA=OP,'OPOB"；P为NMOM的平分线上一点，.-ZAOP=ZBOP=a，/.AAOPAPOB,.ZOAP=ZOPB,-,.ZAPB=ZOPBi-ZOPA=ZOAP+ZOPA=180'-1a,BnZAPB=180°-；Qj过点A作AHLOB干出连接AB;如图1所示，贝”遍金09如=1090人,正（1"OP，sina,0JV0P=2,*SAAC=2sir.ct；（3）设点C（a.b）,则ab=3,过点C作CH10A于H；分原种情况:当点B在y轴正半轴上时；当点A在x轴的负半轴上时，如图2所示:BC=2CA不可能

31、；当得A在x轴的五半轴上叶，如图3所示VBC=2CA,.CA=1"ABTVCII.70B,:.AACHAABO,.CH_AH=CA：l市OAABTOB=3b,04=单 cazn3aov9ab27 0Aw0B=-3b=-=,TNAPb是NAOB的智急用，0P=JCUO5=F=半，,.,ZAOB=90',OP平分NAOB, 点F的坐标为：（土£,事）；图4当点B在y轴的负半柏上时，如困4所示:VBC=2CA,在2达日和白人80中，Zahc=Zaob<£bao=£cah，CA=AB：.AACHAABO（AAS）,/.OB=CH=b>OA=A

32、H=1a,O4OB=b=jNAPB是NAOB的智慧角,OP=JO,OB二VZAOB=90",OP平分/AOB,点P的坐标为，（卓，-g）>综上所述：点p的坐标为:（淮,孚），或（W,-£）.222一解：丁乩点的坐标为y，a）-根据题:意6Ca-1!a-1Js3,3当C在双曲线丁=：工>口）时，则5】二七了解得a=JJ+1*当人在取曲笠y=L：K>G）时，则"士ra解得斫二a的取值范B1是故答案为JI石28、（2015?湖州）如图，已知在平面直角坐标系xOy中，。是坐标原点，点A是函数y=x（x<0）图象上一点，AO的延长线交函数y=x（x&

33、gt;0,k是不等于0的常数）的图象于点C,点A关于y轴的对称点为A',点C关于x轴的对称点为C,交于x轴于点B,连结AB,AA',AC：若4ABC的面积等于6,则由线段AC,CC,CA；AA所围成的图形的面积等于（）B.10解！过A作M_LY轴子D,连援GM，丁点A是函数广二（x<0）图象上一点，x工设A（a,）ia丁点C在语数汴二（x>0,k是不等于口的常数）的图象上X1.,.设C（b,二），bVAD1BD,BC_LBD,.'.AOADA6C0,.SAADO_.ODA2_k 9、（ 2015?丽水）如图，反比例函数 y= X的图象经过点（-1, -2、&

34、#39;2）,点A是该图象第一象限分支上的动点，连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC ,顶点C在第四象限，AC与x轴交于点P,连结BP.（1） k的值为（）.（2）在点A运动过程中，当 BP平分/ABC时，点C的坐标是（）。-='I411-1='1Ssos产1L.2VS£kADC=T-SA=OC=i¥n*=第i01r.-SiABC=SAACB+Siec：=L-J+2_=6,2a2-5二k=二12,£L"+k-12=0,解德ik=3,k二7不台题意舍去），；点4关于若由的对标点为A，,点C关于x轴的对称点为C，

35、.'.Z1=Z2,Z3=Z4,/.Zl+Z4=Z2-hZ3=?5",：.0N，OC：在同一条直线上.M9"-S£ic=cSAoec=-=t?VSA；aji.-2SA；ae=1，上由线段AC，CC'，出，A-防围成的图形的面枳二S&qf+SAm：+民=1口.解：（1）地点（T，代人反比例函物产&得：.1k=-lXL2p）二平他答案知:2JL（2）连接0C，作AJI_L又抽干MCWJLx轴干的如图所示：则AI4C见ZA10=ZONC=90"，.'.ZA0M+Z0AM-9C",根据题意彳船点且和点日关于原点对称

36、，AOAOBtV是等腰直角三角形，AB为斜边，AOC-LAB（三线合一），OC=1AB=OA,AC=BC,AB=j2BC,ZAOC=£QB，I|IZAOOZCON=90,/.ZOAHfZCONi在ADAM和ACON中，Zamo=Zoxc<ZOAM=ZCOXOA=OC.&QAMKACQN（AAS）+，ON=CN，止oh,YBP平分上ABC.,AP_A3_S2iBJCPBC1VAI/CN,a，n=-4"cyc?Tf设CM=OM=k,则AM=0M=耳，,点A在反比例函数空匕二0M旬三邛，即又，.二平解解，=c,二cmJI，0N=2,二点c的坐标为I13-JJ故答案为

37、；（2,-）.30、（2015?烟台）如图，矩形OABC的顶点A、C的坐标分别是（4,0）和（0,2）,k反比例函数y=x（x>0）的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则4ODE的面积为（）。解；二四边形04B匚是矩形,AB-OC,BC=OL丫机C的坐标分别是（40）和（和Z）JbOA=4*GB=2*丁户是矩形对角统的交点，二P31）,:反比例函数y二三（x0）的图建过对角蜡的交点F，X，k=2i，反比例函救的解析式为；尸工X二.D,E两点在反比例函数好占行。）的图辗的图象上，x二口（%，E口，2）1,"3"4w,3阴品二跋

38、形一沁同口口§cof-SAede=4X2-lx2-ix;-lx2x3二号.故答案为二号.k231、（2015?青岛）如图，正比例函数y产kix的图象与反比例函数y=x的图象相交于A,B两点，其中点A的横坐标为2,当yiy2时，x的取值范围是（）。且,工式一2或kA2E.冥式一？或口玄耳玄2C.一2V再VQ或Q（耳一2D,-2芯0或耳2kk直线y=k2x与反比例函数y= x的图象交于点 C, D,且ki?k20, kik,顺次连接 A, D,若不能，请简要说明理由.3 2、（ 2015?威海）如图1,直线y=kix与反比例函数y= x （kWO）的图象交于点A, B,B, C, AD

39、, BC分别交x轴于点F, H ,交y轴于点E, G,连接FG , EH .（3）如图3,若四边形 EFGH为正方形，点 A的坐标为（2, 6）,求点C的坐标;（4）判断：随着 七、k2取值的变化，四边形 ADBC能否为正方形？若能，求点 A的坐标;(1)四边形ADBC的形状是（）；（2）如图2,若点A的坐标为（2,4）,四边形 AEHC是正方形，则k2二（）；解：丁反比洌函数与正比例函数的图象均关于原点对称，.二A、E两点美干原点对称,点A的横坐标为露二点B的横坐标为-2，由函数图象可知，当或耳2时函数的图建在工的上 X方，当方了工时，X的取值范围是-2式。或耳2.故选D.解:(1)正比例函数与反比例函数的图莪均关于原点对称，/.OA=OB»OC=OD,四边形ADBC是平行囚边形.故答猱为:平行四边形；(2)如图1,过点A作轴，垂足为M,过点C作CN_Lx轴，垂定为N,;四边形AEHC是正方形，/.DA1AC,二四边形ADbC是矩形，OA=OC.AM=CfhAC(4,2),2=4k解得k2=g.故答案为；龙图3所示，过点A作AMJLy轴，垂足为N,过点C作CNlx舶，垂足为N,丁四边形EFGH为正方形，AZFE0=45e,EO=HO,.,.ZAEH=45*.VZAME=90*,AZEAM=ZAEM=45e. AM=EM.图2同理，CN=HN. 点A