《函数的最值与导数》

1、函数的最大函数的最大(小小)值与导数值与导数 (1) 求函数的定义域求函数的定义域 (2) 求导函数求导函数f(x)； (3) 求解方程求解方程f(x)=0； (4) 检查检查f(x)在方程在方程f(x)=0的根的左右的根的左右的符号，并根据符号确定极大值与极小值的符号，并根据符号确定极大值与极小值. .口诀：口诀：左负右正为极小，左正右负为极大左负右正为极小，左正右负为极大. .1. 1. 用导数法求解函数极值的用导数法求解函数极值的步骤：步骤： 复习复习 一般地，设函数一般地，设函数y=f(x)的定义域为的定义域为I，如果存在，如果存在实数实数M满足：满足： 1) ) 最大值最大值: :

2、（1）对于）对于任意任意的的xI，都有都有f(x) M; （2）存在存在x0 I，使得，使得f(x0) = M那么，我们称那么，我们称M是函数是函数y=f(x) 的的最大值最大值 2.最值的定义最值的定义极大值极大值0(1)()0fx(2)如果如果在在x0附近附近的的左侧左侧 ,右侧右侧 那么那么f(x0) 是极大值是极大值( )0fx ( )0fx 2) 2) 最小值最小值: : 一般地，设函数一般地，设函数y=f(x)的定义域为的定义域为I，如果存在，如果存在实数实数M满足：满足： （1）对于）对于任意任意的的xI，都有都有f(x) M; （2）存在存在x0I，使得，使得f(x0) = M

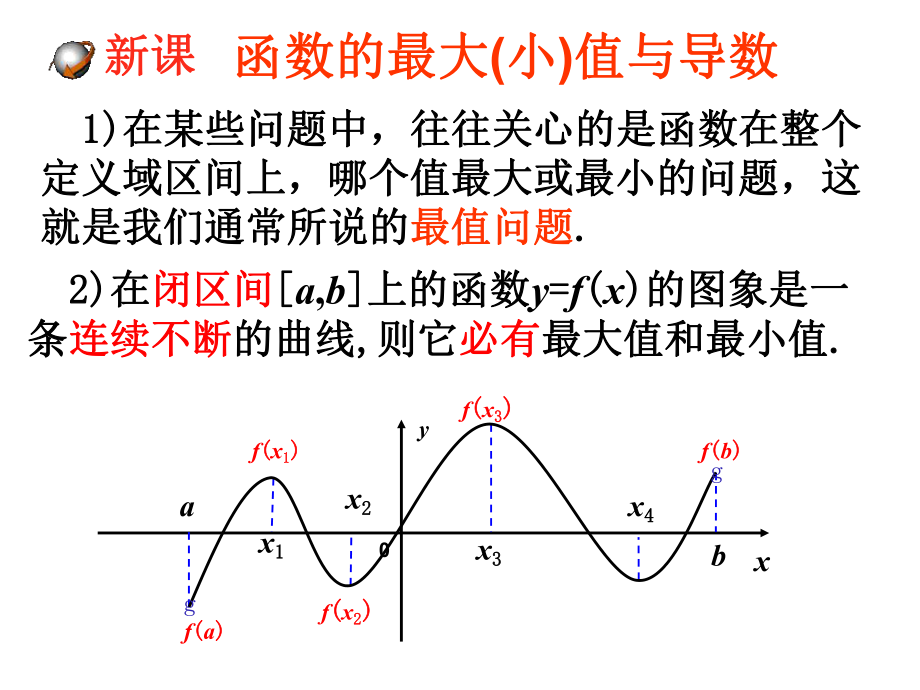
3、那么，我们称那么，我们称M是函数是函数 y=f(x) 的的最小值最小值 极小值极小值0(1)()0fx(2)如果如果在在x0附近附近的的左侧左侧 ,右侧右侧 那么那么 f(x0) 是极小值是极小值( )0fx ( )0fx 函数的最大函数的最大(小小)值与导数值与导数 1) 1)在某些问题中，往往关心的是函数在整个在某些问题中，往往关心的是函数在整个定义域区间上，哪个值最大或最小的问题，这定义域区间上，哪个值最大或最小的问题，这就是我们通常所说的就是我们通常所说的最值问题最值问题. . 2)2)在在闭区间闭区间 a,b 上的函数上的函数y= =f( (x) )的图象是一的图象是一条条连续不断连

4、续不断的曲线的曲线, ,则它则它必有必有最大值和最小值最大值和最小值. .xy0abx1 1x2 2x3 3x4 4f( (a) )f( (x3 3) )f( (b) )f( (x1 1) )f( (x2 2) )gg 新课新课oxyaboxyaboyoxyaby= =f( (x) )y= =f( (x) )y= =f( (x) )xaby= =f( (x) )函数在开区间函数在开区间(a, b)内内不一定有最值不一定有最值 思考：如果在没有给出函数图象的情况下，思考：如果在没有给出函数图象的情况下，怎样才能判断出怎样才能判断出f(x3)是最小值是最小值, 而而f(b)是最大值呢？是最大值呢？

5、 y=f(x)观察下面这个定义在区间观察下面这个定义在区间a,b上的函数上的函数y=f(x) 的的图象：图象：xoab by1x2x3x发现图中发现图中_是极小值，是极小值，_是极大值，是极大值，在区间上的函数的最大值是在区间上的函数的最大值是_，最小值是，最小值是_。13(),()f xf x2()f x( )f b3()f x (2) 将将y=f(x)的各极值与的各极值与f(a)、f(b)( (端点处端点处) )比较比较, ,其中最大的一个为最大值，最小的一个最小值其中最大的一个为最大值，最小的一个最小值. . 求求f(x)在在闭区间闭区间a,b上的最值的步骤上的最值的步骤(1)(1)求求

6、f(x)在区间在区间(a,b)内极值内极值( (极大值或极小值极大值或极小值) )解解:24yx 当当 变化时变化时, 的变化情况如下表的变化情况如下表:,yy 例例1、求函数、求函数 在区间在区间 上的最上的最大值与最小值。大值与最小值。0,3令令 ,解得解得0y 22或xx x（舍去舍去）20(0,2)(2,3)x( )f x ( )f x0343 极小值极小值4131443yxx在区间在区间0,3上，当上，当x=0时，函数的最大时，函数的最大值为值为4，当，当x=2时，最小值为时，最小值为43例2：已知函数已知函数(1)求求 的单调减区间的单调减区间(2)若若 在区间在区间 上的最大值为

7、上的最大值为 , 求该求该 区间上的最小值区间上的最小值( )f x( )f x 2,2 20所以函数的单调减区间为所以函数的单调减区间为(, 1)(3,)， 解解:2(1)( )369f xxx ( )0令f x 23690即xx 13解得:或xx 32( )39f xxxxa 2(2)( )369f xxx 令令 解得解得( )0f x 13或xx （舍去）（舍去） x( )f x( )f x ( 2, 1) 1 ( 1,2) 205 a 2 2 a 22 a 2220a2即a 最小值为最小值为527 例2：已知函数已知函数(2)若若 在区间在区间 上的最大值为上的最大值为 ,求该区间上的

8、最小值求该区间上的最小值32( )39,f xxxxa ( )f x 2,2 20所以函数的最大值为所以函数的最大值为 ,最小值为最小值为(2)22fa ( 1)5fa 当当 变化时变化时, 的变化情况如下表的变化情况如下表:( ),( )fxf x x解解:2(1)( )33f xx 令令 解得解得( )0f x 11或xx 所以函数的极大值为所以函数的极大值为 ，极小值为，极小值为 2 a 2 a 当当 变化时变化时, 的变化情况如下表的变化情况如下表:( ),( )fxf x x- + x( )f x( )f x ( 2, 1) 1 ( 1,1) 1(1,3)0-2 a 2 a 0极小值

9、极小值极大值极大值3( )3, 2,3f xxxa x (1)求求 的极值的极值(2)当当 在什么范围内取值时，曲线在什么范围内取值时，曲线 与与 轴总有交点轴总有交点( )f xxa( )yf x 例例3：已知函数已知函数218即a2a 18a 曲线曲线 与与 轴总有交点轴总有交点x( )yf x 20180aa 由（由（1）可知，函数在区间）可知，函数在区间 上的极大值上的极大值为为 ，极小值为，极小值为 ，又因，又因 ， 2a ( 2)2fa(3)18fa 2,3 2a (2)所以函数的最大值为所以函数的最大值为 ，最小值，最小值为为例例3：已知函数：已知函数(2)当当 在什么范围内取值

10、时，曲线在什么范围内取值时，曲线 与与 轴总有交点轴总有交点3( )3, 2,3f xxxa x xa( )yf x 练习：练习：1 1.函数函数 的最大值为的最大值为( )( )cos ,0,2f xxx x.0632ABCD2.2.函数函数 在区间在区间 上的最大值是上的最大值是 ，最小值是最小值是 ，若，若 ，则，则 ( )( )( )yf x , a bMmMm( )fxA. 等于等于0 B. 大于大于0 C.小于小于0 D.以上都有可能以上都有可能3 3.若函数若函数 ，则，则 （ ）3( )6 12f xxx( )f xA.最大值为最大值为22，最小值为，最小值为2B.最大值为最大值为22，无最小值，无最小值C.最大值为最大值为-22，最小值为，最小值为2D.即无最大值也无最小值即无最大值也无最小值DC2.( )ln2 ,1,f xxxxe4 函数在区间上的最大值为_.5.( ) 1,2_.xxf xe函数在区间上的最小值为0e (2) 将将y=f(x)的各极值与的各极值与f(a)、f(b)( (端点处端点处) )比较比较, ,其中最大的一个为最大值，最小的一个最小值其中最大的一个为最大值，最小的一个最小值. . 求求f(x)在在闭