初中数学圆中最值定值问题专题(推荐)

1、初中数学圆中最值定值问题专题（推荐）圆中最值域定值问题研究类型一、例1、如图，AB是。O的直径，AB=10cm,M是半圆AB的一个三等分点，N是半圆AB的一个六等分点，P是直径AB上一动点，连接MP、NP,则MP+NP的最小值是1、已知圆。的面积为3,AB为直径，弧AC的度数为80度，弧BD的度数为20度，点P为直径AB上任一点，则PC+CD勺最小值为2、如图，菱形ABC中，/A=60度，AB=3,圆A、圆B的半径为2和1,P、E、F分别是CD圆A和圆B上的动点，则PE+PF的最小值为类型二、折叠隐圆【基本原理】（一箭穿心）点A为圆外一点，P为圆。上动点，连接AO并延长交圆于Pi、P2,则AP

2、的最小值为AR,最例、如图4,在边长为2的菱形ABCD中，/A=60°,M是AD边的中点，N是AB边上一动点，将AMN沿MN所在的直线翻折得到AMN,连接A'C,请求出A'B长度的最小值.1、已知一个矩形纸片OACB将该纸片放置在平面直角坐标洗中，点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合)，经过点。P折叠该纸片，则CB的最小值为32、四边形ABCM,AD/BC,/A=90,AD=1,AB=2,BC=3,P是线段AD上一动点，将4AB啪BP所在直线翻折得到QBP则CQ曲面积最小值为始终为BD的中点，则将线段 CF最大值为类型三、随动位

3、似隐圆例、在RtABC中,/ACB=90,/BAC=30,BC=6.点D是边AC上一点D且AD=2卮将线段AD绕点A旋转得线段AD,点F分析:易知D'轨迹为以A为圆心AD为半径的圆，则在运动过程中AD'为定值2>/3,故取AB中点G,则FG为中位线，FG=1AD'=J3,故F点轨迹为以G为圆心，J3为半径的圆。2问题实质为已知圆外一点C和圆G上一点F,求CF的最大值。1思路2:倍长BC到B',则CF为B'D'的中位线，CFB，国B，最大时，CF也取最大值，问题实质为D在圆A上运动至彳S处时，BD取最大。【方法归纳】、如图，点A和点O1为定点

4、，圆Oi半径为定值，P为圆Oi上动点，M为AP中点？点M运动轨迹为圆O2,且O2为AOi中点。、构造中位线1、如图，在RtABC中，ZACB=90°,D是AC的中点，M是BD的中点，将线段AD绕A点任意旋转（旋转过程中始终保持点M是BD的中点），若AC=4,BC=3,那么在旋转过程中，线段CM长度的取彳1范围是2、如图，ABC是边长为2的等边三角形，以AC为直径作半圆，P为半圆上任意一点，M为BP中点，则在点P由A至ijC运动过程中，点M运动路彳5长为类型四、定性分析一一垂线段最短例、如图，半圆。的半径为1,AC±AB,BD，AB,且AC=1,BD=3,P是半圆上任意一点，

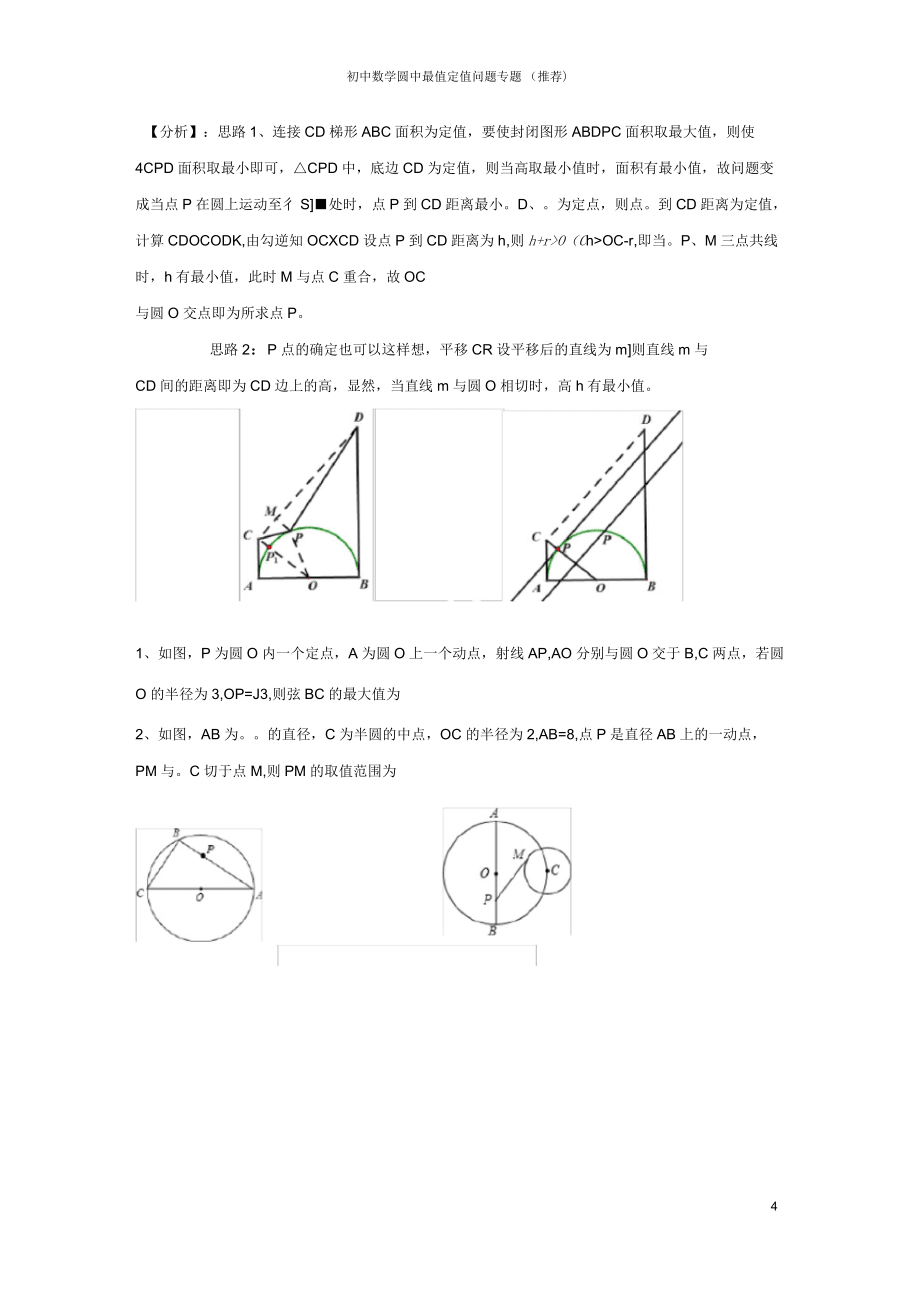
5、则封闭图形ABDPC面积的最大值是初中数学圆中最值定值问题专题（推荐）【分析】：思路1、连接CD梯形ABC面积为定值，要使封闭图形ABDPC面积取最大值，则使4CPD面积取最小即可，CPD中，底边CD为定值，则当高取最小值时，面积有最小值，故问题变成当点P在圆上运动至彳S处时，点P到CD距离最小。D、。为定点，则点。到CD距离为定值，计算CDOCODK,由勾逆知OCXCD设点P到CD距离为h,则h+r>O（Ch>OC-r,即当。P、M三点共线时，h有最小值，此时M与点C重合，故OC与圆O交点即为所求点P。思路2：P点的确定也可以这样想，平移CR设平移后的直线为m则直线m与CD间的距

6、离即为CD边上的高，显然，当直线m与圆O相切时，高h有最小值。1、如图，P为圆O内一个定点，A为圆O上一个动点，射线AP,AO分别与圆O交于B,C两点，若圆O的半径为3,OP=J3,则弦BC的最大值为2、如图，AB为。的直径，C为半圆的中点，OC的半径为2,AB=8,点P是直径AB上的一动点，PM与。C切于点M,则PM的取值范围为类型五、定弦定角【基本原理】如图。0中，A、B为定点，则AB为定弦，点C为优弧上任一点，在C点运动过程中则/ACB的度数不变？逆运用？如图2、点A、B为定点，点C为线段AB外一点，且/ACB二0（0为固定值）？点C在以AB为弦的圆上运动（不与A、B重合）图1图25例、

7、如图，AB为定长，点C为线段AB外一点，且满足/ACB=60度，请在图中画出点C的运动轨迹，简要说明作图步骤步骤1、步骤2、练习、1、如图，AB为定长，点C为线段AB外一点，且满足/ ACB=120度，请在图中画出点C的运动轨迹，并写出圆心角/AOB=2、如图，AB为定长，点C为线段AB外一点，且满足/ACB=120度，请在图中画出点C的运动轨迹，【实战应用】例、如图，。的半径为1,弦AB=1,点P为优弧AB上一动点，AC±AP交直线PB于点C,则ABC的最大面积是1、如图，ABC是边长为2的等边三角形，D是边BC上的动点，BE，AD于E,则CE的最小值为2、如图，RtAABC中，A

8、B±BC,AB=6,BC=4,P是ABC内部的一个动点，且满足/PAB=ZPBC,则线段CP长的最小值为类型六、定弦定角一一反客为主例、如图，/XOY=45°,一把直角三角尺ABC的两个顶点A、B分别在OX、OY上移动，其中AB=10,那么点O到顶点A的距离最大值为点。到AB的距离的最大值为【分析】：题意中AB为定长线段在角的两边滑动，。为定点，滑动中C为动点，AB两点位置发生变化，点。到AB距离的最大值的确定有难度，若改变思路，借助物理中运动的相对初中数学圆中最值定值问题专题(推荐)性可知，若将ABC固定，将/XOY的两边绕AB滑动，与原题中运动效果等价，题目中数量关系不

9、会发生改变。问题则变为当点O在圆上运动至彳S处时，点。到AB距离最大。#1、如图，D,E分别为等腰直角三角形ABC的边AC、AB上的点，且DE=2亚，以DE为边向外作正方形DEFG则AF的最大值为2、如图，4ABC中，/ABC45°,AC=2,半径为J5的圆O始终过A、C两点，连接OB,则线段OB长的的最大值为类型七、定弦定角一一条件的确定例、如图，扇形AOD43,/AOD=90,OA=66点P为弧AD上任意一点（不与点A和D重合），PQLOD于点Q点I为OPQ勺内心，则当点P在弧AD上运动时，求I点运动路径长。.分析:由内心的基本结论知/PIO=90o+1/PHO=135为定角，但

10、其所2对的边。皿非定弦，连ID,易证AIOOID,ZOID=ZPIO=135°,且其所对的边为°D符合定弦定角条件，故I点轨迹为圆弧，问题易解。1、如图，边长为3的等边ABCHE分别为边BCAC上的点，且BD=CEADBE交于P点，则CP的最小值为2、如图，AC=3,BG=5,且/BAG=90°,D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE则CE的最小值为()类型八、隐切线例、已知A(2,0),B(4,0)是x轴上的两点，点C是y轴上的动点，当/ACB最大时,则点C的坐标为分析:将/ACB看作以AB为弦的圆上的角，则圆心在AB的垂直平分线上，当圆

11、心运动时，/ACB的大小也随之改变，又因为点C为为y轴上的点，所以可将点C理解为圆。与y轴交点。Y轴与圆。的位置关系有两种：相交或相切，当圆。与y轴相交时，记交点为Ci,当圆。与y轴相切时，记交点为C,如图所示，/AGb=/AC2B,由圆上的角大于圆外的角可知，/ACB>ZAC2B,故当圆。于y轴相切时，/ACB有最大值。考虑对称性可知，点C的位置有两个，y轴正半轴和y轴负轴上各有一个点。初中数学圆中最值定值问题专题（推荐）1、已知点A、B的坐标分别是（0,1）、（0,3）,点C是x轴正半轴上一动点，当/ACB最大时，点C的坐标为在RtAAB计，/BAC=30,斜边AB=2>/3,

12、动点P在AB边上，动点Q在AC边上，且/CPQ=90,则线段CQ长的最小值=例、已知A（2,0）,B（5,0）,点P为圆A上一动点，圆A半径为2,以PB为边作等边分析:思路1:要求AM的取值范围，则先确定M点运动轨迹。由等边三角形联想共顶点的双等边结构，可构造和PBMtt顶点B的等边ABHi则4AP四HBI?HM=PA=2点M运动轨迹为以H为圆心，半径为2的圆H上的点。AM过圆心时取得相应最大和最小值。思路2:线段BM可看作由线段PB绕点B顺时针旋转60度得到，当点P在圆A上运动时，作出其绕点B顺时针旋转60度后的每一个对应点，则其应点的集合就是点M运动轨迹。显然其轨迹为圆。因为每个对应点都是

13、点P绕点B顺时针旋转60度得到，所以点M所在圆的圆心即为将P点所在圆圆心A绕点B顺时针旋转60度得到。想象成钟摆绕点B顺时针旋转60度91、如图，已知A（2,0）,圆O半径为1,点B为圆O上一动点，点C在第一象限，且4ABC为等腰直角三角形，/BAC=90度，求线段OC的最大值2、如图，AB为。的直径，AB=4,点C为半圆AB上动点，以BC为边在。外作正方形BCDE（点D在直线AB的上方）连接 OD当点C运动时，则线段 OD的最大值为初中数学圆中最值定值问题专题(推荐)类型十、半径不确定的处理策略例、在ABC中,AB=4,BC=6/ACB=30°，将ABC绕点B按逆时针方向旋转，得到AIBCI点E为线段AB中点，点P是线段AC上的动点，在ABC绕点B按逆时针方向旋转的过程中，点P分析:显然BP=BP1,P1点轨迹为以B为圆心，BP为半径的圆，半径是多少呢？好象无法确定，因为点P为AC上动点，则BP长度有最小值和最大值。如图当BP垂直AC时，半径最小,当P与C重合时，半径最大，由图可知P1点轨迹为以B为圆心的无数个同心圆。不难确定其最小值和最大值1、在4ABC中，/ACB=90°,/ABC=30°,将4