北师大九年级上数学教案课程讲义重要

1、第一章 特殊的平行四边形§ 1,1 菱形的性质与判定一、 教学目标：.1、菱形的性质定理的运用.2.菱形的判定定理的运用.二、教学重点难点： 掌握菱形的性质推导及面积计算方法的推导，运用综合法解决菱形的相关题型。三、概念：菱形性质：1 .两条对角线互相垂直平分;2. 四条边都相等；3. 每条对角线平分一组对角;4. 菱形是一个中心对称图形，也是一个轴对称图形菱形的判定定理：1、有一组邻边相等的平行四边形是菱形定义2、对角线互相垂直的平行四边形是菱形.根据对角线3、四条边都相等的四边形是菱形.根据四条边4、每条对角线平分一组对角的四边形是菱形.对角线和角的关系四、讲课过程:1、例题、例

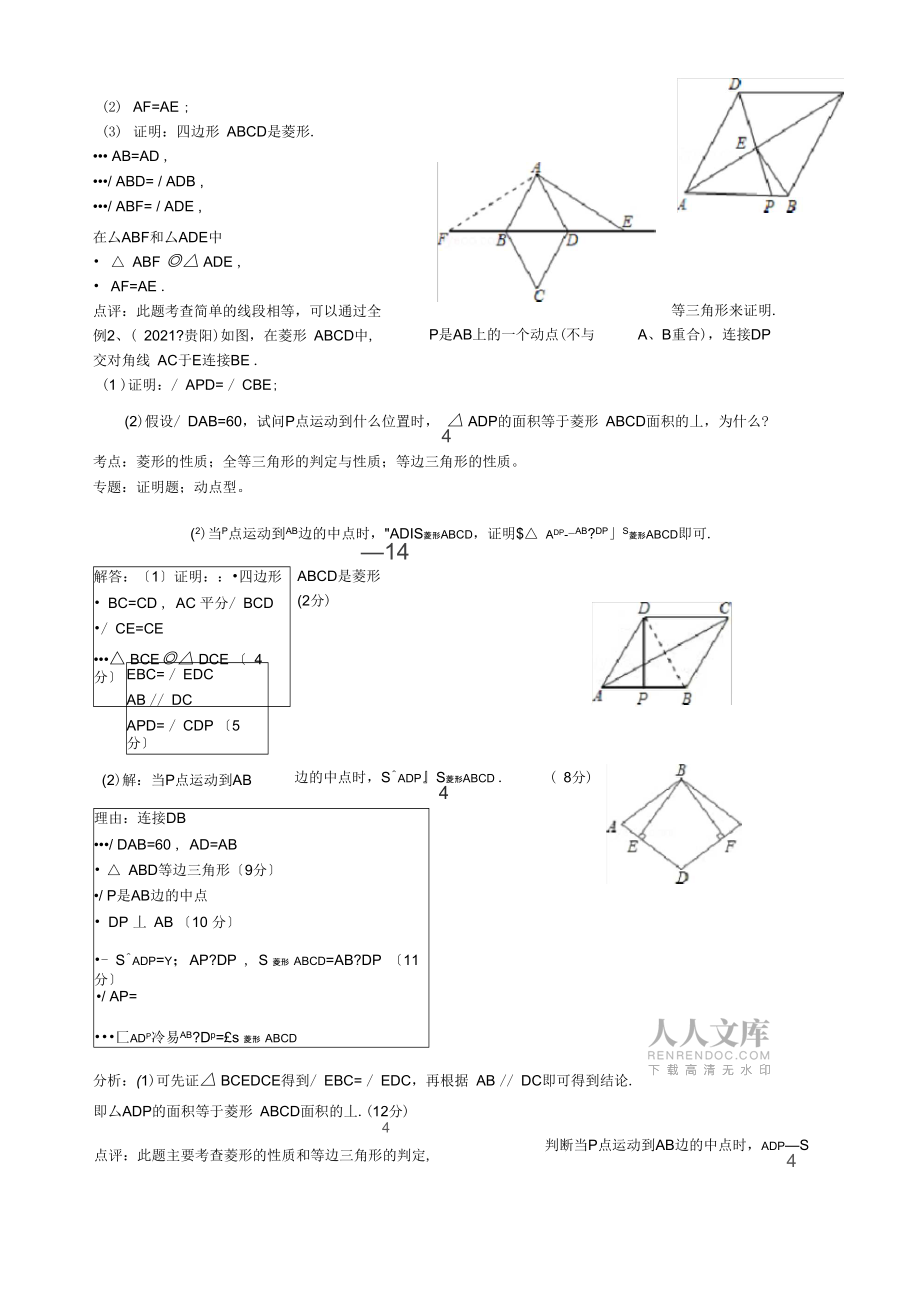
2、1. 2006?大连：如图，四边形 ABCD是菱形，E是BD延长线上一点，F是DB延长线上一 点，且DE=BF .请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜测并证明 它和图中已有的某一条线段相等只须证明一组线段相等即可.1连接 AF ;2 猜测：AF = AE ;3证明：说明：写出证明过程的重要依据 考点：菱形的性质；全等三角形的判定与性质。 专题：几何综合题。分析：观察图形应该是连接 AF，可通过证 AFB和厶ADE全等来实现 AF=AE . 解答：解：1如图，连接AF ;(2) AF=AE ;(3) 证明：四边形 ABCD是菱形. AB=AD ,/ ABD= / AD

3、B ,/ ABF= / ADE ,在厶ABF和厶ADE中 ABF ADE , AF=AE .点评：此题考查简单的线段相等，可以通过全 例2、( 2021?贵阳)如图，在菱形 ABCD中, 交对角线 AC于E连接BE .(1 )证明：/ APD= / CBE;P是AB上的一个动点(不与等三角形来证明.A、B重合)，连接DP(2)假设/ DAB=60，试问P点运动到什么位置时， ADP的面积等于菱形 ABCD面积的丄，为什么?4考点：菱形的性质；全等三角形的判定与性质；等边三角形的性质。专题：证明题；动点型。(2)当P点运动到AB边的中点时，"ADIS菱形ABCD，证明$ ADP-AB?

4、DPS菱形ABCD即可.解答：1证明：四边形 BC=CD , AC 平分/ BCD/ CE=CE BCE DCE 4 分又14ABCD是菱形(2分)EBC= / EDCAB / DCAPD= / CDP 5 分EBC= / APD 6 分(2)解：当P点运动到AB边的中点时，SADPS菱形ABCD .( 8分)4理由：连接DB/ DAB=60 , AD=AB ABD等边三角形9分/ P是AB边的中点 DP 丄 AB 10 分- Sadp=y；AP?DP , S 菱形 abcd=AB?DP 11 分1.1/ AP=匚ADP冷易AB?Dp=£s 菱形 ABCD分析：(1)可先证 BCED

5、CE得到/ EBC= / EDC，再根据 AB / DC即可得到结论.即厶ADP的面积等于菱形 ABCD面积的丄.(12分)4点评：此题主要考查菱形的性质和等边三角形的判定,判断当P点运动到AB边的中点时，adpS4例3、( 2021?宁洱县)如图，四边形 ABCD是菱形，BE丄AD、 垂足分别为E、F.(1) 求证：BE=BF;(2) 当菱形 ABCD的对角线 AC=8，BD=6时，求BE的长. 考点：菱形的性质；全等三角形的判定与性质。分析：(1)根据菱形的邻边相等，对角相等，证明 ABE与厶CBF据全等三角形对应边相等即可证明；(2)先根据菱形的对角线互相垂直平分，求出菱形的边长，再根据

6、菱形的面积等于对角线乘积的一 半和底边乘以高两种求法即可求出.解答：(1)证明：四边形 ABCD是菱形， AB=CB，/ A= / C,/ BE 丄 AD、BF 丄 CD ,/ AEB= / CFB=90 , 在厶ABE和厶CBF中， ABE CBF (AAS ), BE=BF .(2)解：如图，对角线 AC=8 , BD=6 ,对角线的一半分别为4、3,菱形的边长为.=5,菱形的面积=5BE=- X80,BF 丄 CD ,全等，再根解得BE=i.5点评：此题主要考查菱形的性质和三角形全等的证明，同时还考查了菱形面积的两种求法.例3、( 2021?广安)如下图，在菱形 ABCD中，/ ABC=

7、60 , DE / AC交BC的延长线于点 E. 求证：DE=BE.3考点：菱形的性质。专题：证明题。分析：由四边形 ABCD是菱形，/ ABC=60，易得BD丄AC ,Z DBC=30，又由DE / AC,即可证 得DE丄BD，由直角三角形斜边上的中线等于斜边的一半，即可证得DE=BE.解答：证明：法一：如右图，连接 BD ,四边形ABCD是菱形，/ ABC=60 , BD 丄 AC，/ DBC=30 ,/ DE / AC , DE丄BD, 即/ BDE=90 ,法二：四边形 ABCD是菱形，/ ABC=60 , AD / BC , AC=AD ,/ AC / DE ,四边形ACED是菱形，

8、 DE=CE=AC=AD ,又四边形ABCD是菱形， AD=AB=BC=CD , BC=EC=DE，即 C 为 BE 中点, DE=BC= 2bE.2点评：此题考查了菱形的性质， 直角三角形的性质等知识. 此题难度不大，注意数形结合思想的应用. 例4. 2021?益阳如图，在菱形 ABCD中，/ A=60 , AB=4 , O为对角线BD的中点，过 O点作 OE丄AB，垂足为E.1求/ ABD的度数；2求线段BE的长.考点：菱形的性质。分析：1根据菱形的四条边都相等，又/A=60°，得到 ABD是等边三角形，/ ABD是60°2先求出OB的长和/ BOE的度数，再根据30&

9、#176;角所对的直角边等于斜边的一半即可求出.解答：解：1在菱形 ABCD 中，AB=AD，/ A=60° , ABD为等边三角形， / ABD=60 ; 4 分2 由1可知 BD=AB=4 ,又 O为BD的中点， OB=2 6 分，又 OE丄AB，及/ ABD=60 , / BOE=30 , BE=1 . 8 分点评：此题利用等边三角形的判定和直角三角形30°角所对的直角边等于斜边的一半求解，需要熟练掌握.2、稳固练习1. 有一组邻边相等的平行四边形是2. 菱形的两条对角线长分别是 8 cm和10 cm,那么菱形的面积是3.菱形的两邻角之比为1： 2,边长为2,那么菱形

10、的面积为4.菱形的面积等于20 分A.对角线乘积B. 一边的平方 C.对角线乘积的一半 D.边长平方的一半5. 以下条件中，可以判定一个四边形是菱形的是20分A. 两条对角线相等B.两条对角线互相垂直C.两条对角线相等且垂直D.两条对角线互相垂直平分6. 菱形的两条对角线把菱形分成全等的直角三角形的个数是.20分A 1 个B 2 个 C 3 个 D 4 个7. 如图，四边形 ABCD是菱形，/ ABC=120 , AB=6cm那么/ ABD二,?/ DAC的度数为;对角线BD=, AC=;菱形ABCD勺面积为. 20分8、在矩形ABC中, 0是对角线AC的中点，EF是线段AC的中垂线，交AD

11、BC于E、F.求证：四边形 AECF是菱形20分9、如图，在菱形 ABC中, AB=BD=5求：1Z BAC的度数；2求AC的长10、四边形ABCD1矩形，四边形AECF是假设AB=2cm BC=4cm 求四边形AECF的面积11、在菱形ABCD中, E、F分别是BC CD上的点，/ EA交 FA于 H，交 AD于 G 假设/ BAE=25，/ BCD=130，求/ AHC的度数。疋菱形,D3、作业:一、选择题。1、 菱形两个邻角的比是1:5，高是8cm,那么菱形的周长是。A. 16cm B. 32cm C. 64cm D. 128cm2、 菱形的周长为40 cm，两对角线长的比是3:4，那么

12、两对角线的长分别是 。A. 6cm、8cm B. 3cm 、4cm C. 12cm 、16cm D. 24cm32cm 3、如图：在菱形 ABCD中, AEL BC, AF丄CD且E F分别为BC CD的中点，那么/EAF等于。A. 75 ° B. 60° C. 45° D. 30°4、棱形的周长为8.4cm，相邻两角之比为5： 1，那么菱形一组对边之间的距离为A、1.05cm B、0.525cm C、4.2cm D、2.1cm5、菱形具有而矩形不具有的性质是A.对角相等 B 四边相等C 对角线互相平分 D 四角相等& I口ABCD勺对角线AC

13、BD相交于点O,以下条件中，不能判定 口ABCD是菱形的 是 。A. AB=ADB.ACL BD C. / A=Z DD.CA平分/ BCD7、以下命题中，真命题是。A. 对角线相等且互相垂直的四边形是菱形。B. 有一条对角线平分一组对角的四边形是平行四边形。C. 对角线互相垂直的矩形是菱形。D.菱形的对角线相等。8、菱形是轴对称图形，对称轴有。A. 1条 B . 2条 C . 3条D. 4条9、 菱形的两条对角线长为 10cm和24cm,那么这个菱形的周长为,面积为10、将两张长10cm宽3cm的长方形纸条叠放在一起,使之成60度角,那么重叠局部的面积的最大值为.11、一个菱形面积为 80,

14、周长为40,那么两条对角线长度之和为 12、菱形 ABCD中, E、F 分别在 BC和 CD上,且/ B=Z EAF=60， / BAE=15，求/ CEF的度数。13、：如图，在菱形 ABC冲，E、F分别是BC CD上的点，且CE=CF过点C作CG/ EA交 AF于 H,交 AD于 G,假设/ BAE=25，/ BCD=130，求/ AHC的度数14、如下图，菱形1ABC冲 E 在 BC上，且 AB=AEZ BAE=i / EAD AE交 BD于 M 2试说明BE=AM15、如图，在 ABC中,AB=BCD E、F分别是BC AC AB上的中点,(1)求证四边形BDEF是菱形(2)假设AB=

15、12cm求菱形BDEF的周长?MEEDABHEGB'DFDCBD16、：如图， ABC中，/ BAC的平分线交BC于点D, E是AB上 一点，且AE=AC EF/ BC交AD于点F,求证：四边形CDEF是菱形。17.如图，平行四边形ABC啲对角线AC的垂直平分线与AD BC AC 分别交于点E、F、0,求证：四边形AFCE是菱形。18、：如图，C是线段BD上一点， ABCP ECD都是等边三角形，R、F、G H分别是四边形 ABDE各边的中点，求证：四边形RFGH是菱形。19、如图，在厶ABC中，AB=ACZ B，Z C的平分线 BD CE相交于点M DF/ CE EG/ BD, DF

16、与EG交于N,求证：四边形 MDN是菱形。§ 1,2 矩形的性质与判定、教学目标：1、能用综合法来证明矩形的性质定理和判定定理以及相关结论.2、能运用矩形的性质进行简单的证明与计算.、教学重难点： 矩形的性质的证明以及它与平行四边形的附属关系.三、概念：1.矩形的定义：有一个角是直角的平行四边形是矩形(矩 形是特殊的平行四边形)。2 .矩形的性质：矩形具有平行四边形的所有性质(1) 角：四个角都是直角。(2) 对角线：互相平分且相等。3 .矩形的判定:(1) 有一个角是直角的平行四边形。(2) 对角线相等的平行四边形。3有三个角是直角的四边形4. 矩形的对称性：矩形是中心对称图形，对

17、角线的交点是它的对称中心；矩形是轴对称图形，对称轴有 2条，是经过对角线的交点且垂直于矩形一边的直线5. 矩形的周长和面积：矩形的周长=2a b矩形的面积二长 宽二ab a,b为矩形的长与宽注意:1矩形被两条对角线分成的四个小三角形都是等腰三角形且面积相等。2矩形是轴对称图形，两组对边的中垂线是它的对称轴。四、讲课过程：【经典例题:】例1:：0是矩形ABCD寸角线的交点，E、F、G H分别是OA OB OC0D上的点，AE=BF=CG=DH求证：四边形 EFGH为矩形.分析：利用对角线互相平分且相等的四边形是矩形可以证明° 证明： ABCD为矩形 AC=BD AC BD互相平分于0

18、AO=BO=CO=DO AE=BF=CG=DHeo=fo=go=ho又 HF二EG.EFGH为矩形 例2:判断1两条对角线相等四边形是矩形2两条对角线相等且互相平分的四边形是矩形3有一个角是直角的四边形是矩形4在矩形内部没有和四个顶点距离相等的点分析及解答 ：1如图四边形ABCD中，AC=BD但ABCD不为矩形，.X2对角线互相平分的四边形即平行四边形，对角线相等的平行四边形为矩形" 3 如图，四边形ABCD中, Z B=90°,但ABCD不为矩形 /.X4矩形对角线的交点 0到四个顶点距离相等/X,如图，课堂练习题 : 】1判断一个四边形是矩形，以下条件正确的选项是A .

19、对角线相等 B .对角线垂直C.对角线互相平分且相等 D .对角线互相垂直 且相等。2. 矩形的两边长分别为10cm和15cm,其中一个内角平分线分长边为两局部，这 两局部分别为 A . 6cm 和 9cm B . 5cm和 10cm C . 4cm和 11cm D . 7cm 和8cmA.对角线互相平分且相等.四个角相等C.是轴对称图形.对角线互相垂直平分4在矩形ABCD中,对角线交于 0点，AB=0.6, BC=0.8, 那么 AOB的面积为；周长为5 一个矩形周长是12cm,对角线长是5cm,那么它的面积为 .6. 假设一个直角三角形的两条直角边分别为5和12，那么斜边上的中线等 于 .

20、7. 矩形的两条对角线的夹角是 60°，一条对角线与矩形短边的和为15,那么矩形对角线的长为 ，短边长为8. 矩形的两邻边分别为4 cm和3 cm,那么其对角线为 cm,矩形面积为9. 假设矩形的一条对角线与一边的夹角是 40 °，那么两条对角线相交所成的锐角是.10. 矩形的对角线相交所成的钝角为120°，矩形的短边长为 5 cm，那么对角线之 长为 cm。11. 矩形ABCD勺两对角线 AC与BD相交于O点，/ AOB二才BOC假设对角线 AC的 长为 18 cm，贝V AD= cm。12. ：如下图，矩形 ABCD中, E是BC上的一点，且 AE=BC ED

21、C 15 .【课后练习题A.对角相等B.对边相等C 对角线相等 D.对角线互1. 矩形具有而一般的平行四边形不一定具有的特征是相平分2. 如图，在矩形ABC冲，对角线AC与BD相交于点的面积3. ，矩形的一条边上的中点与对边的两个端点的连线互相垂直，且该矩形的周长为24 cm，那么矩形的面积为cm 2。贝EBC= 。5.如图, ABC中 , AB=AC D 为 BC上一点，DEI AB, DFL AC,BM为高,求证:DE+DF二B。4. 如下图，在矩形ABCD中，AB=2BC在CD上取一点E,使AE=AB6.如图,ABCD是矩形纸片，翻折/ B、/ D,使BC AD恰好落在 AC上。设F、H

22、上8仔C(1)求证：四边形 AEC(是平行四边形;分别是B D落在AC上的两点，E、G分别是折痕CE AG与AB(2)假设 AB= 4cm, BC= 3cm,求线段 EF的长。7、：如图，在 ABC中, AB=AC AD丄BC,垂足为点 D,人“是厶ABC的外角/CAM勺平分线，CEL AN垂足为点E,求证：四边形 ADCE为矩形。8、如图，在矩形 ABCD中 , AP=DC, PH二PC,求证:PB 平分 CBH.9、如图，矩形 ABCD中, E为AD上一点，EF丄CE交AB于F,假设DE=2矩形ABCD的周长为16,且CE=EF求AE的长.10、：如图，平行四边形 ABCD勺四个内角的平分

23、线分别相交于点E, F, G, H,求证：四边形 EFGH是矩形 11、：如图，四边形 ABCD是由两个全等的正三角形 ABD和BCD组成的，MN?分别为BC AD的中点.求证：四边形 BMDN是矩形.H分别是四边的12、如图，在四边形 ABCD中，AC DB交于O, E、F、G、中占I 八、7求证：四边形EFGH是矩形.§ 1,3 正方形的性质与判定一、教学目标：了解正方形的有关概念，理解并掌握正方形的性质和判定方法。二、教学重难点： 探索正方形的性质与判定。掌握正方形的性质和判定的应用方法三、概念：正方形的性质：1、正方形的四个角都是直角，四条边都相等2、 正方形的两条对角线相等

24、，并且互相垂直平分，每条对角线平分一组对角 正方形的判定:1、有一个角是直角的菱形是正方形2、有一组邻边相等的矩形是正方形。3、两组对边平行的菱形是正方形。4、对角线相等的菱形是正方形。5、对角线互相垂直的矩形是正方形。6、两组对边平行的矩形是正方形7、四边相等，有一个角是直角的四边形是正方形。8、一组邻边相等，对角线互相垂直的平行四边形是正方形。9、一组邻边相等且有一个角是直角的平行四边形是正方形。10、每个角都是90度的平行四边形是正方形。11、一组邻边相等，对角线平分的四边形是正方形。12、四个均为直角，每条对角线平分一组对角的四边形是正方形四、讲课过程1、例题例 1 :如图：MBC中，

25、/ACB=90 ,CD平分/ ACB,DE丄BC,DF丄AC,垂足分别为 E、F求证:四边形CFDE是正方形.分析：要证明四边形 CFDE是正方形，可以先证四边形 CFDE是矩形，然后再证明有一组 邻边相等；也可以先证四边形 CFDE是菱形，然后再证有一个角是直角.解 CD 平分/ ACB,DE 丄 BC,DF 丄 AC DE=DF角平分线上的点到角的两边的距离相等 / DEC= / ECF= / CFD=90 ,四边形 CFDE是矩形有三个角是直角的四边形是矩形，又 DE=DF 已证四边形CFDE是正方形有一组邻边相等的矩形是正方形.例 2：如图点 A、B'、C'、D'

26、;分别是正方形 ABCD四条边上的点，并且 AA'=BB'=CC'=DD' 求证：四边形A'B'C'D'是正方形分析：法一：先证明四边形AB'C'是3'菱形再证明四边形A'B'C'有一个角是直角法二：先证明四边形A'B'C'是3'矩形再证明四边形A'B'C'有一组邻边相等。证明：四边形 ABCD是正方形 AB=BC=CD=DA又A'A=B'B=C'C=D'D D'A=A'B=B&#

27、39;C=C'D/ A= / B= / C=Z D=90AA'D' 也厶 BB'A' CC'B' DD'C'AD'=AB'=BC'=CD'四边形A'B'C'D'是菱形又/ AD'A'= / BA'B' ,/ AA'D'+ / AD'A'=90° / AA'D'+ / BA'B'=90°D'A'B'=180° /A

28、A'D'+ / BA'B' =90°四边形A'B'C'D'是正方形例 3：如图：EG、FH过正方形ABCD的对角线的交点 O,EG丄FH,求证四边形EFGH为正方形解答：/正方形ABCDEG丄FH / OAH =Z OBE = 45o,DB=AC OA = OB, / AOH = 90o-Z AOE =Z BOE, " AOH 也"BOE ( ASA ) . OH = OE.同理 OE = OF = OG = OH,四边形EFGH是平行四边形 FH=EG EG丄FH?四边形 EFGH为正方形。2、稳固

29、练习1、如图，分别延长等腰直角OAB的两条直角边 AO和BO,使AO=OC , BO=OD求证：四边形ABCD是正方形2、矩形ABCD中，四个内角的平分线组成四边形3、判断以下命题哪些是真命题、哪些是假命题？对角线相等的菱形是正方形。 、对角线互相垂直的矩形是正方形。 、对角线互相垂直且相等的四边形是正方形。 、四条边都相等的四边形是正方形。 、四个角都相等的四边形是正方形。 、四边相等，有一个角是直角的四边形是正方形。 、正方形一定是矩形。 、正方形一定是菱形。 、菱形一定是正方形。EMFN，判断四边形EMFN的形状，并说明原因C 、矩形一定是正方形。4、：如图，正方形ABCDP, CM=C

30、D MNLAC连结CNJ那么/DCN5、在正方形 ABCDK AB=12 cm,对角线AC BD相交于0,那么厶ABO勺周长是()A.12+122B.12+6、2 C.12+2D.24+63、作业、21、在正方形ABCD的边BC的延长线上取一点 E,使CE=CA,连接AE交CD于 F,求 AFD的度数。变式：1、如以下图，正方形ABCDK E是CD边上的一点,F为BC延长线上一点，C匡CF(1)求证: BEC DFC (2)假设/ BEG60°，求/ EFD的度数.2:如图,E为正方形ABC啲BC边上的一点，CG平分/ DCF连结AE并在CG1取一点G,使EGAE求证：AEL EGc

31、3、P为正方形 ABCD3点，PA=1, PB=2, PC=3,求/ APB的度数.D4、(海南省)如图，P是边长为1的正方形ABCD寸角线AC上一动点(P与A C不重合)，点E 在射线 BC上，且 PE=PB(1)求证：PE二PD;PEL PDE(2)设AP=x, PBE的面积为y.求出y关于x的函数关系式,并写出x的取值范围;ABE CE与5、如图，四边形ABCD为正方形，以AB为边向正方形外作等边三角形DB相交于点F,贝y AFD二P6、 哈尔滨假设正方形 ABCD勺边长为4, E为BC边上一点，BE=3, M为线段AE上一点，射线BM交正方形的一边于点 F,且BF=AE那么BM的长为。

32、7、 .正方形的面积是1，那么其对角线长是 .38、E为正方形ABCD内一点，且 EBC是等边三角形，求/ EAD的度数.9、如图，正方形ABCD与正方形OMN的边长均为10，点0是正方形ABCD 的中心，正方形OMN绕0点旋转，证明：无论正方形OMN旋转到何种 位置，这两个正方形重叠局部的面积总是一个定值，并求这个定值.10、E是正方形ABCD对角线AC上一点，EF CD,EG AD,垂足分别为F、G,求证：BE=FG11、 RtVABC 中, C 90 , CD平分 ACB ,交 AB于 D, DF/BCQE/AC ,求证: 四边形DECF为正方形。第二章一元二次方程§ 2,1认

33、识一元二次方程一. 教学目标：1、经历方程解的探索过程，增进对方程解的认识，开展估算意识和能力。2、渗透“夹逼思想二. 教学重点难点：用“夹逼方法估算方程的解；求一元二次方程的近似解。三. 概念：一、一元二次方程定义含有一个未知数，并且未知数的最高次数是 2的整式方程叫做一元二次方程二、一元二次方程的一般形式ax2 bx c 0a 0，它的特征是：等式左边是一个关于未知数 x的二次多项bx叫做式，等式右边是零，其中ax2叫做二次项，a叫做二次项系数; 一次项，b叫做一次项系数；c叫做常数项。四. 讲课过程一、复习：1、 什么叫一元二次方程？它的一般形式是什么？ 一般形式：ax2+bx+c-0(

34、a丰0)2、指出以下方程的二次项系数，一次项系数及常数项。(1) 2x2x+1=0(2) x2+1=0(3)x 2x=0(4) 3 x 2=0二、新授：1、估算地毯花边的宽。地毯花边的宽x(m)，满足方程(8 2x)(5 2x)=18也就是：2x2 13x+11=0你能求出x吗？(1) x可能小于0吗？说说你的理由；x不可能小于0，因为x表示地毯的宽度2)x可能大于4吗？可能大于2.5吗？为什么？x不可能大于4，也不可能大于 2.5, x>4 时，52x<0 , x>2.5 时，5 2x<0.(3)完成下表x00.511.522.522x 13x+11从左至右分别11，

35、4.75，0， 4，乙一9(4)你知道地毯花边的宽 x(m)是多少吗？还有其他求解方法吗？与同伴交流。地毯花边1米，另，因82x比52x多3,将18分解为6X 3，82x=6，x=12、例题讲析：例：梯子底端滑动的距离 x (n)满足(x+6) 2+72=102也就是 x2+12x15=0(1)你能猜出滑动距离 x(m)的大致范围吗？2) x的整数局部是几？十分位是几？x00.511.522x +12x15-15-8.75-25.2513所以 1<x<1.5进一步计算x1.11.21.31.4x2+12x15-0.590.842.293.76所以 1.1<x<1.2因此

36、x的整数局部是1,十分位是1注意：(1)估算的精度不适过高。(2)计算时提倡使用计算器。三、稳固练习：1、判断以下方程是否为一元二次方程，如果是说明二次项及二次项系数、一次项及一次项系数和常数项:2 2(1) 2x+3x+5(2)( x+5)( x+2) =x+3x+1(3)( 2x-1 )( 3x+5) =-5(4)( 3x+1)( x-2 ) =-5x2、 把方程(3x+2) 2=4(x-3) 2化成一元二次方程的一般形式，并写出它的二次项系数、一次项系数和常数项。3、 关于x的方程(k-3 ) x2+2x-1=0，当k时，是一元二次方程。4、试找出五个连续整数，使前三个数的平方和等于后两

37、个数的平方和：?如果设五个连续整数中的第一个数为x，那么后面四个数依次可表示为、，根据题意可得方程：5、判断以下方程哪些是一元二次方程(1) 4x2 5x 1=x(2) 9x4- 5=0(3)丄 +x 5=3x ax 2+(b 1)x+c=0 (a 工 0) (5) 5(x 1)2=5x2 (6)x_ 1 0v'2 16、判断关于x的方程x2 nx(x n 1)=5x是不是一元二次方程，如果是，指出其二次项系数，一次项系数及常数项。7、 如果关于x的一元二次方程：x2 2(a+1)x+a2=0有两个整数根，a为整数，且12 v av 60，求这个方程的两个根。四、小结：估计方程的近似解

38、可用列表法求，估算的精度不要求很高。五、作业：1、五个连续整数，前三个数的平方和等于后两个数的平方和，你能求出这五个连续整数吗?2、一个面积为120平方米的矩形苗圃，它的长比宽多2米，求苗圃的周长?3、一名跳水运发动进行10m跳台跳水训练，在正常情况下，运发动必须在距水面 5m以前完成规定的动作，并且调整好入水姿势，否那么就容易出现失误。假设运动员起跳后的运动时间t(s)和运发动距水面的高度h(m)满足关系：h=10+2.5t-5t 2,那么他最多有多长时间完成规定的动作?4、两个数的和为10，积为9,求这两个数。5、把方程 2x(x-3)=(x+1)(x-2)+32化成 ax +bx+c=0

39、的形式后,a,b,c的值分别是A.3、 7、 1B.2、 -5、-1C.1、-5、-1D.3、-7、-16、方程x2-1=x;22x -y-1=0;243x - -+1=0;21中.其中是一元二5次方程的是(A. B.C.D.7、方程x2=x的解是A.1B.1或-1C.0D.18、在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形如果要使整个挂图的面积是5400亦，设金色纸边的宽为 xcm,那么满足的方程是(2A.x +130x-1400=0B.x22+65x-350=02C.x -130x-1400=0D.x2-65x-350=09、一元二次方程的一般形式是，二次项是

40、次项系数是10、方程3(x2-1)=x的二次项系数是，一次项是，常数项11、根据题意，列出方程：(1) 有一面积为54平方米的长方形，将它的一边剪短5米，另一边剪短2米,恰好变成一个正方形，这个正方形的边长是多少？(2) 三个连续的整数两两相乘， 再求和，结果为242,这三个数分别是多少？12、把以下方程化成一元二次方程的一般形式，并写出它的二次项系数、一次项系数和常数项:方程般形式二次项系数一次项系数常数项3x2=5x-1(x+2)(x-1)=64-7x 2=013、关于 x的方程(k2-1 )x2+2(k-1 )x+2k+2=0当k时是一元二次方程；当 k时是一元一次方程14、 关于x的方

41、程(k- -)x2+(m-3)x-1=0，是一元二次方程。那么k和m的取值范2围分别为什么？15、把以下方程化成一般形式，并写出它的二次项、一次项、常数项：(1) 9x2 4x=5(2)(x 7)(4x+3)=(x 1)2§ 2、2用配方法求解方程一. 教学目标： 21、会用幵平方法解形如(x+m) =n (n > 0)的方程;2、理解配方法，会用配方法解简单的数字系数的一元二次方程；3、体会转化的数学思想，用配方法解一元二次方程的过程。二. 教学重难点：理解并掌握配方法，能够灵活运用配方法解二次项系数为1的一元二次方程。如何利用等式的性质进行配方？三. 概念：1. 配方法：通

42、过配成完全平方式的方法得到了一元二次方程的根，这种解一元二闪方程的方法称为配方法2.配方法一般步骤：(1) 方程ax2 bx c 0(a0)两边同时除以a,将二次项系数化为1.(2) 将所得方程的常数项移到方程的右边。(3) 所得方程的两边都加上一次项系数一半的平方(4) 配方，化成(x a)2 b(5) 幵方。当b 0时，x a , b ；当b<0时，方程没有实数根。四. 教学程序：一、复习：1、解以下方程：(1) x2=9(2) (x+2) 2=162、什么是完全平方式？利用公式计算：2 1 2(1) (x+6)(2) (x - 2 )注意：它们的常数项等于一次项系数一半的平方。3、

43、解方程：(梯子滑动问题)2x +12x- 15=0二、新授：1、 引入：像上面第3题，我们解方程会有困难，是否将方程转化为第1题的方程 的形式呢？2、解方程的根本思路(配方法)女口： x2+12x 15=0转化为2(x+6)=51两边幵平方，得x+6= 土 51二 X1= 51 6x2= 51 6(不合实际)因此，解一元二次方程的根本思路是将方程转化为 (x+m)2=n的形式，它的 一边是一个完全平方式，另一边是一个常数，当 n0时，两边幵平方便可求 出它的根。3、讲解例题：2例1:解方程：X +8x9=0分析：先把它变成(x+m)2二n (n'O)的形式再用直接幵平方法求解。解：移项

44、，得：x2+8x=9配方，得：x2+8x+42=9+42(两边同时加上一次项系数一半的平方)2即: (x+4) =25幵平方，得：x+4= ± 5即: x+4=5，或 x+4= 5所以：X1=1， X2=9三、稳固练习:1、解以下方程:2(1)( 2-x ) =3 2(2)( x- . 2 ) =642 9(3) 2( x+1)工22(4) x -8x+9=0(5) x2- 7 x=232、配方：填上适当的数，使以下等式成立：(1) x2+12x+2=(x+6) 22(2) x 12x+=(x )2(3) x +8x+=(x+ )3、假设 x2=4,那么 x=假设(x+1) 2=4,

45、那么 x=假设 x2+2x+1=4,那么 x=2假设 x +2x=3，那么 x= 4、填上适当的数，使以下等式成立:2x +12x+=(x+6)2x -4x+=(x-)x2+8x+=(x+)5、利用配方法快速解以下两个方程:x 2+2x-35=05x22-15x-10=06、方程y2-4=2y配方，得(2A.(y+2) =6 B. (y-1)2=52C. (y-1)=3 D. (y+1)2=-3.四、小结:(1) 什么叫配方法?(2) 配方法的根本思路是什么?(3) 怎样配方?五、作业:1、如图，在一块长35m宽26m的矩形地面上，修建同样宽的两条互相垂直的道路，剩余局部种花草，要使剩余局部面

46、积为850，道路的宽应为多少？2、解以下方程：(1)x 2+12x+25=0(2)x 2+4x=10(3)x 2-6x=112(4) X -2x-4=02x-4x-12=02(6) x-10x+25=7(7) x2+6x=12X -6x-40=02(9)X -6x+7=02(10) x +4x+3=04、当x取何值时，代数式10-6x+x 2有最小值，是几?5、配方法证明y2-12y+42的值恒大于0。6、2(1) x -4x+(X-7、方程x2-12x=9964经配方后得X-22 4)；(2) x- 4x+3)2=(X-8、方程x+m 2=n的根是9、当 x=-1 满足方程 x2-2 ( a

47、+1) 2x-9=0 时，a=10、：方程m+1 x2m+1+ m-3 x-1= 0，试问:1 m取何值时，方程是关于 X的一元二次方程，求出此时方程的解;2m取何值时，方程是关于 X的一元一次方程 11、关于x的一元二次方程a+1 x2+3x+a2-3a-4=0的一个根为0,那么a的值为A、 -1 B 、 4 C 、 -1 或 4 D12、不管X、y为什么实数，代数式x2+y2+2x-4y+7的值§ 2、2用公式法求解一元二次方程一. 教学目标：1、能够熟练地、灵活的应用配方法解一元二次方程。2、进一步体会转化的数学思想方法来解决实际问题。3、培养观察能力运用所学旧知识解决新问题。

48、二. 教学重点、难点：能够熟练的应用配方法解一元二次方程和两种方法的选用。用求根公式解简单数字系数的一元二次方程。对求根公式的推 导过程的理解三. 概念：1. 公式法：公式法是用求根公式解一元二次方程的解的方法，它是解一元二次方 程的一般方法。i2. 兀二次方程 ax2 bx c 0(a 0)的求根公式：x b (b2 4ac 0)2a四. 教学程序：一、复习：上节课我们学过的解一元二次方程的根本思路是什么？其关键是什么？二、新授：1、例题讲析：例1 利用公式法解方程x2-7x-18=0分析：此方程中哪些数字相当于 ax2+bx+c=0 (a 0)中的a、b、c?试写出解 方程的完整过程。例2

49、对于问题：k取何值时，kx 2+3x+4=0有两个不相等的实数根，下面的解法是否正确？假设不正确，请给出正确解法解：=3-4 k 4=9-16k令 9-16k >0，那么 k< 16即当k< 时，方程kx2+3x+4=0有两个不相等的实数根。162、用公式法解一元二次方程 的步骤：(1) 把方程化为(一般形式)(2) 写出一元二次方程的各项(系数)(3) 计算( 判别式bA2-4ac )的值，并判断出与(0)的大小关系(4) 在一元二次方程 有(bA2-4ac >=0 )的前提下，用公式( x= (-b+(- ) ")/2a )求出x的值(5) 具体写出 x1

50、= ("+“) /2a ) x2= (-b- ") /2a)3、利用配方法推导一元二次方程的求根公式假设给出一个一元二次方程ax2+bx+c=0( a 0)你觉得应如何利用配方法求解？(1) ax2+bx+c=0 (a0)方程的两边同时除以 a可得到： 。(2) 把上式中的常数项移项可得： (3) 如果对上式进行配方，方程两边应加上什么式子，这个式子是怎样得到的？(4) 配方后可得： 。(5) 思考：对于上式能不能直接利用直接幵平方，为什么？结论：对于一元二次方程 ax2+bx+c=0 (az 0)，当时，它的根是：x=。式子称为求根公式，用解一元二次方程的方法称为公式法。

51、三、作业：1、用公式法解以下方程:2(1) 2x -4x-1=0;2(2) 5x+2=3x;(3)(x-2)(3x-5)=1(4) x2-2x-4=0(5) 5x2=4-2x(6)(x-2)(3x-5)=1(7) x2- 5 2x+8=0(8) x2+2x-35=0(9)25x-15x-10=02(10)9x +6x+1=02(11)16x+8x=32、一个直角三角形三边的长为三个连续的偶数，求这个三角形的三条边长。3、方程m+1xlm|+1+m-3x-1=0.1m取何值时，方程是一元一次方程2m取何值时，方程是一元二次方程，并求出此方程的解。4、x=-2是方程2x +mx-4=0的一个根，那

52、么 m的值是。5、 两个连续奇数的积是 483,那么这两个奇数分别是 、o6、假设一个等腰三角形三边长均满足方程x2-6x +8=0，那么此三角形的周长为o7、一元二次方程有一个根是2，那么这个方程可以是 填上你认为正确的一个方程即可。8、填空:(1)方程x2+2x+1=0的根为xi=，X2二，贝y X1+X2二；x1?X2=(2)方程x2-3x-1=0的根为xi=，X2二，贝y X1+X2二；X1 ?X2=(3)方程 3x2+4x-7=0 的根为 xi=，X2二 _，贝 y X1+X2二；X1?X2 =§ 2、2用分解因式法求解一元二次方程、教学目标:1、了解分解因式法的概念；2、会用因式分解法解某些简单的数字系数的一元二次方程。3、体验解决问题的方法的多样性，灵活选择方程的解法。4、在学习活动中获得成功的体验，建立学好数学的信心。二、教学重点、难点：会用因式分解法解某些简单的数字系数的一元二次方程。 会用因式分解法解某些简单的数字系数的一元二次方程。三、概念：因式分解法：一元二次方程的一边另一边易于分解成两个一次因式的 乘积时使用此方法。四、教学程序：一、复习：1、有两个数a b