第三章 2 岩石的破坏准则

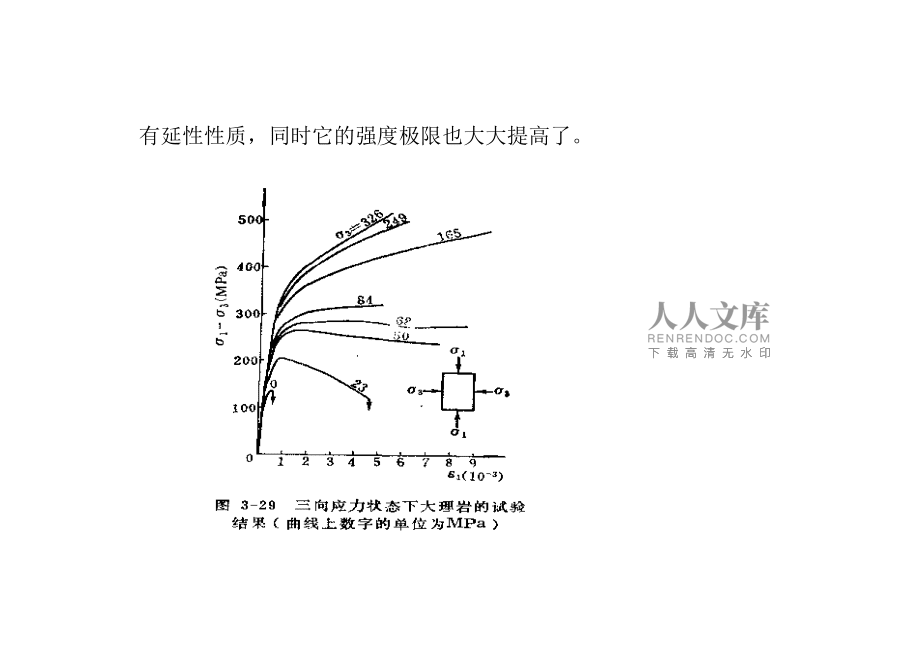
1、五、岩石的破坏准则对岩石试样的室内及现场试验，可获得岩石试样的强度指标，但对复杂应力状态下的天然岩体，又是如何判断其破坏呢？因此，就必须建立判断岩石破坏的准则（或称强度理论）。岩石的应力、应变增长到一定程度，岩石将发生破坏。用来表征岩石破坏条件的函数称为岩石的破坏准则。岩石在外力作用下常常处于复杂的应力状态，许多试验指出，岩石的强度及其在荷载作用下的性状与岩石的应力状态有着很大的关系。在单向应力状态下表现出脆性的岩石，在三向应力状态下具有延性性质，同时它的强度极限也大大提高了。 许多部门和学者从不同角度提出不同的破坏准则，目前岩石破坏准则主要有：最大正应力理论最大正应变理论最大剪应力理论（H.

2、Tresca）八面体应力理论莫尔理论及库伦准则格里菲思理论（Griffith）伦特堡理论（Lundborg）经验破坏准则1、最大正应力理论这是较早的一种理论，该理论认为岩石的破坏只取决于绝对值最大的正应力。即岩石内的三个主应力中只要有一个达到单轴抗压或抗拉强度时，材料就破坏。或适用条件： 单向应力状态。对复杂应力状态不适用。写成解析式： 破坏2、最大正应变理论该理论认为岩石的破坏取决于最大正应变，即岩石内任一方向的正应变达到单向压缩或拉伸时的破坏数值时，岩石就发生破坏。则破坏准则为式中岩石内发生的最大应变值；单向拉、压时极限应变值；这一破坏准则的解析式为（由广义虎克定律） R Rt或Rc推出：

3、破坏实验指出，该理论与脆性材料实验值大致符合，对塑性材料不适用。3、最大剪应力理论（H.Tresca）该理论认为岩石材料的破坏取决于最大剪应力，即当最大剪应力达到单向压缩或拉伸时的危险值时，材料达到破坏极限状态。其破坏准则为：在复杂应力状态下，最大剪应力单位拉伸或压缩时，最大剪应力的危险值则有 或写成 破坏稳定这个理论适用于塑性岩石，不适用于脆性岩石。该理论未考虑中间主应力的影响。4、八面体剪应力理论（Von.Mises）该理论认为岩石达到危险状态取决于八面体剪应力。其破坏准则为 已知单元体三个主应力，取坐标系平行于主应力。作一等倾面（其法线N与三个坐标轴夹角相同）。八个象限的等倾面构成一个封

4、闭的正八面体，此八面体上剪应力和法向应力即为八面体应力。为研究等倾面上的应力，取一由等倾面与三个主应力面围成的四面体来研究。N与x、y、z的夹角分别为，且。设：，则有设等倾面ABC面积为S，则三个主应力面(，面)的面积分别为根据力的平衡条件 , , 推出：，而 等倾面S上合力：所以：另，等倾面S上的法向应力为各分力px、py、pz在N上的投影之和，即这样，等倾面上的剪应力为考虑单向受力时，只有一个主应力不为零，设为R，则代入上式有，推出：适用条件：塑性，5、莫尔理论及莫尔库伦准则该理论是目前应用最多的一种强度理论。该理论假设，岩石内某一点的破坏主要取决于它的大主应力和小主应力，即1和3，而与中

5、间主应力无关。也就是说，当岩石中某一平面上的剪应力超过该面上的极限剪应力值时，岩石破坏。而这一极限剪应力值，又是作用在该面上法向压应力的函数，即。这样，我们就可以根据不同的1、3绘制莫尔应力图。每个莫尔圆都表示达到破坏极限时应力状态。一系列莫尔圆的包线即为强度曲线由此可知，材料的破坏与否，一方面与材料内的剪应力有关，同时也与正应力有关关于包络线：抛物线：软弱岩石双曲线或摆线：坚硬岩石直线：当10MPa 时为简化计算，岩石力学中大多采用直线形式：c凝聚力（MPa） j内摩擦角。该方程称为库伦定律，所以上述方法合称为：莫尔库伦准则。当岩石中任一平面上 时，即发生破坏。即： 下面介绍用主应力来表示莫

6、尔库仑准则。任一平面上的应力状态可按下式计算 a最大主应力面（s1）与滑动面夹角。根据莫尔应力圆，可建立任一滑动面的抗剪强度指标与主应力之间关系。1）c和j值与s1、s3和a角关系在s1s3的应力圆上，找出2a的应力点T（TM为半径为）则，与直径TM垂直且与圆相切的直线即为 根据几何关系，得出 代入中，得到 另由公式推导：将s1、s3表示的 s 和 t 代入中，导出或对求导， 推出：破坏面与最大主应力面的夹角 而与最大主应力方向的夹角 2）用主应力s1、s3表达的强度准则将 s 和 t 的表达式代入 中， 利用关系： 化简得： 当s3=0时（单轴压缩）：，令，则，当s1=0时（单轴抗拉）：该值

7、为 直线在s轴上的截距，但与实测的Rt有差别，需对s0时的直线段进行修正。 岩石破坏的判断条件： ， 破坏， 极限，稳定6、格里菲思（Griffith）理论以上各理论都是把材料看作为连续的均匀介质，格里菲思则认为：当岩石中存在许多细微裂隙，在力的作用下，在缝端产生应力集中，岩石的破坏往往从缝端开始，裂缝扩展，最后导致破坏。在岩石中任取一条裂隙，其长轴与s1方向成b角。格里菲思假定，裂隙是张开的，且形状接近于椭圆，一旦拉应力超过岩石的局部抗拉强度，在张裂隙的边壁就开始破裂。1）.任一裂隙的应力。假定：椭圆可作为半元限弹性介质中的单个孔洞处理，二维问题处理，取椭圆参数方程：，椭圆的轴比为：椭圆裂隙

8、周壁上偏心角的的任意点的切向应力 可用弹性力学中英格里斯（Inglis）公式表示：由于裂缝很窄，轴比很小，形状扁平，所以最大应力显然发生在靠近椭圆裂隙的端部，即很小的部位，当时，又由于m，很小，略去高次项，则有 m为定值，当，确定时，、也为定值，则仅随而变。这是任一条裂隙沿其周边的切向应力。显然在椭圆周边上，随不同有不同的值，对求导。 推出：则，最大切向应力 2）岩块中的最大切向应力所在的裂隙上面导出了某一条裂隙上的最大切向应力，但在多条裂隙中，哪一条裂隙的 最大？，与，的关系为： ， 代入 中，显然与有关，对其求导，便可求得为最大的那条裂隙，即确定出角。 即取 则， ，有0或代入中，0时，

9、或 0时，或0。共四个可能极值，与1平行或垂直的裂隙。将 代入 中，共有两个极值，即与1斜交裂隙中有两个方向裂隙的切向应力达极值。 因为0或时，或1。因此，与1斜交时，必须0或， 即 时 才是与1斜交，则要求 或 此时，裂隙的最大拉应力为 （*）如果， 则 ，则必为负值（拉应力）此时由推出，即为0或90°，表明裂隙与1平行或正交。因为，考查0，的极值，则 （*）为最大拉应力。式（*）（*）即为岩石中的达到某一临界值时就会产生破坏。为了确定m值，做单轴抗拉试验，使3垂直裂隙面（椭圆长轴），则这时的 推出 这说明裂隙边壁最大应力与m乘积必须满足的关系。此时，格菲思强度理论的破坏准则为：I

10、. 由（*）式，当时， 则 ， II. 由（*）式，当时，代入 ，则有：等于0，处于极限状态；大于0， 破坏；小于0， 稳定。上面的准则是用1、3表示的，也可用，表示将 代入 中，推出：， 显然与莫尔圆的色线接近，在时的包线更接近实际。7、修正的格里菲思理论格里菲思理论是以张开裂隙为前提的，如果压应力占优势时裂隙会发生闭合，压力会从裂隙一边壁传递到另一边，从而缝面间将产生摩擦，这种情况下，裂隙的发展就与张开裂隙的情况不同。麦克林托克（Meclintock）考虑了这一影响，对格里菲思理论进行了修正。麦克林托克认为，在压缩应力场中，当裂缝在压应力作用下闭合时，闭合后的裂缝在全长上均匀接触，并能传递

11、正应力和剪应力。由于均匀闭合，正应力在裂纹端部不产生应力集中，只有剪应力才能引起缝端的应力集中。这样，可假定裂纹面在二向应力条件下，裂纹面呈纯剪破坏。其强度曲线如图。由图可知OCBD=（半径）OD=（圆心）EB=， OE=,ED=OD-OE=-AB=EB由 AB=BD-AD，可推出式中，摩擦系数另外，按格里菲思理论，推出取为，裂隙面上的压应力，则有当很小时，取0时（勃雷斯Brace）当时<0时（拉应力），上两式不适用。低应力时，格里菲思与修正的格里菲思理论较为接近，高应力时差别大（当3>0时）。8、伦特堡（Lundborg）理论伦特堡根据大量的岩石强度试验认为，当岩石内的正应力达到

12、一定限度，即相应于岩石的晶体强度时，由于晶体破坏，继续增加法向荷载就不再增大抗剪强度。用下式来描述岩石在荷载下的破坏状态：，研究点的正应力和剪应力（MPa）当没有正应力时（=0）岩石的抗切强度（MPa）岩石晶体的极限抗切强度（MPa）A系数，与岩石种类有关。当岩石内的剪应力和正应力达到上述关系时，岩石就发生破坏。式中的实际上是代表最大的剪应力，因而是强度。上式中的,A由试验确定，见P55表3-5。9、经验破坏准则现行的破坏理论并不能全面的解释岩石的破坏性态，只能对某一方面的岩石性态做出合理的解释，但对其它方面就解释不通。因此，许多研究者在探求经验准则，目前应用较多的经验破坏准则为霍克（Hoke）和布朗（Brown）经验破坏准则。 Hoke和Brown发现，大多数岩石材料（完整岩块）的三轴压缩试验破坏时的主应力之间可用下列方程式描述： Rc完整岩石单轴抗压强度（MPa）；m与岩石类型有关的系数m值是根据岩石的完整程度，结晶及胶结情况，通过大量试验结果及经验而确定的。岩石完整、结晶或胶结好，m值就越大，最大的为25。 对于岩体，Hoke