数独方法及技巧(小图)

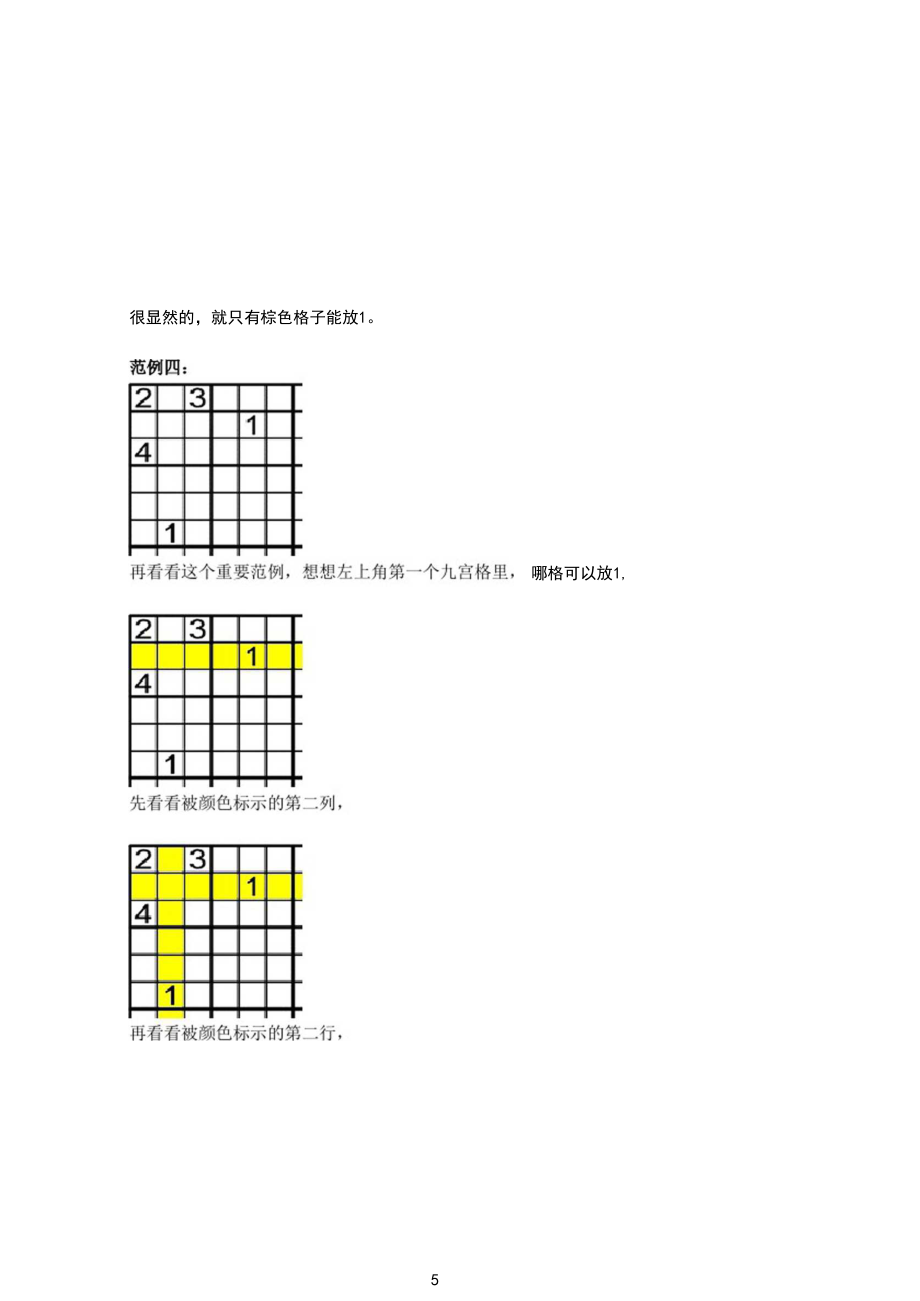
1、创作编号上GB8878185555334563BT9125XW创作者：凤呜大王*数独技巧（SudokuStrategies)数独快速入门（上篇） 数独快速入门（中篇） 数独快速入门（下篇）数独快速入门（上篇）在左边第一个九宫格里，哪格可以放数字1,先看到再第一列和第二列里已经有了数字1,上面两列格子已经不能放1 了,范例二:2的旁边似乎都可以放1的样子,范例三:13看被颜色标示的第二行与第三行，又是不能放1,很显然的，就只有棕色格子能放1。哪格可以放1,经过分析后可知1要放在这棕色格子。数独快速入门（中篇）看看这个比上篇难的，想想1能放在哪里呢,哪一格,可以先看看邻近的九宫格，发现到棕色格子能

2、放1喔,这时候就不用怀疑马上写下10看看这个有技术性的，想想1能放在哪里,2 3 4 5 6111I看到黄色的第一列已经有1,所以不能再放1了,就中央的九宫格而言，合理的推论，1一定是在第二既然知道第二列的情况，再考虑黄色区域后,那么可以先确定右方九宫格的1必然放在这棕色格能否决定1的位置,由上篇的概念再进阶，考虑这上面三个九宫格，看看23456789再考虑到第一行黄色区域，看到有8和9 ,这下就可确定1绝对放在左上角的棕色格子。数独快速入门（下篇）再看到第一列和第三列的黄色区域，这黄色区域里已在左上九宫格里，能放1的只有红色与棕色格子，但红色格子将会被2和3所占据，所以能确定棕色格子必然为1

3、。下1、8、9可以填，然后，又看到第一行有8和9,所以，棕色格子必然不会是8 和9,那么，就只剩下1可以填入啦！ 直观法(Direct Elimination Techniques) 候选数法(Candidates Elimination Techniques)直观法(Direct El i mi nation Techniques)经常在报章杂志上看到的数独谜题，一般就算再难都可以用直观法来解决。它不 需要象候选数法(Candidates Elimination Techniques)那样在每个空白的单元格中 用铅笔填上一大堆候选数。你只要有相对锐利的眼光和一定的逻辑分析能力，就可以 准确地

4、把空余的数字逐个填出来。实际上，直观法就是对数独游戏规则的充分利用。 虽然它并不如候选数法(Candidates Elimination Techniques)那样强大，但通常要 想体会解决数独谜题的乐趣，使用直观法却是不二之选。直观法(Direct El imination Techniques)具有以下的特点：轻松上手。即便是数独新手，在拿到谜题的一刹那，就可以用直观法来解题了。无需辅助。在纸上解题时一般只需要一支钢笔就可以。因为是通过推理和逻辑 分析来确定哪个格填哪个数，或是哪个数填在哪个格里，所以基本不需要猜测。容易掌握。对于直观法(Direct Elimination Techniq

5、ues)中应用的各种算法， 可以很快掌握并应用于实际中。相对简单。比起候选数法(Candidates Elimination Techniques),它的算法相 对比较简单，当然能解决的谜题的复杂度也相对要低。在直观法(Direct EI imination Techniques)中，常用的算法包括：1 .单元唯一法(Sole Position Technique )2 .单元排除法 (Basic Elimination Technique )3 .区块排除法(Block Elimination Technique )4 .唯一余数法(Sole Number Technique )5 .组合排

6、除法 (Combination Elimination Technique)6 .矩形排除法 (Rectangle Elimination Technique)1 .单元唯一法(Sole Position Technique )这应该算是直观法中最简单的方法了。基本上只需要看谜题，推理分析一概都用 不上，这是因为要使用它所需满足的条件十分明显。同样，也正是因为它简单，所以 只能处理很简单的谜题，或是在处理较复杂谜题的后期才用得上。我们先来看一个例子:123456789在上图中，观察行B,可以看到除了 B3外，其他所有的单元格中都已有了数字, 根据数独游戏的规则，即每行，列或区块中不能有重复的数

7、字，则B3中能填入的数 字只能是行B中所未出现过的，也就是数字3。所以可以毫不犹豫地在B3中填入3。这就是单元唯一法在行中的应用。这里的单元(Unit, or group),指的是行，列 或区块。所以有三种情况：当某行有8个单元格中已有数字，或当某列有8个单元格中已有数字，或当某区块有8个单元格中已有数字。无论是哪种情况，我们都可以很快地在该行，列或区块剩余的空格中填入该单元 还未出现过的数字。下面是单元唯一法在列中的应用:BC DE F51642267391819267263196149729276642712571693184327596在第7列中，只有F7未填入数字，且这一列中数字8还未

8、出现过。所以F7二 8。在区块中也是一样:GB8878185555334563BT9125XW创作编号工创作者：凤呜大王*198193763159824913875617856423938914754972368123168381123456789A B C D在起始于D7的区块中，只有E7还未填入数字，且这个区块中数字5还未出现 过，所以可以马上在E7中填入5。单元唯一法在解题初期应用的几率并不高，而在解题后期，随着越来越多的单元 格填上了数字，使得应用这一方法的条件也逐渐得以满足。2 .单元排除法(Basic El imination Technique )单元排除法是直观法中最常用的方法

9、，也是在平常解决数独谜题时使用最频繁的 方法。使用得当的话，甚至可以单独处理中等难度的谜题。使用单元排除法的目的就是要在某一单元(即行，列或区块)中找到能填入某一 数字的唯一位置,换句话说，就是把单元中其他的空白位置都排除掉。它对应于候选 数法中的隐式唯一法。那么要如何排除其余的空格呢？当然还是不能忘了游戏规则，即行，列或区块中 不能有重复的数字。从另一个角度来理解，就是如果某行中已经有了某一数字，则该行中的其他位置不可能再出现这一数字。如果某列中已经有了某一数字，则该列中的其他位置不可能再出现这一数字。如果某区块中已经有了某一数字，则该区块中的其他位置不可能再出现这一数 字。单纯理解上面的规

10、则还是不足以解题，但是在实践中这些规则却可以交叉使用。 在实际解题过程中，应用最多也最方便的是对区块的单元排除法，我们可以先看下而 这个例子：123456789876934251192765438453218976XXX2892834X38562732599632对于起始于D1的区块，其未填数字的空格有6个之多，如果不使用单元排除法, 是很难为这一区块填入任何数字的。这时我们就可以利用行，列及区块的相互关系， 即一个单元格既在某一行上，也同时在某一列上以及某一区块中的这种关系来解题。观察数字9在谜题中的位置,可以看到它出现在32, A4, C7, D8, II 和H9。而这些位置中,只有B2,

11、 D8和口与起始于D1的区块有关联。因为 口:9,它所在的第1列上的其他单元格中不可能再出现9,而区块中的D1和F1 正好也在第1列上，所以这两个单元格填入9的可能性被排除。同理，因为B2=9, 它所在的第2列中的其他单元格不可能再填入9,而区块中的D2和E2也正好在第 2列上，因此，这两个单元格填入9的可能性也被排除掉了。再看行D,因为D8”9, 所以该行上的EDI, D2和D3也不可能再填入9,而这些单元格正好也在起始于EDI 的区块中。所以，这个区块中能填入数字9的位置就只剩下了 E3,这样就通过排除 法找到了答案，即E3=9。下而再看一个在行中使用单元排除法的例子：在谜题中观察数字4和

12、行H,在行H有5个空单元格无法确定数字，但是C3位 置上的4使得其所在的第3列中的其他单元格上不能再出现4,所以H3不能填入4。 口4上的4使得其所在的区块中也不能再填入4,它帮助行H排除了两个单元格H4 和H6,而第8列上的E8中的数字4使得同样位于这一列上的H8也排除了填入4 的可能。这样，行H中能填入4的位置就只剩下H9 了。在列中也可以使用单元排除法:12345678982712X32828719187469517X2539343795在第7列中，我们试图确定能填入数字1的位置°在行B中，数字1已经出现在 B2±,所以B7不可能再填入数字1 了。而位于D8的数字1也

13、使得F7排除了填 入数字1的可能，因为它们位于同一区块中。这样，第7列上就只有A7能填入数字 1 了。通过上面的示例，可以看到，要对区块使用单元排除法，需要观察与该区块相交 的行和列。要对行使用单元排除法，需要观察与该行相交的区块和列。要对列使用单 元排除法，需要观察与该列相交的区块和行。在实际解题过程中，行，列和区块之间的关系并不象上面这些图中所示的那么明 显，所以需要一定的眼力和细心观察。一般来说，先看哪个数字在谜题中出现得最多, 就从哪个数字开始下手，找到还未填入这个数字的单元(行，列或区块)，利用已填 入该数字的单元格与单元之间的关系，看能不能排除一些不可能填入该数字的位置， 直到剩下

14、唯一的位置。如果害怕搞不清已经处理过哪些数字的话，可以从数字1开始, 从左上角的区块开始一直检查到右下角的区块，看能不能在这些区块中应用单元排除 法。然后测试数字2,以此类推。单元排除法是应用得最多的直观法，虽然在实践中经常会因为粗心而漏掉很多使 用这一方法的机会，但只要勤加练习，就可以运用自如。3 .区块排除法(Block El imination Technique )区块排除法是直观法中进阶的技法。虽然它的应用范围不如单元排除法那样广 泛，但用它可能找到用单元排除法无法找到的解。有时在遇到困难无法继续时，只要 用一次区块排除法，接下去解题就会势如破竹了。区块排除法实际上是利用区块与行或列

15、之间的关系来实现的，这一点与单元排除 法颇为相似。然而，它实际上是一种模糊排除法，也就是说，它并不象单元排除法那 样利用谜题中现有的确定数字对行，列或区块进行排除，而是在不确定数字的具体位 置的情况下进行排除的。这句话听起来似乎不好理解，让我们先从一个例子入手，看 看区块排除法是怎么应用的。123456789A B C D E F38715895318129868398249583618357649835对于上面这个谜题，用基本的单元排除法或是单元唯一法都无法再找到解。这时 可以尝试使用区块排除法。我们先从填入数字最多的区块着手，也就是起始于G4的区块，该区块中只有H6 和15为空，且剩余数字

16、1和2还未填入。这样，我们可以想办法确定这两个数字的 位置。观察全局，可以看到D2=2,根据单元排除法，它所在的第2列上不能再出现数 字2,所以H2和12将不能填入2,这使得起始于G1的区块中数字2可能出现的 位置仅剩下口和13,见下图:12345678938715895318129868398249583618X35762?X2?49835虽然我们无法确定2在起始于G1的区块中的确定位置，但幸运的是，能填入2 的位置正好都在行I上，也就是说，无论2在口还是在13,行I的其他单元格中 将不可能再出现数字2,所以可以亳不犹豫地排除在15填入2的可能性，这样，对 于起始于G4的区块而言，能填入数字

17、2的位置就只剩下H6 了。所以H6=20接下 来，当然亳无疑问，利用单元唯一法，在15填入数字1。先小结一下上而的求解方法：解题时，实际上是在对目标区块（主区块）有影响 的区块（辅助区块）中应用单元单元排除法，使辅助区块满足某些条件并能参与对主 区块的数字排除。实际应用中，可能出现下面四种情况：'彳某数字在某个区块中可填入的位置正好都在同一行上，因为该区块中必须要有 该数字，所以这一行中不在该区块内的单元格上将不能再出现该数字。当某数字在某个区块中可填入的位置正好都在同一列匕因为该区块中必须要有 该数字，所以这一列中不在该区块内的单元格上将不能再出现该数字。邙某数字在某行中可填入的位置

18、正好都在同一区块上，因为该行中必须要有该数 字，所以该区块中不在该行内的单元格上将不能再出现该数字。当某数字在某列中可填入的位置正好都在同一区块上，因为该列中必须要有该数 字，所以该区块中不在该列内的单元格上将不能再出现该数字。其中1, 2两种情况相对常见，也比较容易判断。上面的示例就是第1种情况。下而我们会看到第2种情况的例子：123456789虽然在起始于A7的区块中，未填入数字的空单元格多达4个，但我们还是可以 轻松地确定数字5的位置。这是因为在起始于G7的区块中，我们欣喜地发现数字5 可能出现的位置正好都在第8列上，这时5的确切位置已经不重要了，因为它已经满 足了上面介绍的第2种情况的

19、条件，因此可以参与对起始于A7的区块进行数字排除 了。在它的影响下，A8和B8中填入数字5的可能性已经不存在，因为它们都在第 8列上。这样，在起始于A7的区块中，数字5能填入的位置只剩下A9和C9 了。 这时，我们再利用单元排除法，通过R4位置上的数字5再消除其所在行A上的A9, 最终得到能填入5的唯一位置C9。下而看几个比较少见的例子12345678971242ZX3?3?46574XXX781264257927458136372268362912476在行C上，数字3的位置可以通过下面的方法来确定：先看行B,利用单元排除法，通过H2和F3位置上的3进行列排除，得到行B 中能填入3的位置为B

20、4和B5。碰巧的是，这两个单元格都在起始于A4的区块中, 这时已经满足了上述情况3的条件。利用单元排除法的区块排除，则行C上的C4和 C5都不能再填入3：再加上F3的列排除的共同努力，最终确定数字3在行C上的唯一位置就是Cl 0第4种情况的例子如下:12345678961755374:91148X375768?3X11475638?1X7945379127514633142587在这个示例中，只是使用单元排除法和单元唯一法到这一步就继续不下去了。要 想求得数字8在第6列的位置，就必须要借助区块排除法。先看第4列，通过位于C3 和18的数字8的行排除，使8在第4列可能填入的位置只剩下D4和F4,

21、而这两 个单元格正好都在起始于D4的区块中。因为第4列不能没有数字8,而数字8如果 填在区块中的其他位置（如D6, E6或F6）时将迫使D4和F4上不能再填入8, 这样会导致第4列没有数字8。因此,第6列中的D6,没6和F6能填入数字8的 可能性被排除。这样第6列中就只剩下B6能填入8 了。实际解题过程中，还会碰到比较复杂的情况，看下面的谜题:12345678964172215139283412768137413577946你能确定数字3在起始于A1的区块中的位置吗？先看位于C5的数字3,它不 仅排除了同一行中C1和C3中填入3的可能性，也同时排除了同一行中C8和C923填入3的可能性，这使得

22、在起始于A7的区块中，能填入3的位置只剩下B8和B9, 见下图：67Ux64172X2153?3?1X39XXX 28341 3?X276 3?X8137413577 946利用区块排除法,在起始于区7的区块中,无论3在区8还是法9,行B中的其 他位置都不能再填入3,所以置1, B2和入3都被排除。于是,在起始于A1的区 块中，能填入3的位置仅剩下A1和A2 了。但至此我们还无法确定3的准确位置， 这时我们还要借助于其他的辅助区块来进一步排除。123456789A B C D观察起始于D1的区块，利用D7位置上的3排除同一行的D1,以及用G3位 置上的3排除同一列的E3和F3,使区块中可能填入

23、3的位置只余E2和F2,刚 好这两个位置都在第2列中，符合上而介绍的第2种情况，于是可以把A2也排除掉。 最后，我们就可以很肯定地在A1中填入数字3 了。这个例子同时使用了多个辅助区块同时参与排除。在实际使用中虽然这种情况并 不常见，但却也不少见。关犍在于如何能正确识别并恰当应用区块排除法、相信通过 大量的练习并勤于分析思考，这种方法就可以运用自如，得心应手。F而是其他的一些例子，可以帮助更好地理解并掌握这种技法:12345678916734672169一534172X68613592479?29?846X583659?126139?851579?36123456789647XX2343?2X

24、513485192443684X823?53?XXX3847128123456789GB8878185555334563BT9125XW创作编号上创作者：凤呜大王*398546181?X4953451?93827534892193584845139X1?1?95X348X583496943X8254 .唯一余数法(Sole Number Technique )唯一余数法是直观法中较不常用的方法。虽然它很容易被理解，所以说明这个方 法不需要很大篇辐，然而在实践中，却不易看出能够使用这个方法的条件是否得以满 足，从而使这个方法的应用受到限制。与单元唯一法相比，唯一余数法是确定某个单元格能填什么数的

25、方法，而单元唯一法 是确定某个数能填在哪个单元格的方法。另外，应用单元唯一法的条件十分简单，几 乎一目了然。与候选数法相比，唯一余数法相当于显式唯一法。虽然显式唯一法是候选数法中 最简单且应用最容易的方法，但在直观法中却正好相反。先看一个例子：2345678978248637594728785891577981769538587314936428751对于单元格G9应该填入什么数字，就算你把前面介绍的所有直观技法都用上， 也不得而知。然而，我们通过观察它所在的行，列和区块，可以发现除了数字2以外, 1到9中其他的数字都出现了，其中行G中包含了 7, 6, 9, 5, 3和8,第9列中包 含了数

26、字5, 8, 7和1,起始于G7的单元格中包含了 3, 8, 4, 7, 5和1。这样， 如果G9不填入数字2,就一定会违反游戏“行，列或区块不能出现重复数字”的规 则。所以G9中的数字一定是2总结一下，就是如果某一单元格所在的行，列及区块中共出现了 8个不同的数字, 那么该单元格可以确定地填入还未出现过的数字。怎么样，很简单吧，但在实践中却不那么容易识别。看下面的谜题：12345678971258431252348387613482895646843262789你能看出来对哪个单元格应用唯一余数法吗?还有这个谜题:234567894657216575817926588265197258674

27、3876521答案分别是E6=9和案7=9。一般来说，只有在使用基本的排除方法都失效的情况下，才试着使用这个方法来 解题。5 .组合排除法(Combination EI imination Technique)组合排除法和区块排除法一样，都是直观法中进阶的技法，但它的应用范围要更 小一点。一般情况下，基本没有机会用到这种方法解题，所以要找到相应的例子也都 很困难。当然，如果你希望优先以这个技法来解题的话，还是能碰到很多能符合使用 组合排除法条件的情况。组合排除法，顾名思义，要考虑到某种组合。这里的组合既包括区块与区块的组 合，也包括单元格与单元格的组合，利用组合的关联与排斥的关系而进行某种排除

28、。 它也是一种模糊排除法，同样是在不确定数字的具体位置的情况下进行排除的。下面 先看一个例子：对于上面这个谜题，你能确定数字6在起始于G4的区块中的位置吗？要想获得正确的答案初看起来有些困难。因为虽然在G9和H3已经存在了两个 6,但是利用它们只能行排除区块中的G4和H6两个单元格，还是无法确定6到底 是在14还是在15中。这时候，组合排除法就派上用场了。现在撇开起始于G4的区块，先看它上面的两个区块，即起始于A4和D4的区 块。这几个区块的共同特点是占有同样的几列，也就是第4列至第6列，因此它们之 间的数字会相互直接影响。对于起始于A4的区块，利用81处已有的数字6进行行排除，可以得到这个区

29、 块中可能填入6的位置只剩下两个：B5和C6。对于起始于D4的区块，利用E7 处已有的数字6进行行排除，可以得到这个区块中可能填入6的位置也剩下两个：F5 和F6。这时，我们仍无法确定6在这两个区块中的确切位置。但不妨对可能出现的情况 作一下分析：假设在起始于始4的区块中，B5=6,则同一区块中的于6必不为6,而且B5还将列排除F5,这样在起始于D4的区块中，只有F6k6c假设在起始于A4的区块中，C6=6,则同一区块中的B5必不为6,而且C6 还将列排除F6,这样在起始于D4的区块中，只有F5= 6c简单地说,只有两种可能:B5=6且卬6=6,或者筒6=6且F5=6。决不会再 出现其他的情况

30、。但无论是其中哪一种情况，第5列和第6列都会有确定的6出现在 这两个区块中，也就是说，第5列和第6列的其他位置不可能再出现数字6。这样， 原本无法肯定的6在起始于G4区块中的位置，一下子就变得明确了.1234567896285756?1858936?3651287497X5X61848176?6?5321X75867681X585口271利用起始于A4和D4的区块对起始于G4的区块进行列排除，可以把15排除 掉，这样，就只剩下14可以填入6 了。小结一下，组合排除法的要满足的条件如下：如果在横向并行的两个区块中，某个数字可能填入的位置正好都分别占据相同的 两行，则这两行可以被用来对横向并行的另

31、一区块做行排除。如果在纵向并行的两个区块中，某个数字可能填入的位置正好都分别占据相同的 两列，则这两列可以被用来对纵向并行的另一区块做列排除。让我们再看一个例子:234567894283718417622548324864587824986142586194415926要想确定数字1在起始于D4的单元格中的位置，我们将设法借助于其横向上相 邻两个区块的帮助。123456789A B C D E428371841762254831?21?481?61?X458X1?X7X82X4X986142586194415926利用12的列排除，我们可以把起始于D1的区块中的E2和F2排除掉，这样， 这个区

32、块中能填入1的位置剩下DI, D3和E1L 利用区7的列排除，可以把起 始于D7的区块中的E7和F7排除掉，再利用A9的列排除，可以把这个区块中E9 和F9排除掉，这样，这个区块中能填入1的位置只剩下D8和E8。虽然在起始于D1的区块中，能填入1的位置多达3个，但是它们正好只分布在 行D和行E上，而且在起始于D7的区块中能填入1的位置所占据的也是这两行。最 终1的位置只可能有三种情况：俗1=1且E8=l：或者的3=1且E8=l；或者的1=1 且D8=1。无论是哪种情况，行D和行E都会有确定的1出现在这两个区块中，也就 是说，这两行的其他位置不会再出现1。于是，42837184176225483

33、1?21?481?61?X4X58X1?X7X82X4X986142586194415926123456789ADBc借助于这两个区块的行排除，我们可以把起始于D4的区块中的D4和D6排除 掉，再利用G4位置的列排除，最终确定1的位置在F6。下而是其他一些使用组合排除法的例子：59241374?4?95268X2574984?4?2914?4?922X974X285949625x926ABCD123456789123456789A BCD EF GH19?47274X3292839?59?459326781812X7X9736824579?89?12325XXX98269?5712345678

34、9264194562488912747938264?4?XX1XX49X4?XLL286在实践中，组合排除法的实际应用机会不如区块排除法多。但是，掌握这一技法 无疑可以大大提高求解谜题的灵活性，从而增加解题的乐趣。6 .矩形排除法(Rectang Ie EI i m i nat i on T echn i que)矩形排除法虽然浅显易懂，但一般在实际解题的时候应用得却比较少。这是因为 即使谜题中存在满足使用这一方法的情况，也很难直接看出来。然而，相对组合排除 法而言，在解题过程中倒是能有更多的机会用上矩形排除法。下面先看一个例子：对于这个谜题，如果不用矩形排除法是无法继续下去的。我们将通过讲解

35、这种技 法，从而找到数字8在起始于G1的区块中的位置。乍看之下，好象一筹莫展。因为 B2和E3上的8只能列排除左下角这个区块中的G2, H2, G3和13这4个 单元格，这时仍剩下两个单元格G1和H1无法确定。让我们先来留意一下第6列，这一列中暂时没有8,那么8可能会填入哪几个单 元格中呢?首先，B2中的8行排除了 B6,而E3和F4中的8又分别行排除了 E6 和F6。这样,能填入8的位置就只剩下的6和16 了。见下图：同样，对于第9列，由于F4的行排除，F9不可能填8,所以这一列能填入8 的位置也就只剩下C9和19 了。凑巧的是，这两列中能填入8的位置都在同样的两行上，即行C和行I。这时就

36、为我们应用矩形排除法创造了前提条件。如果第6列中C6=8,那么16和C9一定不能是8。而第9列这时就只剩下19 能填入8 了：又或者如果第6列中口6=8,那么又6和19一定不能是8,而第9列就只剩下C9能填入8 了。不可能再有第3种情况。所以，要么不6=8且19=8,要么16:8且C9=8。但无论是哪种情况，不难发现，行C和行I都已填入了 8,所以这两行的其他位置不 可能再填入8。我们正好可以利用这一点来进行排除。123456789A B C D EF G H观察起始于G1的区块，我们已经知道现在只剩下G1和口两个单元格无法确 定了，通过上面的分析，利用矩形排除法排除位于行I上的II，就可以确

37、定数字8 一定在G1上。总结一下，使用矩形排除法的条件如下：如果一个数字在某两行中能填入的位置正好在同样的两列中，则这两列的其他的 单元格中将不可能再出现这个数字：如果一个数字在某两列中能填入的位置正好在同样的两行中，则这两行的其他的 单元格中将不可能再出现这个数字。让我们再来看一个例子:123456789做到这一步时，不用矩形排除法的话恐怕是走投无路了。这次还是要在起始于G1 的区块中找到数字4的位置。但我们无法确定4究竟在G2还是G3呢？先要找找看有没有满足矩形排除法条件的情况存在。观察行B,在这一行中，由 于C5的区块排除，B4和B5都不能为4,再加上的8列排除了B8,这样行B中 能填入

38、4的位置包括B1和B3。再看行F,由于D6的列排除，使得F6不能填4,所以行F中能填入4的位置 只有F1和F3,GB8878185555334563BT9125XW创作编号上创作者：凤呜大王*幸运的是，行B和行F中能填入4的位置正好都位于同样的两列上，即第1列和 第3列。根据上面矩形排除法的规则，第1列和第3列中不在行B和行F上的单元格 中不能填入4,所以G3不能为4。这样，起始于G1的区块中就只有G2能填入4 了。下而是应用矩形排除法的其他一些例子，希望可以帮助大家快速掌握这种方法：矩形排除法可以说是直观法中最困难的技法，因为当前的谜题即使满足应用这一 方法的条件，也实在太难发现了。一般情况

39、下，尽量先使用其他相对简单的直观法。 如果最后连矩形排除法都用上还是无法解题，你可能就需要尝试候选数删减法了。候选数法(Candidates El imination Techniques)对于解决数独谜题，最常使用的方法就是直观法和候选数法，在谜题相对简单时, 直观法可以取得相当好的效果。但是如果谜题比较复杂，直观法的效果就十分有限， 即使通过试探性填数也不一定能够解题，而这时候选数法却可以很好地发挥作用。在 对数独谜题求解的电脑程序的设计上，候选数法也因为高效易实现而被广泛应用。如果用候选数法来解题，必须首先准备一张如下图所示的候选数栅格表：123456789初始化时，每个单元格中都包含了

40、 1至9所有的数字，它表示该单元格中在解题 时还可以选择填入的数字。很明显，不在候选数中的数字是不能够填入该单元格中的。 如果某一单元格中已填入一个确定的数字，则根据数独游戏的规则，即该单元格所在行，列及区块中都不能再出现这个数字，则该数字应从这些单元格中的候选数字中去 除。对于下面的这个谜题：23456789374143728595516254298529876每填入一个数字时，都要将该单元格中的候选数全部删除，同时扫描其所在行, 列和区块，看它们所覆盖的单元格上的候选数中有无该数字：123456789T| 4 5 6 17 8 54 5 65 6S 94 5 67 8 94 5 67 8

41、94 5 67 C 912 34 5 67 8 91 2 34 5 67 8 91 2 34 f 67 8 91 2 34 5 67 8 92 3f 6S 91 2 34 5 S7 3 J1 2 34 f f7 8 91 2 34 f 67 8 9L 2 34 f 67 B 91 2 34 5 67 8，1 2 34 5 67 8，1 2 34 5 67 8 91 2 34 5 67 8 ?2 35 6 B，1 2 34 5 67 8 J1 2 34 5 G7 3 ?1 2 34 5 67 8 9L 2 34 5 67 3 91 2 34 S 61 2 34 § 61 2 34 5 61 2 34 5 62 35 631 2 34 S i7 6 91 2 34 5 11 2 34 5 6L 2 34 5 67 84 5 67 8 91 2 34 5 6? 8 91 2