培优9一次函数综合类问题四大类

1、一次函数与几何综合（讲义）一、知识点睛1. 一次函数表达式：y=kx+b （k, b为常数，kw0）k是斜率，表示倾斜程度，可以用几何中的坡度（或坡比）来解释.坡面的竖直高度BM即为水平宽度，则与水平宽度的比叫坡度或坡比，如图所示， AM即为竖直高度,k=_AM,b是截距，表示直线与y轴交点的纵坐标.|BM2. 设直线 li： yi=kix+bi,直线 12： y2=k2x+b2,其中 ki,笈士0. 若 ki=k2,且 bib2,则直线 1i/12；若ki k2=-i,则直线1i112.3. 一次函数与几何综合解题思路 从关键点出发，关键点是信息汇聚点，通常是函数图象与几何图形的交点.通过点

2、的坐标 和横平竖直的线段长的互相转化将函数特征与几何特征结合起来进行研究，最后利用函数 特征或几何特征解决问题.二、精讲精练1 .如图，点B, C分别在直线丫=2乂和y=kx上，点A, D是x轴上的两点，已知四边形 ABCD是正方形，则k的值为.2 .如图，直线li交x轴、y轴于A, B两点，OA=m, OB=n,将AAOB绕点。逆时针旋转 90°得到 COD. CD所在直线12与直线li交于点E,则li。若直线li, I2的斜率分别为 ki, k2,则 ki k2=.43 .如图，直线y=-x+ 8父x轴、y轴于A, B两点，线段AB的垂直平分线父x轴于点C, 3交AB于点D,则点

3、C的坐标为:4 .如图，在平面直角坐标系中，函数 y=x的图象l是第一、三象限的角平分线.探索：若点A的坐标为(3, 1),则它关于直线l的对称点A'的坐标为;猜想：若坐标平面内任一点 P的坐标为(m, n),则它关于直线l的对称点P的坐标为应用：已知两点B(-2, -5), C(-1, -3),试在直线l上确定一点Q,使点QU B, C两 点的距离之和最小，则此时点 Q的坐标为:5 .如图，已知直线l: y = -，3x + 73与x轴交于点A,与y轴交于点B,将4AOB沿直线 3l折叠，点O落在点C处，则直线CA的表达式为:6 .如图，四边形ABCD是一张矩形纸片，E是AB上的一点

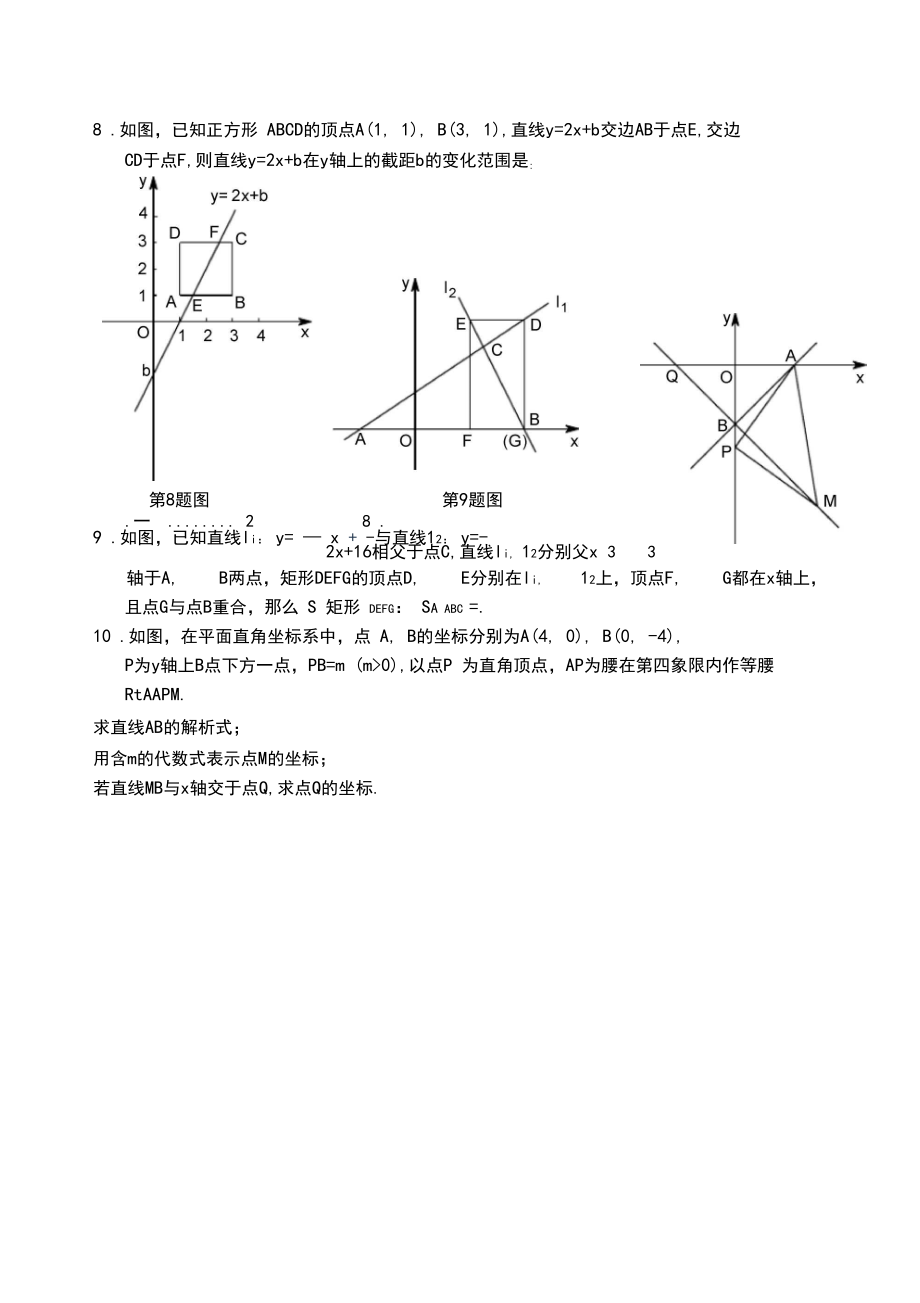
4、，且BE: EA=5: 3, EC=1575,把 BCE沿折痕EC向上翻折，点B恰好落在AD边上的点F处.若以点A为原点，以直线AD为x轴，以直线BA为y轴建立平面直角坐标系，则直线 FC的表达式为7 .如图，矩形 ABCD的边AB在x轴上，AB的中点与原点 O重合，AB=2, AD=1,过定 点Q(0, 2)和动点P(a, 0)的直线与矩形ABCD的边有公共点.(1) a的取值范围是;(2)若设直线PQ为y=kx+2 (kw0),则此时k的取值范围是:8 .如图，已知正方形 ABCD的顶点A(1, 1), B(3, 1),直线y=2x+b交边AB于点E,交边CD于点F,则直线y=2x+b在y

5、轴上的截距b的变化范围是:第8题图第9题图(1)(2)(3).一 28 .9 .如图，已知直线li： y= x + -与直线12： y=-2x+16相父于点C,直线li, 12分别父x 33轴于A, B两点，矩形DEFG的顶点D, E分别在li, 12上，顶点F, G都在x轴上， 且点G与点B重合，那么 S 矩形 DEFG： Sa ABC =.10 .如图，在平面直角坐标系中，点 A, B的坐标分别为A(4, 0), B(0, -4), P为y轴上B点下方一点，PB=m (m>0),以点P 为直角顶点，AP为腰在第四象限内作等腰 RtAAPM.求直线AB的解析式；用含m的代数式表示点M的

6、坐标；若直线MB与x轴交于点Q,求点Q的坐标.一次函数之存在性问题（讲义）一、知识点睛存在性问题：通常是在变化的过程中，根据已知条件，探索某种状态是否存在的题目, 主要考查运动的结果.一次函数背景下解决存在性问题的思考方向：1 .把函数信息（坐标或表达式）转化为几何信息;2 .分析特殊状态的形成因素，画出符合题意的图形；3 .结合图形（基本图形和特殊状态下的图形相结合）的几何特征建立等式来解决问题.二、精讲精练，一一 31.如图，直线y =-手x +点与x轴、y轴分别父于点A,点B,已知点P是第一象限内的 3点，由点P, O, B组成了一个含60°角的直角三角形，则点P的坐标为2.如

7、图，直线y=kx-4与x轴、（1）求点B的坐标和k的值.（2）若点A是第一象限内直线y=kx-4上的一个动点，则当点A运动到什么位置时，4AOB 的面积是6?（3）在（2）成立的情况下，x轴上是否存在一点P,使4POA是等腰三角形？若存在, 求出点P的坐标；若不存在，请说明理由.3 .如图，在平面直角坐标系中，直角梯形 OABC的边OC, OA分别与x轴、y轴重合，AB /OC, /AOC=90°, /BCO=45°, BC= 6" ,点 C 的坐标为(-9, 0).(1)求点B的坐标.(2)若直线BD交y轴于点D,且OD=3,求直线BD的表达式.(3)若点P是(

8、2)中直线BD上的一个动点，是否存在点P,使以O, D, P为顶点的 三角形是等腰三角形？若存在，求出点 P的坐标；若不存在，请说明理由.OB 34 .如图，直线y=kx+3与x轴、y轴分别父于A, B两点，市 ,点C是直线y=kx+3上 与A,B不重合的动点.过点C的另一直线CD与y轴相交于点D,是否存在点C使4BCD 与4AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由.yix15.如图，直线丫=+2与乂轴、y轴分别父于A, B两点，点C的坐标为(-3, 0), P(x,一，1 ,一 ，一y)是直线y =2x +2上的一个动点(点P不与点A重合).(1)在点P的运动过程中，试写出

9、 OPC的面积S与x之 问的函数关系式.27,(2)当点P运动到什么位置时， OPC的面积为一？求出 8此时点P的坐标.(3)过P作AB的垂线与x轴、y轴分别交于E, F两点, 否存在这样的点P,使EOFWBOA?若存在，求出点 的坐标；若不存在，请说明理由.一次函数之动点问题(讲义)一、知识点睛动点问题的特征是速度已知，主要考查运动的过程.1 . 一次函数背景下研究动点问题的思考方向：把函数信息(坐标或表达式)转化为基本图形的信息；分析运动过程，注意状态转折，确定对应的时间范围；画出符合题意的图形，研究几何特征，设计解决方案.2 .解决具体问题时会涉及线段长的表达，需要注意两点：路程即线段长

10、，可根据s=vt直接表达已走路程或未走路程；根据研究几何特征需求进行表达，既要利用动点的运动情况，又要结合基本图形信息.二、精讲精练31 .如图，在平面直角坐标系中，O为坐标原点，直线y = -4X + 3与x轴、y轴分别父于A, B两点点P从点A出发，以每秒1个单位的速度沿射线AO匀速运动，设点P的运动 时间为t秒.(1)求OA, OB的长.(2)过点P与直线AB垂直的直线与y轴交于点E,在点P的运动过程中，是否存在这 样的点P,使EOPWAOB?若存在，请求出t的值；若不存在，请说明理由.2 .如图，直线y=J3x+4Q与x轴、y轴分别交于A, B两点，直线BC与x轴交于点C, / ABC

11、=60° .(1)求直线BC的解析式.(2)若动点P从点A出发沿AC方向向点C运动(点P不与点A, C重合)，同时动 点Q从点C出发沿折线CB-BA向点A运动(点Q不与点A, C重合)，动点P的运 动速度是每秒1个单位长度，动点Q的运动速度是每秒2个单位长度.设 APQ的面 积为S,运动时间为t秒，求S与t之间的函数关系式，并写出自变量t的取值范围.(3)当t=4时，y轴上是否存在一点M,使得以A, Q, M为顶点的三角形为等腰三角 形？若存在，请直接写出点 M的坐标；若不存在，请说明理由.3 .如图，在直角梯形COAB中，OC/AB,以。为原点建立平面直角坐标系，A, B, C 三

12、点的坐标分别为 A(8, 0), B(8, 11), C(0, 5),点D为线段BC的中点.动点P从点 O出发，以每秒1个单位的速度，沿折线OAABBD的路线运动，至点D停止，设 运动时间为t秒.(1)求直线BC的解析式.(2)若动点P在线段OA上运动，当t为何值时，四边形OPDC的面积是梯形COAB 一一，1面积的一？4(3)在动点P的运动过程中，设 OPD的面积为S,求S与t之间的函数关系式，并 写出自变量t的取值范围.4 .如图，直线y = -73x+473与x轴交于点A,与直线y=x交于点P.3(1)求点P的坐标.(2)求AOPA的面积.(3)动点E从原点O出发，以每秒1个单位的速度沿

13、OA方向向终点A运动，过点E 作EF，x轴交线段OP或线段PA于点F, FB，y轴于点B.设运动时间为t秒，矩形 OEFB与AOPA重叠部分的面积为S,求S与t之间的函数关系式.5 .如图，直线l的解析式为y=-x+4,它与x轴、y轴分别交于A, B两点，平行于直线l 的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴、 y轴分别交于M, N两点，设运动时间为t秒(0< t <4).(1)求A, B两点的坐标；(2)用含t的代数式表示 MON的面积S;(3)以MN为对角线作矩形 OMPN,记4MPN和4OAB重叠部分的面积为S2,试探究S2与t之间的函数关系

14、式.如图，满足SdABP=S&ABC的点P都在直线ll , 12上.二、精讲精练1.如图，在平面直角坐标系中，已知 A（-1, 3）, B（3, -2）,则 AOB的面积为:一次函数之面积问题（讲义）一、知识点睛1 .坐标系中处理面积问题，要寻找并利用横平竖直的线,通常有以下三种思路：公式法（规则图形）；割补法（分割求和、补形作差）；转化法（例：同底等高）.2 .坐标系中面积问题的处理方法举例割补求面积（铅垂法）：Sa apb = ahSa apb = ah22转化求面积：2.如图，直线y=-x+4与x轴、y轴分别交于点A,点B,点P的坐标为(-2, 2),则S PAB=第2题图第3题

15、图3.4.交于点C,点D,直线AB与直线CD交于点P.1如图，直线y= x+1经过点A(1, m), B(4, 2若 Sapd=4.5,则 k=n),点C的坐标为(2, 5),求 ABC的面积.5.如图，在平面直角坐标系中，已知 A(2, 4),C(8, 2),求四边形OABC的面积.B(6, 6),如图，直线AB: y=x+1与x轴、y轴分别交于点A,点B,直线CD: y=kx-2与x轴、y轴分别16 .如图，直线y=,x+1与x轴、y轴分别父于A, B两点，C(1, 2),坐标轴上是否存在 点P,使Saabp=&abc?若存在，求出点P的坐标；若不存在，请说明理由.17 .如图，已

16、知直线m的解析式为y = -2x + l,与x轴、y轴分别父于A, B两点，以线段 AB为直角边在第一象限内作等腰 RtAABC,且/ BAC=90°,点P为直线x=1上的动点, 且4ABP的面积与 ABC的面积相等.(1)求 ABC的面积；(2)求点P的坐标.8 .如图，直线PA: y=x+2与x轴、y轴分别交于A, Q两点，直线PB: y=-2x+8与x轴交 于点B.(1)求四边形PQOB的面积.(2)直线PA上是否存在点M,使得4PBM的面积等于四边形PQOB的面积？若存在， 求出点M的坐标；若不存在，请说明理由.OPB【参考答案】1、知识点睛二、精讲精练21. 一32. &#

17、177;, -13. (一3'0),” ,、, 1313、4. (1, 3)； (n, m)；(，)555. 丫 =瓜+3君4_6. y =x +1637. (1) -2<a< 2; (2) k> 1 或 k0 -18. -3<b<-19. 8: 910. (1) y=x-4; (2) M(m+4, -m-8); (3) Q(-4, 0)【参考答案】、知识点睛、精讲精练1. (1,我或(3,6)或(3,乌或(3,W3) 4 44442. (1) B(3, 0), k =一3(2) A(6, 4)(3) P(250)或 P2(- 2屈,0)或 P3(12,0

18、)或P(",0)33. (1) B(-3, 6)(2) y=-x+3(3)p(3,o)或p( V2,3J2)或P3(-3J23+1V2)或P4( 3 3)22222 2,12 6、 , 12 24、4.（=，二）或（一"7，7）或（一4,6）5 55 55. (1)3。 x - 3S 二 43x 34(x < -4)(x-4)179 ,1 9 PL，一浮%】)(3)_ 4 12 一P(£，MP1-5 512 45 5【参考答案】(1)2.(1)OA=4, OB=3;(2) t=1 或 t=7y = - 3x 4、, 3(2)中1 2 * * *S = 2 _ .Ut2 4,3t2(0<t< 4)(4 :二 t :二 8)(3)M1(0,473 8)或乂2(0,4 a +8)或 M3(0, 4 73)3.(1)或 M4(0,y =3x+5(2)4t=32(3)4tS = <_2t +48-2t 48(0 < t < 8) (8<t & 19) (19 ：t < 24)4.(1)(2)P(3,、,3)2.