高中数学_点线面位置关系复习课件201512

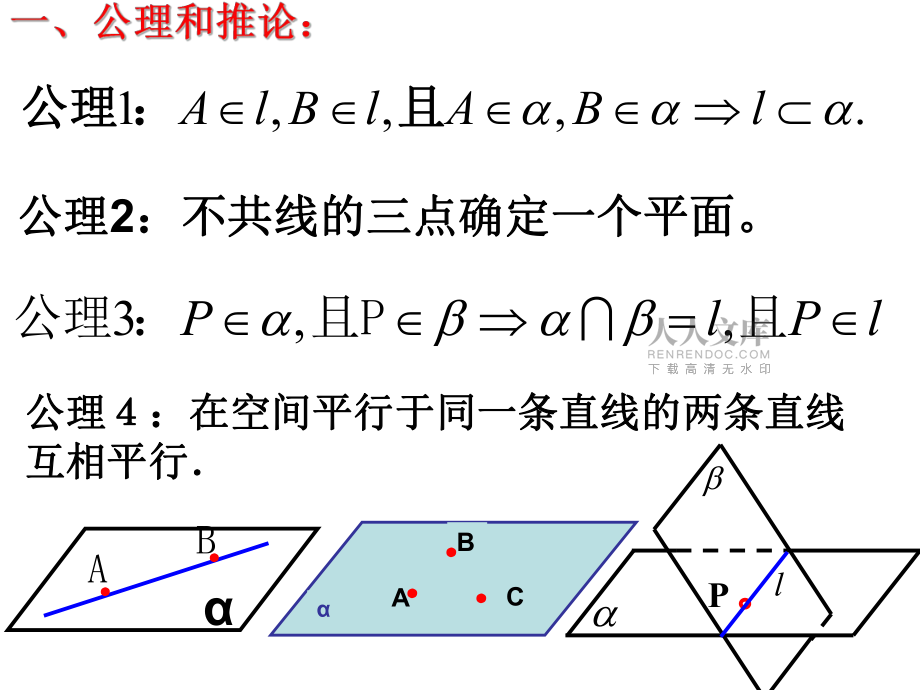
1、AB.,1lBAlBlA且且：公理公理公理公理2：不共线的三点确定一个平面。：不共线的三点确定一个平面。ACB3,PlPl公理 ：且P且Pl公理：在空间平行于同一条直线的两条直线公理：在空间平行于同一条直线的两条直线互相平行互相平行公理公理2：不共线的三点确定一个平面。：不共线的三点确定一个平面。1. 直线直线与与平面平面 平行：平行：（1）定义法：直线与平面无公共点；）定义法：直线与平面无公共点；（2）判定定理：）判定定理： /abaab ab2. 两、面两、面 平行平行:（1）定义法）定义法: 平面与平面无公共点；平面与平面无公共点；/ , / ,/ababPa b 、（2）判定定理：）判

2、定定理：Pba3 3、直线与平面平行的性质定理直线与平面平行的性质定理/aaabba ab b4 4、平面与平面平行的性质定理、平面与平面平行的性质定理面面平行面面平行 线线平行线线平行 ab/aabb5. 直线与平面垂直的判定：直线与平面垂直的判定：（1）定义法：定义法：直线与平面内任意一条直线垂直则线面垂直；直线与平面内任意一条直线垂直则线面垂直；（2）判定定理：判定定理：如果一条直线与一个平面内的两条相交直线都如果一条直线与一个平面内的两条相交直线都,那么该直线与此平面那么该直线与此平面. （线线垂直线线垂直 线面垂直线面垂直）；）； n m llmnBlmn （3）面面垂直的性质：面面

3、垂直的性质：如果两个平面垂直如果两个平面垂直,那么一个平面内垂那么一个平面内垂直于它们交线的直线与另一个平面垂直直于它们交线的直线与另一个平面垂直.lmmll （1）定义法：直线）定义法：直线 l 与平面与平面 内的内的任意一条直线任意一条直线都垂直。都垂直。（2）判定定理：）判定定理：线线垂直线线垂直线面垂直线面垂直al bl abAbalbalA6.判定判定两平面垂直两平面垂直的的方法方法:（1）定义法：定义法：平面与平面相交成直二面角则面面垂直；平面与平面相交成直二面角则面面垂直；（2）判定定理：判定定理：如果一个平面经过另一个平面的垂线，如果一个平面经过另一个平面的垂线，那么这两个平面

4、互相垂直那么这两个平面互相垂直. （线面垂直线面垂直 面面垂直面面垂直）；）；aa 3.线面垂直的性质：线面垂直的性质：垂直于同一个平面的两条直线平垂直于同一个平面的两条直线平行行. / /aabb 4.面面垂直的性质：面面垂直的性质：如果两个平面垂直如果两个平面垂直,那么一个平面那么一个平面内垂直于它们交线的直线与另一个平面垂直内垂直于它们交线的直线与另一个平面垂直./ /aabbab （1）定义法：两个平面相交，如果它们所成的）定义法：两个平面相交，如果它们所成的二面二面角是直二面角角是直二面角。（2）判定定理：）判定定理：线线垂直线线垂直线面垂直线面垂直面面垂直面面垂直aa 面aA8.

5、平面与平面垂直的平面与平面垂直的性质定理：性质定理：laala面面垂直面面垂直线面垂直线面垂直Al1.,/ /aaa例a1.异面直线所成角异面直线所成角：范围：范围求异面直线所成的角的步骤是求异面直线所成的角的步骤是: 一作一作(找找)：作（或找）平行线；作（或找）平行线； 二证：二证：证明所作的角为所求的异面直线所成的角；证明所作的角为所求的异面直线所成的角； 三求：三求：在一恰当的三角形中求出角。在一恰当的三角形中求出角。2. 直线与平面所成角直线与平面所成角：范围：范围 注：已知角，要求角，注：已知角，要求角，关键找射影。关键找射影。3. 二面角二面角：范围：范围OBAAOB即为二面即为

6、二面角角-l-的的平面角。平面角。l l八、补充八、补充：公理：公理： 在空间平行于同一条直线的两条直线互相平行在空间平行于同一条直线的两条直线互相平行空间中，如果两个角的两边分别对应平行，空间中，如果两个角的两边分别对应平行， 那么这两个角相等或互补那么这两个角相等或互补等角定理：等角定理：等角定理等角定理的推论：的推论：如果两条相交直线和另两条相交直线分别平行，如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角（或直角）相等。那么这两组直线所成的锐角（或直角）相等。小结：小结：线线线线平行平行 线面线面 平行平行 面面面面 平行平行线面平行判定线面平行判定线面平行性质线面平

7、行性质面面平行判定面面平行判定面面平行性质面面平行性质空间中的平行关空间中的平行关系的转化系的转化面面平行性质面面平行性质线线线线垂直垂直线面线面垂直垂直面面面面垂直垂直空间中的垂直关系的转化空间中的垂直关系的转化平行和垂直关系的转化平行和垂直关系的转化空间中的平行空间中的平行 空间中的垂直空间中的垂直acb已知已知 , , 如图如图, b, c. aa求证求证:过平面过平面 内一点内一点P作作PA 于于A,作作PB 于于B.cb证明证明:又又aPAaPA同理证明同理证明,PB a.aPB PA=P, PA , PBPBAa(1)求异面直线求异面直线A1B与与B1C所成的角的大小所成的角的大小

8、;(2)求直线求直线A1B与平面与平面BB1D1D所成的角所成的角; (4)求证求证:平面平面A1BD/平面平面CB1D1;(7)求点求点A1到平面到平面CB1D1的距离的距离. 1(5):AC 1 1求求证证 直直线线平平面面A BD;A BD;1(6):ABC 1 1求求证证 平平面面平平面面A BD;A BD;(3)求二面角求二面角ABDA1的正切值的正切值; ABCDA1B1C1D1例如图所示，在长方体中，例如图所示，在长方体中，AB=AD=1，AA1=2，M是棱是棱CC1的中点的中点（）求异面直线）求异面直线A1M和和C1D1所成的角所成的角的正切值；的正切值；（）证明：平面）证明：平面ABM平面平面A1B1M1例如图，例如图， 在矩形在矩形 中，点中，点 分别在线段分别在线段 上，上， .沿直线沿直线 将将 翻折翻折成成 ，使平面，使平面 . （）求二面角）求二面角 的余弦值；的余弦值；（）点）点 分别在线段分