自动控制理论 根轨迹法课件

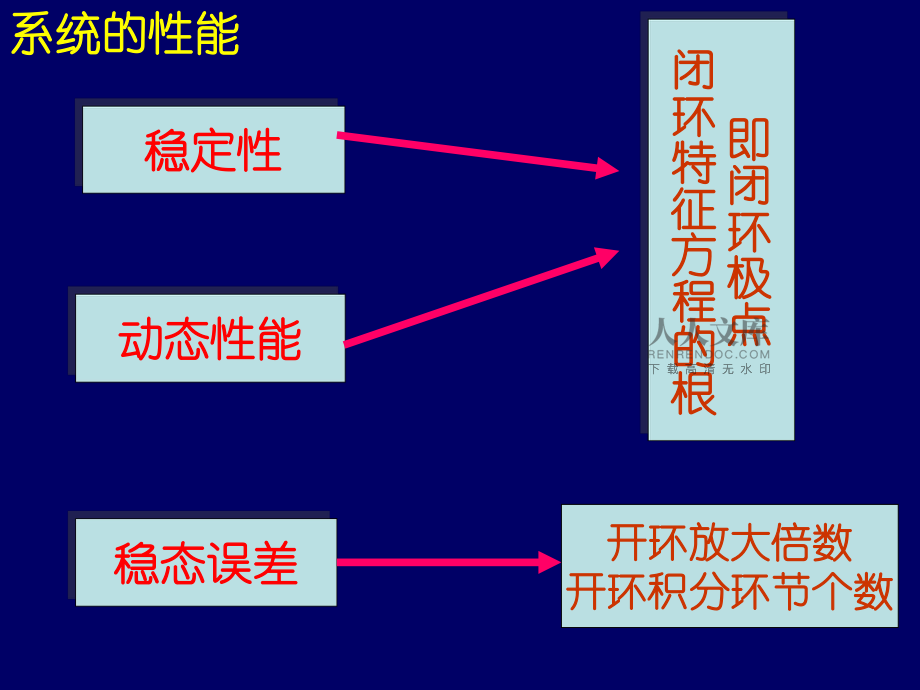
1、第四章第四章 根轨迹法根轨迹法目的目的 掌握绘制系统根轨迹的方法掌握绘制系统根轨迹的方法掌握利用根轨迹分析系统的方法掌握利用根轨迹分析系统的方法内容内容根轨迹方程根轨迹方程绘制根轨迹的基本法则绘制根轨迹的基本法则利用根轨迹进行系统分析利用根轨迹进行系统分析稳定性稳定性即闭环极点即闭环极点闭环特征方程的根闭环特征方程的根动态性能动态性能稳态误差稳态误差系统的性能系统的性能开环放大倍数开环放大倍数开环积分环节个数开环积分环节个数困困 难难! !困难困难1 1：系统闭环特征方程的根如何求取！：系统闭环特征方程的根如何求取！困难困难2 2：讨论或预测当系统中的某一参数发生：讨论或预测当系统中的某一参数

2、发生 变化时系统闭环特征方程的根如何变变化时系统闭环特征方程的根如何变 化化! ! 参数改变，系统性能如何改变！参数改变，系统性能如何改变！ 伊万思伊万思第一节第一节 根轨迹法的基本概念根轨迹法的基本概念 R(s)C(s) 1( ssKg+-) 1()(ssKsGgoggcKssKsG2)(1.1.引例引例讨论讨论Kg变化时闭环极点的变化。变化时闭环极点的变化。02gKssgKs4121212, 1开环传递函数开环传递函数闭环传递函数闭环传递函数闭环极点闭环极点特征方程特征方程 s 平面 j 0 -1 -0.5 kg=0.5 kg=0.25 kg=0 kg=0 kg=0.5 闭环极点在闭环极点

3、在S S平平面上的变化面上的变化 系统的开环传递函数中某一参数变化时，系统闭系统的开环传递函数中某一参数变化时，系统闭环特征方程的根在环特征方程的根在S S平面上的变化轨迹即为平面上的变化轨迹即为根轨迹根轨迹gKs4121212, 1 问题：问题：绘制根轨迹是用描点法吗？绘制根轨迹是用描点法吗？高阶系统闭环特征方程的根的表达高阶系统闭环特征方程的根的表达 式如何求式如何求?思路：思路：利用利用开环传函开环传函绘制闭环特征绘制闭环特征方程的根的变化。方程的根的变化。2.2.根轨迹的幅值条件和相角条件根轨迹的幅值条件和相角条件 R(s) C(s) + - G(s) H(s) )(1)()()(1)

4、()()()(sGsGsHsGsGsRsCsGoc0)(1sGo闭环特征方程闭环特征方程1)(sGo1)(gosssG) 12(180)(argksssGgo)()()(11inijmjgopszsKsG1)()(11ginijmjgsspszsK) 12(180)()(arg11ksspszsKginijmjg若开环传递函数若开环传递函数则根轨迹的条件方程为则根轨迹的条件方程为幅值条件幅值条件相（幅）相（幅）角条件角条件根轨迹增益根轨迹增益开环零点开环零点-zj-pi开环极点开环极点11mjjogniizKKp开环增益开环增益注注: (1)不计原点处的零值极点；不计原点处的零值极点； （2）

5、m=0时时根轨迹增益根轨迹增益11mjjz第二节第二节 绘制根轨迹的基本法则绘制根轨迹的基本法则 1. 1. 根轨迹的连续性根轨迹的连续性 根轨迹是连续变化的曲线根轨迹是连续变化的曲线2. 2. 根轨迹的对称性根轨迹的对称性 根轨迹对称于实轴根轨迹对称于实轴3. 3. 根轨迹的分支数根轨迹的分支数 n 阶系统，阶系统，n 条根轨迹。条根轨迹。4. 4. 根轨迹的起点和终点根轨迹的起点和终点Kg=0 时的闭环极点为根轨迹的起点时的闭环极点为根轨迹的起点Kg 时的闭环极点为根轨迹的终点时的闭环极点为根轨迹的终点 n 条根轨迹起始于系统的条根轨迹起始于系统的n 个开环极点个开环极点 n 条根轨迹终止

6、于系统的条根轨迹终止于系统的n个开环零点个开环零点 m1212，根，根轨迹中有两条分支进入轨迹中有两条分支进入s s的右半平面，这表明的右半平面，这表明附加零点对系统根轨迹的影响甚小，即系统的附加零点对系统根轨迹的影响甚小，即系统的动态性能不会因此而有明显的改善，其原因是动态性能不会因此而有明显的改善，其原因是该零点距离虚轴较远。该零点距离虚轴较远。（2 2）假设零点）假设零点- -b位于位于 间的实轴段上，间的实轴段上，若令若令b b =1.2=1.2，即，即13(1.2)( )( )(1)(3)K sG s H ss ss (4-53)据此作出系统的根轨迹如图据此作出系统的根轨迹如图4-3

7、14-31所示。所示。图4-31 根轨迹图由图可见，当由图可见，当K K在在 范围内变化时，该系统范围内变化时，该系统总是稳定的。总是稳定的。0 （3 3）假设零点）假设零点- -b 位于位于 间的实轴段上，若间的实轴段上，若令令b=0.4=0.4，即，即01 (0.4)( )( )(1)(3)K sG s H ss ss (4-54)图4-32 根轨迹图据此，作出系统的根轨迹图如图据此，作出系统的根轨迹图如图4-324-32所示。所示。由图可知：由图可知：1 1）当）当K 由由 变化时，系统的根轨迹都位于变化时，系统的根轨迹都位于s s平面的左方，因而该系统总是稳定的。平面的左方，因而该系统

8、总是稳定的。 0 2 2）当）当 kk1，3个闭环极点中同样有一对共轭复数个闭环极点中同样有一对共轭复数极点极点s1、s2和一个实数极点和一个实数极点s3，但由于极点，但由于极点s3距距虚轴很近，因而相应的瞬态分量衰减得很缓慢，虚轴很近，因而相应的瞬态分量衰减得很缓慢，从而导致系统的输出响应有较长的过渡过程时间，从而导致系统的输出响应有较长的过渡过程时间，这是一般的控制系统所不希望的。这是一般的控制系统所不希望的。 由上述分析可知，增加的开环零点于由上述分析可知，增加的开环零点于s s平面实轴上的不同位置，它对系统根轨迹平面实轴上的不同位置，它对系统根轨迹所产生的影响是不同的。所产生的影响是不

9、同的。 对于某一具体的开环传递函数，只有选对于某一具体的开环传递函数，只有选择合适的附加零点，才有可能使控制系统择合适的附加零点，才有可能使控制系统的稳定性及动态性能得到显著地改善。的稳定性及动态性能得到显著地改善。 122okGss 例：-20j系统不稳定系统不稳定-20j-41 1）增加零点）增加零点4 z系统仍不稳定系统仍不稳定0j0j2z 系统为临界稳定系统为临界稳定 1z 系统稳定系统稳定2 2）增加零点）增加零点3 3）增加零点）增加零点增加增加合适的合适的开环零点将使根轨迹开环零点将使根轨迹向左向左弯曲或移动弯曲或移动，可以，可以改善系统的稳定性改善系统的稳定性和快速性和快速性，

10、而且增加的开环零点越靠，而且增加的开环零点越靠近原点对系统改善性能越好。近原点对系统改善性能越好。结结 论论2. 2. 增加开环极点增加开环极点 若在开环传递函数中增加一个开环极点，若在开环传递函数中增加一个开环极点，-p (p0)，则在根轨迹的相角方程中，则在根轨迹的相角方程中增加了一个负角增加了一个负角-arg(s+p)，从而导致系统，从而导致系统的根轨迹作向右倾斜变化，这显然不利于的根轨迹作向右倾斜变化，这显然不利于系统的稳定性及动态性能的改善。系统的稳定性及动态性能的改善。0例如：设一单位反馈系统的开环传递函例如：设一单位反馈系统的开环传递函数为数为( )(1)KG ss s 由图可知

11、，当参变量由图可知，当参变量K 由由 变化时，变化时，该系统总是稳定的。该系统总是稳定的。系统的根轨迹如下图所示系统的根轨迹如下图所示0 如增加一个开环极点如增加一个开环极点-2-2，则开环传递函数，则开环传递函数变为变为( )( )(1)(2)KG s H ss ss 对应的根轨迹如下图所示。对应的根轨迹如下图所示。当当K 66时，系统就变时，系统就变为不稳定了。为不稳定了。 2oKGs s 例：K 取何值也稳定（如图所示）。取何值也稳定（如图所示）。 -20j-1-20j-4ds2222当当0K6时系统稳定时系统稳定314p ）增加：-2jds-220322p ）增加：当当0K4时系统稳定

12、时系统稳定-2j0330p ）增加：，K取何值都不稳定。取何值都不稳定。 p3在在-，0之间之间 为条件稳定，为条件稳定，p3越越 靠近原点靠近原点, 使系统使系统 稳定的稳定的K取值范围越取值范围越小。当小。当p3 在原点时，在原点时，K取何值系统都不稳取何值系统都不稳定。定。 增加开环极点将使根轨迹增加开环极点将使根轨迹向右弯曲或向右弯曲或右移右移，从而使系统的稳定性和快速性，从而使系统的稳定性和快速性变差；而且所增加极点的模值越小，变差；而且所增加极点的模值越小，这种影响越明显。这种影响越明显。结结 论论第六节第六节 用根轨迹法分析控制系统用根轨迹法分析控制系统利用绘制的根轨迹进行系统分

13、析利用绘制的根轨迹进行系统分析C 稳定性稳定性C 动态性能动态性能C 稳态误差稳态误差利用绘制的根轨迹进行系统设计利用绘制的根轨迹进行系统设计C根据性能指标要求确定系统参数根据性能指标要求确定系统参数1. 1. 用根轨迹法确定系统中的有关参数用根轨迹法确定系统中的有关参数图图4-35 4-35 控制系统控制系统 试用选择参数试用选择参数K K1 1和和K K2 2以使系统满足下列性以使系统满足下列性能指标能指标 sss r tt;e0.351 2 t3s 121210.35ssvK KeKK 解解 系统的开环传递函数系统的开环传递函数 112Gs2oKs sK K 系统的静态速度误差系数系统的

14、静态速度误差系数 1122vKKK K 若要满足系统误差的要求，若要满足系统误差的要求，K K1 1必须取值必须取值较大，较大，K K2 2必须取值较小。必须取值较小。由题意得由题意得 为了同时满足为了同时满足 的要求，闭环极点必的要求，闭环极点必须位于图须位于图4-364-36所示的所示的阴影区域内。阴影区域内。在在S左半平面上左半平面上,过坐标原点作一与负实轴过坐标原点作一与负实轴成成45角的射线角的射线,如图如图4-36所示所示图4-36 在S平面上希望极点的区域s44 t34 3ns 因即st 和设设 ，则式（，则式（4-574-57）变为）变为令令 ，则图，则图4-35所示系统所示系

15、统的闭环特征方程为的闭环特征方程为作出以 为参变量的根轨迹如图4-37所示。 2 s2s0 10 4-58s s2 或（）121KK K ， 2120 4-57G ssss 0 为了满足静态性能的要求，试取为了满足静态性能的要求，试取则式（则式（4-57）可写为）可写为1=20K 2s10 4-59 s2s20 图4-37 式（4-58）的根轨迹式中开环传递函数的极式中开环传递函数的极点为点为-3.15-3.15j3.17j3.17。以以为参变量的根轨迹如图为参变量的根轨迹如图4-384-38所示所示, ,该图该图与由过坐标原点作一与负实轴成与由过坐标原点作一与负实轴成4545角的角的直线；并

16、与根轨迹相交于直线；并与根轨迹相交于-3.15-3.15j3.17j3.17。由根轨迹幅值条件求得由根轨迹幅值条件求得=4.3=20K=4.3=20K2 2 ；即；即 K K2 2=0.215=0.215因为所求闭环极点实部因为所求闭环极点实部=3.15;=3.15;因而因而121441.2733.152220 0.2150.3150.3520ssstssK KeK 图4-38 式（4-59）的根轨迹2. 2. 确定指定确定指定K0 0时的闭环传递函数时的闭环传递函数 控制系统的闭环零点由开环传递函数控制系统的闭环零点由开环传递函数中中G(sG(s) )的零点和的零点和H(sH(s) )的极点

17、组成，它们的极点组成，它们一般均为已知。系统的闭环极点与根轨一般均为已知。系统的闭环极点与根轨迹的增益迹的增益Ko有关。如果有关。如果Ko已知，就可以已知，就可以沿着特定的根轨迹分支，根据根轨迹的沿着特定的根轨迹分支，根据根轨迹的幅值条件，用试探法求得响应的闭环极幅值条件，用试探法求得响应的闭环极点。点。求K0=0.5时的闭环传递函数。解 在分离点S=-0.423处，由幅值条件求得K0=0.385由此可知，K0=0.5时，系统有一对共轭复根和一个实根，经试样法确定，当s3=-2.192时，K00.5 012KG s H ss ss 例例 已知图4-39 根轨迹图 220.52.1920.404

18、0.256C sR sss 一对共轭极点的对应的多项式为一对共轭极点的对应的多项式为 322120.5320.52.1922.192 0.8080.229s sssssssss 22,3 0.8080.22900.4040.256sssj 令得系统的传递函数为系统的传递函数为 根据指定的阻尼比 值，由根轨迹图的坐标原点作一与负实轴夹角为 的射线。该射线与根轨迹的交点就是所求的一对闭环主导极点，由幅值条件确定这对极点对应的Ko值，并据此确定闭环的其他极点。3. 3. 确定具有指定阻尼比确定具有指定阻尼比 的闭环极点的闭环极点和单位阶跃响应和单位阶跃响应=arccos 1）闭环极点和相应的增益2）

19、单位阶跃信号作用下的输出响应 1,21233302222arccos0.5600.330.580.330.580.330.583s2.34 1.051.051 ; 2.340330.581.052.340330.58010.1 0.92.34sjsssjjsKC sR ssR sssC ss sssss 令 222.340.33330.580330.5810.10.9cos0.58sin0.58ttsC teett 仍以图4-8所示系统为例，令 ，试求=0.5 4. 4. 稳定性分析稳定性分析思路：关键点，根轨迹与虚轴的思路：关键点，根轨迹与虚轴的交点交点。)22)(3()2()(2sssss

20、KsGgo例：例： 利用根轨迹分析系统稳定时根轨迹增益的取值范利用根轨迹分析系统稳定时根轨迹增益的取值范围。围。系统开环传函为系统开环传函为 参数在一定范围内取值才能稳定的系统称为条件参数在一定范围内取值才能稳定的系统称为条件稳定系统。条件稳定系统可利用根轨迹分析系统稳定系统。条件稳定系统可利用根轨迹分析系统稳定时参数（根轨迹增益）的取值范围。稳定时参数（根轨迹增益）的取值范围。 0 j s 平面 1.6j (Kg=7.0) 1.6j 解解: :绘制根轨迹如图绘制根轨迹如图0 kg 7 系统稳定时根轨迹增益的取值范围为系统稳定时根轨迹增益的取值范围为22(24)( )(4)(6)(1.41)oK ssG ss ssss例：例：系统开环传函为系统开环传函为试作稳定性分析。试作稳定性分析。解解: :画出以下根轨迹：画出以下根轨迹：由图可见，由图可见，当当0K14及及64K195时，时，闭环系统稳定。闭环系统稳定。当当14K195时，时，系统不稳定。系统不稳定。5. 5. 暂态性能分析暂态性能分析 利用