应力状态分析与强度理论PPT学习教案

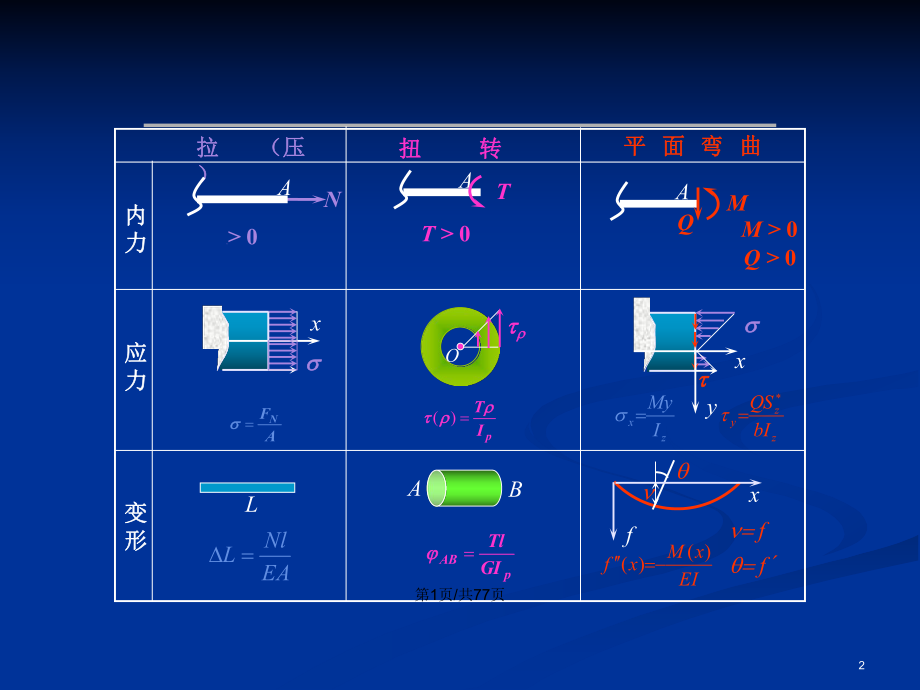
1、会计学1应力状态分析与强度理论应力状态分析与强度理论2拉拉 （压（压）扭扭 转转平 面 弯 曲平 面 弯 曲内内力力应应力力变变形形NN 0AT 0ATAMQM 0Q 0 xs sAFNs sLEANlL Ot tr rpITr rr rt t)(zxIMyss st txyzzybIQStABpABGITl qnfxq fn fEIxMxf)()( 第1页/共77页3拉拉 （压（压）扭扭 转转平 面 弯 曲平 面 弯 曲强强度度条条件件刚刚度度条条件件maxssmaxminsNAmaxsANmaxtt|maxtTWn|maxtnWTmaxssmaxttmaxsMWzmaxszWMmaxqqm

2、axqqLyLy|max第2页/共77页481 应力状态的概念应力状态的概念第3页/共77页5QMzN第4页/共77页6低碳钢低碳钢 塑性材料拉伸时为什么会出现滑移线？塑性材料拉伸时为什么会出现滑移线？铸铸 铁铁第5页/共77页7脆性材料扭转时为什么沿脆性材料扭转时为什么沿4545螺旋面断开？螺旋面断开？低碳钢低碳钢铸铸 铁铁第6页/共77页8 不仅横截面上存在应力，斜截面上也存在不仅横截面上存在应力，斜截面上也存在应力；不仅要研究横截面上的应力，而且应力；不仅要研究横截面上的应力，而且也要研究斜截面上的应力。也要研究斜截面上的应力。第7页/共77页9tsytxtys ts第8页/共77页10

3、哪一个面上哪一个面上哪一点哪一点？ 哪一点哪一点哪个方向面？哪个方向面？第9页/共77页11第10页/共77页12dzdydx0dzdydx第11页/共77页13第12页/共77页141s2s3syxzs sxs sys szt txyt tyxt tyzt tzyt tzxt txz 单元体上没有切应力的面称为单元体上没有切应力的面称为主平面主平面；主平面上的正应力；主平面上的正应力称为称为主应力，主应力，分别用分别用 表示，并且表示，并且该单元体称为该单元体称为主应力单元。主应力单元。321,sss321s ss ss s 8-1 应力状态的概念应力状态的概念第13页/共77页151s2s

4、3s空间（三向）应力状态：三个主应力均不为零空间（三向）应力状态：三个主应力均不为零平面（二向）应力状态：一个主应力为零平面（二向）应力状态：一个主应力为零单向应力状态：两个主应力为零单向应力状态：两个主应力为零第14页/共77页16x xy ysxs syt tyxt txy 0 nF 0 tF1.1.斜截面上的应力斜截面上的应力s sy as att txyd dA Axsyxt 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第15页/共77页17 由由x x正向逆时针转到正向逆时针转到n n正正向者为正；反之为负。向者为正；反之为负。ntx正正 应应 力力yssx拉应力为正

5、拉应力为正sx压应力为负压应力为负切 应 力 tytxt 使单元体或其局部顺使单元体或其局部顺时针方向转动为正；反之时针方向转动为正；反之为负。为负。第16页/共77页18 0 nF0sin)sin(cos)sin(cos)cos(sin)cos(ststsdAdAdAdAdAyyxxxy 0 tF0cos)sin(sin)sin(sin)cos(cos)cos(ststtdAdAdAdAdAyyxxxys sy as att txyd dA Axsyxt 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第17页/共77页19利用三角函数公式利用三角函数公式)2cos1(21cos

6、2 )2cos1(21sin2 2sincossin2 并注意到并注意到 化简得化简得xyyxt tt t tsssss2sin2cos)(21)(21xyyxyxtsst2cos2sin)(21xyyx 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第18页/共77页20tsssss2sin2cos)(21)(21xyyxyx确定正应力极值确定正应力极值tsss2cos22sin)(xyyxdd设设0 0 时，上式值为零，即时，上式值为零，即02cos22sin)(00tssxyyx3. 正正应力极值和方向应力极值和方向0 022cos2cos2sin2sin22 2) )(2

7、 20 00 0 xyxy0 0y yx x即即0 0 时，切应力为零时，切应力为零 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第19页/共77页21yxxys ss st t 22tan0 由上式可以确定出两个相互垂直的平面，分别由上式可以确定出两个相互垂直的平面，分别为最大正应力和最小正应力所在平面。为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为：所以，最大和最小正应力分别为： 22max4212xyyxyxt ts ss ss ss ss s 22min4212xyyxyxt ts ss ss ss ss s 主应力按代数值排序：主应力按代数值排序：1

8、 1 2 2 3 3 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第20页/共77页22确定切应力极值确定切应力极值02sin22cos)( t t s ss s t t xyyxdd4. 切切应力极值和方向应力极值和方向x xy yy yx x2 2) )( (t t t t2tan 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态tsst2cos2sin)(21xyyx2 22 22 21 1xyxyxyxyy yx xminminmax,max,22)(t tt tt t第21页/共77页23试求试求（1 1） 斜面上的应力；斜面上的应力； （2 2）主应力、

9、主平面；）主应力、主平面； （3 3）绘出主应力单元体。）绘出主应力单元体。例题例题1 1：一点处的平面应力状态如图所示。一点处的平面应力状态如图所示。 ys s xs sxyt t。30MPa，60 xsMPa,30 xyt,MPa40ys已知已知 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第22页/共77页24解：解： （1 1） 斜面上的应力斜面上的应力tsssss2sin2cos22xyyxyx)60sin(30)60cos(2406024060MPa02. 9tsst2cos2sin2xyyx)60cos(30)60sin(24060MPa3 .58ys s xs

10、sxyt t 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第23页/共77页25（2 2）主应力、主平面）主应力、主平面2yxssxyyx22)2(tssmaxsMPa3 .682yxssxyyx22)2(tssminsMPa3 .48MPa3 .48, 0MPa,3 .68321sssys s xs sxyt t 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第24页/共77页26主平面的方位：主平面的方位：yxxytgsst2206 . 0406060,5 .1505 .105905 .150ys s xs sxyt t代入代入 表达式可知表达式可知 s s主

11、应力主应力 方向：方向：1s5 .150主应力主应力 方向：方向：3s s5 .1050 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第25页/共77页27（3 3）主应力单元体：）主应力单元体：ys s xs sxyt t5 .151s3s 8-2 8-2 解析法分析二向应力状态解析法分析二向应力状态第26页/共77页28tsssss2sin2cos)(21)(21xyyxyxtsst2cos2sin)(21xyyxxyyxyx2222)2()2(t ts ss st ts ss ss s 这个方程恰好表示一个圆，这个圆称为应力圆这个方程恰好表示一个圆，这个圆称为应力圆 8-

12、3 8-3 图解法分析二向应力状态图解法分析二向应力状态第27页/共77页29xyyxyx2222)2()2(tsstsssstRCxyyxR22)2(t ts ss s 2yxss1. 1. 应力圆：应力圆： 8-3 8-3 图解法分析二向应力状态图解法分析二向应力状态第28页/共77页302.2.应力圆的画法应力圆的画法stD(s sx ,t txy)D/(s sy ,t tyx)cs ss sxy 2RxyyxR22)2(t ts ss s ys st tyxt txyADxs 8-3 8-3 图解法分析二向应力状态图解法分析二向应力状态第29页/共77页31点面对应点面对应应力圆上某一

13、点的坐标值对应着应力圆上某一点的坐标值对应着微元某一截面上的正应力和切应力微元某一截面上的正应力和切应力3 3、几种对应关系、几种对应关系stD(s sx ,t txy)D/(s sy ,t tyx)cs ss sxy 2s syt tyxt txysxH ),(aatsH 2 8-3 8-3 图解法分析二向应力状态图解法分析二向应力状态第30页/共77页32二倍角对应二倍角对应半径转过的角度是斜截面旋转角度的两半径转过的角度是斜截面旋转角度的两倍。倍。第31页/共77页33试用应力圆法计算图示单元体试用应力圆法计算图示单元体e-fe-f截面上的应力截面上的应力。图中应力的单位为。图中应力的单

14、位为MPaMPa。4 . 42 . 2n030ef stoadcMPa2 . 5030ssMPa8 . 0030tt060第32页/共77页34第33页/共77页35切应力等于零的截面为主平面主平面上的正应力称为主应力a(s sx ,t tx)d(s sy ,t ty)cs ss sxy 2 sto222222xyxyxtsstsss22122xyxyxt ts ss ss ss ss s1s2s02yxxtgsst2200002)90(2tgtg22222xyxyxtsssssmaxt tmint t第34页/共77页36222122maxs ss st ts ss st txyx22212

15、2mins ss st ts ss st txyx第35页/共77页37分析圆轴扭转时最大切应力的作用面，说明铸铁分析圆轴扭转时最大切应力的作用面，说明铸铁圆试样扭转破坏的主要原因。圆试样扭转破坏的主要原因。t ss ss sxy 2ss2cos2yxt2sinxts2sin tss2sin2yxt2cosxtt2cos045tssmax450tssmax4500045tminsmaxs 铸铁圆试样扭转试验时，正是沿着最大拉应力作用面（即450螺旋面）断开的。因此，可以认为这种脆性破坏是由最大拉应力引起的。第36页/共77页38分析轴向拉伸杆件的最大切应力的作用面，说明分析轴向拉伸杆件的最大切

16、应力的作用面，说明低碳钢拉伸时发生屈服的主要原因。低碳钢拉伸时发生屈服的主要原因。低碳钢拉伸时，其上任意一点都是单向应力状态。xs ss ss sxy 2ss2cos2yxt2sinx s ss ss s 2cos22xx tss2sin2yxt2cosxst2sin2x0452045xss2045xstmaxt 低碳钢试样拉伸至屈服时表面沿450出现滑移线，是由最大切应力引起的。第37页/共77页39轴向拉伸压缩st2sin2 x)2cos1 (2 ssxxss 10 32ss2minmaxxst ss ss sxy 2ss2cos2yxt2sinx tss2sin2yxt2cosx第38页

17、/共77页40扭 转tt2cos x t ts s 2sin xxts 1x3- tsxttminmax ss ss sxy 2ss2cos2yxt2sinx tss2sin2yxt2cosx0 2s s第39页/共77页41弯 曲平面应力状态的几种特殊情况22minmax)2(xxtst tss2sin2yxt2cosx ss ss sxy 2ss2cos2yxt2sinx221322xxxtssstsss2sin2cos22xxxtst2cos2sin2xx22 1322xyxyxt ts ss ss ss ss s第40页/共77页42xmqm43215x第41页/共77页43mm432

18、15x3s3s3s3s1s1s1s1s3s3sxxxx1s3s1s3s1s1ssssssttttt第42页/共77页44在梁的xy平面内可以绘制两组正交的曲线，在一组曲线上每一点处切线的方向是该点处主应力 （拉应力）的方向，而在另一组曲线上每一点处切线的方向则为主应力 (压应力)的方向。这样的曲线就称为梁的主应力迹线。1s3s梁的主应力迹线第43页/共77页451.1.定义定义2s3s1s三个主应力都不为零的应力状态三个主应力都不为零的应力状态 8-5 8-5 三向应力状态三向应力状态第44页/共77页46由三向应力圆可以看出：由三向应力圆可以看出：231maxs ss st t 结论：结论：

19、代表单元体任意斜代表单元体任意斜截面上应力的点，截面上应力的点，必定在三个应力圆必定在三个应力圆圆周上或圆内。圆周上或圆内。213s s32s s1s st ts s 8-5 8-5 三向应力状态三向应力状态第45页/共77页471. 1. 基本变形时的胡克定律基本变形时的胡克定律xxE s s Exxys s xsyx1 1）轴向拉压胡克定律）轴向拉压胡克定律横向变形横向变形2 2）纯剪切胡克定律）纯剪切胡克定律 t tG t 8-6 8-6 广义胡克定律广义胡克定律第46页/共77页48xsEsnn-泊松比泊松比Esn2s1s3s=1s1s1+1 2s2s+3s3s1 E11sE21sn

20、E31sn 1+ 32111s ss sn ns s E第47页/共77页492s3s1s32111sssE13221sssE21331sssE第48页/共77页502s3s1s 32111s ss sn ns s E 13221s ss sn ns s E 21331s ss sn ns s EzyxxEssns1xzyyEssns1yxzzEssns1主应变与主应力方向重合主应变与主应力方向重合第49页/共77页51)(1zyxxEs ss s s s Gxyxyt t 3 3、广义胡克定律的一般形式、广义胡克定律的一般形式)(1xzyyEs ss s s s )(1yxzzEs ss s

21、 s s Gyzyzt t Gzxzxt t s sxs sys szt txyt tyxt tyzt tzyt tzxt txz 8-6 8-6 广义胡克定律广义胡克定律第50页/共77页52 某点的应力状态如图所示,当x,y,z不变,x增大时,关于x值的说法正确的是_.A. 不变B. 增大C. 减小D. 无法判定ys sxs szs sx仅与正应力有关，而与切应力无关。所以当切应力增大时，线应变不变。AzyxxEssns1第51页/共77页53 一受扭圆轴,直径d=20mm,圆轴的材料为 钢,E=200GPa,=0.3.现测得圆轴表面上与轴线成450方向的应变为=5.210-4,试求圆轴所

22、承受的扭矩.T045pWTt1s3sts102sts332111ssnsEnttE11tnE1n1163dET3 . 0116210200102 . 5334Nm7 .125第52页/共77页54qs s1s s2s s31a2a3a111aa 222aa 333aa 332211111aaaVVVV q 321321332211111aaaaaaaaa3213213213211aaaaaaaaa321q32121sssnqE31ss02s0qs sxs sys szzyxEsssnq21KEms ss ss ss sn nq q3)21 ( 3321第53页/共77页55l1lFllFFOl

23、LNLFW2121NV21 EANLLLEALN22应变能密度应变能密度: : 单位体积内的应变能VVv ALLF21ss21第54页/共77页568.9 空间应力状态下的应变能密度Ev2212ss1s12s1s22nE11sEW2211sEW2222sE22sE21ssn1s2s3s3s3nE33s3nEW2233sE31ssnE32ssnW321WWWE221sE222sE21ssnE223sE31ssnE32ssn133221232221221ssssssnsssE21331322321121ssnssssnssssnssE1E2E3E33221121sssv第55页/共77页57s s

24、1s s2s s3s ss ss s222222221sssnsssEvv3321ssss232221621sssnEvvdvvvvvdvvv 21232322222161ssssssnEvd133221232221221ssssssnsssE第56页/共77页58max,maxssAFN（拉压）（拉压）maxmaxs ss s WM（弯曲）（弯曲）（正应力强度条件）（正应力强度条件）*maxttzzsbISF（弯曲）（弯曲）（扭转）（扭转）maxttpWT（切应力强度条件）（切应力强度条件）maxs ss s maxt tt t 1. 1. 杆件基本变形下的强度条件杆件基本变形下的强度条件8

25、-10 8-10 强度理论概述强度理论概述第57页/共77页59maxs smaxt t满足满足maxs ss s maxt tt t 是否强度就没有问题了？是否强度就没有问题了？第58页/共77页60强度理论：强度理论：人们根据大量的破坏现象，通过判断推人们根据大量的破坏现象，通过判断推理、概括，提出了种种关于破坏原因的假说，找出理、概括，提出了种种关于破坏原因的假说，找出引起破坏的主要因素，经过实践检验，不断完善，引起破坏的主要因素，经过实践检验，不断完善，在一定范围与实际相符合，上升为理论。在一定范围与实际相符合，上升为理论。 为了建立复杂应力状态下的强度条件，而提出为了建立复杂应力状态

26、下的强度条件，而提出的关于材料破坏原因的假设及计算方法。的关于材料破坏原因的假设及计算方法。第59页/共77页61构件由于强度不足将引发两种失效形式构件由于强度不足将引发两种失效形式 (1) (1) 脆性断裂：材料无明显的塑性变形即发生断裂，脆性断裂：材料无明显的塑性变形即发生断裂，断面较粗糙，且多发生在垂直于最大正应力的截面上，断面较粗糙，且多发生在垂直于最大正应力的截面上，如铸铁受拉、扭，低温脆断等。如铸铁受拉、扭，低温脆断等。关于关于屈服的强度理论：屈服的强度理论：最大切应力理论和畸变能密度理论最大切应力理论和畸变能密度理论 (2) (2) 塑性屈服（流动）：材料破坏前发生显著的塑性塑性

27、屈服（流动）：材料破坏前发生显著的塑性变形，破坏断面粒子较光滑，且多发生在最大剪应力面变形，破坏断面粒子较光滑，且多发生在最大剪应力面上，例如低碳钢拉、扭，铸铁压。上，例如低碳钢拉、扭，铸铁压。关于关于断裂的强度理论：断裂的强度理论：最大拉应力理论和最大伸长线应变理论最大拉应力理论和最大伸长线应变理论第60页/共77页621. 1. 最大拉应力理论最大拉应力理论（第一强度理论）（第一强度理论） 材料发生断裂的主要因素是最大拉应力达到极限值材料发生断裂的主要因素是最大拉应力达到极限值01s ss s 构件危险点的最大拉应力构件危险点的最大拉应力1s s 极限拉应力，由单拉实验测得极限拉应力，由单

28、拉实验测得bs ss s 00s s第61页/共77页63b1s ss s 断裂条件断裂条件 s ss ss s nb1强度条件强度条件1. 1. 最大拉应力理论（第一强度理论）最大拉应力理论（第一强度理论）铸铁拉伸铸铁拉伸铸铁扭转铸铁扭转第62页/共77页642. 2. 最大伸长拉应变理论最大伸长拉应变理论（第二强度理论）（第二强度理论） 无论材料处于什么应力状态无论材料处于什么应力状态, ,只要发生脆性断裂只要发生脆性断裂, ,都是由于微元内的最大拉应变（线变形）达到简单都是由于微元内的最大拉应变（线变形）达到简单拉伸时的破坏伸长应变数值。拉伸时的破坏伸长应变数值。 01 构件危险点的最大

29、伸长线应变构件危险点的最大伸长线应变1 极限伸长线应变，由单向拉伸实验测得极限伸长线应变，由单向拉伸实验测得0 E/)(3211s ss s s s Eb/0s s 第63页/共77页65实验表明：实验表明：此理论对于一拉一压的二向应力状态的脆此理论对于一拉一压的二向应力状态的脆性材料的断裂较符合，如铸铁受拉压比第一强度理论性材料的断裂较符合，如铸铁受拉压比第一强度理论更接近实际情况。更接近实际情况。强度条件强度条件)(321sssssnb2. 2. 最大伸长拉应变理论最大伸长拉应变理论（第二强度理论）（第二强度理论）断裂条件断裂条件EEbssss)(1321bssss)(321即即第64页/

30、共77页66 无论材料处于什么应力状态无论材料处于什么应力状态, ,只要发生屈服只要发生屈服, ,都都是由于微元内的最大切应力达到了某一极限值。是由于微元内的最大切应力达到了某一极限值。0maxt tt t 3. 3. 最大切应力理论最大切应力理论（第三强度理论）（第三强度理论） 构件危险点的最大切应力构件危险点的最大切应力maxt t 极限切应力，由单向拉伸实验测得极限切应力，由单向拉伸实验测得0t t2/0ss st t 2/ )(31maxsst第65页/共77页67s31s ss ss s 屈服条件屈服条件 s ss ss ss s ss31n强度条强度条件件3. 3. 最大切应力理论

31、最大切应力理论（第三强度理论）（第三强度理论）低碳钢拉伸低碳钢拉伸低碳钢扭转低碳钢扭转第66页/共77页68实验表明：实验表明：此理论对于塑性材料的屈服破坏能够得到此理论对于塑性材料的屈服破坏能够得到较为满意的解释。并能解释材料在三向均压下不发生较为满意的解释。并能解释材料在三向均压下不发生塑性变形或断裂的事实。塑性变形或断裂的事实。)0(maxt局限性：局限性： 2 2、不能解释三向均拉下可能发生断裂的现象，、不能解释三向均拉下可能发生断裂的现象，1 1、未考虑、未考虑 的影响，试验证实最大影响达的影响，试验证实最大影响达15%15%。2s3. 3. 最大切应力理论最大切应力理论（第三强度理

32、论）（第三强度理论）第67页/共77页69 无论材料处于什么应力状态无论材料处于什么应力状态, ,只要发生屈服只要发生屈服, ,都是都是由于微元的最大畸变能密度达到一个极限值。由于微元的最大畸变能密度达到一个极限值。0sfsfvv 4. 4. 畸变畸变能密度理论能密度理论（第四强度理论）（第四强度理论） 213232221sf)()()(61s ss ss ss ss ss sn n Ev 构件危险点的畸变能密度构件危险点的畸变能密度sfn n20f261ssEvsn 形状改变比能的极限值，由单拉实验测得形状改变比能的极限值，由单拉实验测得0f sn n第68页/共77页70屈服条件屈服条件22132322212)()()(ss ss ss ss ss ss ss s 强度条件强度条件 ssssssssss213232221)()()(21n4. 4. 畸变畸变能密度理论能密度理论（第四强度理论）（第四强度理论）实验表明：实验表明：对塑性材料，此理论比第三强度理对塑性