采样控制系统的分析

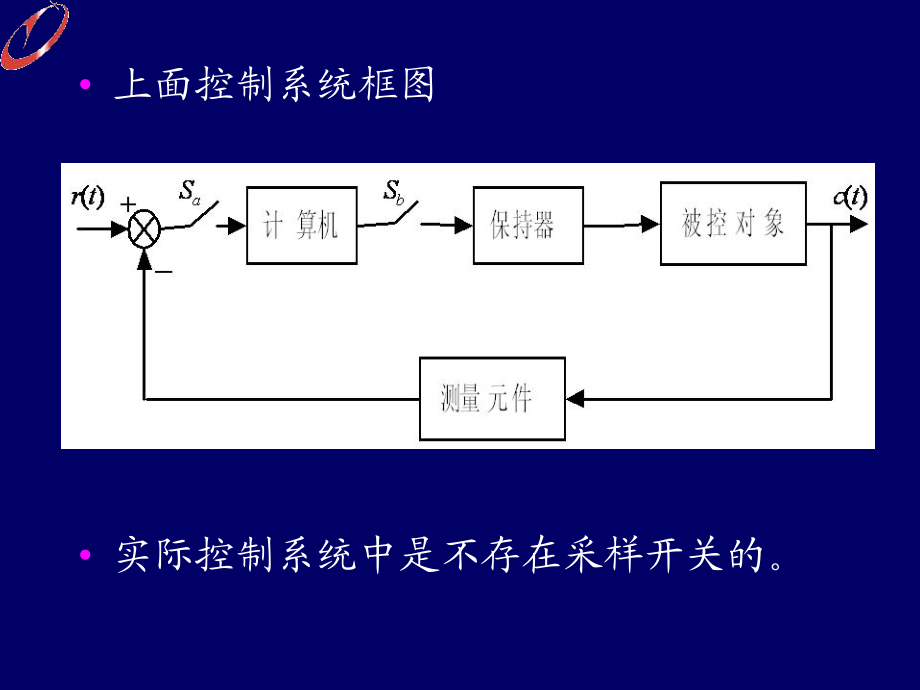
1、第第8 8章章 采样控制系统的分析与设采样控制系统的分析与设计计8-1 8-1 引言引言8-2 8-2 信号的采样与复现信号的采样与复现8-3 Z8-3 Z变换与变换与Z Z反变换反变换8-4 8-4 脉冲传递函数脉冲传递函数8-5 8-5 采样系统的分析采样系统的分析8-6 8-6 最少拍采样系统的校正最少拍采样系统的校正8-1 8-1 引言引言 前面各章分析了连续控制系统，这些系统中的前面各章分析了连续控制系统，这些系统中的变量是时间上连续的；变量是时间上连续的； 随着被控系统复杂性的提高，对控制器的要求随着被控系统复杂性的提高，对控制器的要求也越来越高，控制的成本随着数学模型的复杂也越来

2、越高，控制的成本随着数学模型的复杂化而急剧上升化而急剧上升模拟实现；模拟实现； 随着数字元件随着数字元件, ,特别是数字计算机技术的迅速特别是数字计算机技术的迅速发展，采样控制系统得到了广泛的应用；发展，采样控制系统得到了广泛的应用； 在采样控制系统中在采样控制系统中, ,有一处或多处的信号不是有一处或多处的信号不是连续信号连续信号, ,而在时间上是离散的脉冲序列或数而在时间上是离散的脉冲序列或数码码, ,这种信号称为采样信号。这种信号称为采样信号。典型的采样系统典型的采样系统 计算机直接数字控制系统计算机直接数字控制系统 上面控制系统框图 实际控制系统中是不存在采样开关的。 计算机控制系统的

3、优点：1、有利于实现系统的高精度控制；2、数字信号传输有利于抗干扰；3、可以完成复杂的控制算法，而且参数修 改容易；4、除了采用计算机进行控制外，还可以进行显示，报警等其它功能；5、易于实现远程或网络控制。 采样控制系统也是一类动态系统； 该系统的性能也和连续系统一样可以分为动态和稳态两部分； 这类系统的分析也可以借鉴连续系统中的一些方法，但要注意其本身的特殊性； 采样系统的分析可以采用Z变换方法，也可以采用状态空间分析方法。8-2 8-2 信号的采样与复现信号的采样与复现1 1、采样：、采样：把连续信号变成脉冲或数字序列的过把连续信号变成脉冲或数字序列的过程叫做采样；程叫做采样；2 2、采样

4、器：、采样器：实现采样的装置，又名采样开关；实现采样的装置，又名采样开关；3 3、复现：、复现：将采样后的采样信号恢复为原来的连将采样后的采样信号恢复为原来的连续信号的过程；续信号的过程；4 4、采样方式：采样方式： （1 1）等周期采样：）等周期采样： （2 2）多阶采样：采样是周期性重复的）多阶采样：采样是周期性重复的 （3 3）多速采样：有两个以上不同采样周期）多速采样：有两个以上不同采样周期的采样开关对信号同时进行采样的采样开关对信号同时进行采样 （4 4）随机采样：采样是随机进行的）随机采样：采样是随机进行的, ,没有固没有固定的规律定的规律 一个连续信号经采样开关变成了采样信号 采

5、样脉冲的持续时间远小于采样周期T和系统的时间常数 可以将窄脉冲看成是理想脉冲，从而可得采样后 的采样信号为1 1、信号的采样过程、信号的采样过程)()()(*tteteT tet0 teT te*0 te*t0TT2 *ett0TT2 是理想脉冲出现的时刻是理想脉冲出现的时刻因此采样信号只在脉冲因此采样信号只在脉冲出现的瞬间才有数值，出现的瞬间才有数值，于是采样信号变为于是采样信号变为 因此采样过程可以看作一个调制过程。因此采样过程可以看作一个调制过程。 kkTtt)()(kTkkTtkTete)()()(*0 tTtTT2T3T4T5采样信号的调制过程采样信号的调制过程 考虑到考虑到 时，时

6、，因此，可以将原来采样信号表达式变为如下因此，可以将原来采样信号表达式变为如下形式：形式：0t0)(te0*)()()(kkTtkTete将窄脉冲看作理想脉冲的条件是采样持续时间远远将窄脉冲看作理想脉冲的条件是采样持续时间远远小于采样周期和被控对象的时间常数小于采样周期和被控对象的时间常数2 2、采样定理、采样定理 由前面的分析可知，采样窄脉冲为周期性的，由前面的分析可知，采样窄脉冲为周期性的，采样后的信号采样后的信号 取该信号的拉氏变换取该信号的拉氏变换, ,并令并令 : : *1( )sjktke te t eT 说明采样后信号频谱是以说明采样后信号频谱是以 s s为周期的。为周期的。采样

7、时间满足什么条件？采样时间满足什么条件？才能复现原信号！才能复现原信号！ *1(j )jjskEEkT js 连续信号在时域上是连续的，但频域中的频谱是孤立的； 连续信号采样之后，具有以采样角频率 为周期的无限多个频谱。s 采样信号的频谱采样信号的频谱a )jEmaxmaxc ) (maxs2)j*Emaxmaxsb ) (maxs2)2s *jE maxmaxmax2s1K1K0K 1EsT 采样定理：采样定理：为使采样后的脉冲序列频谱互不搭为使采样后的脉冲序列频谱互不搭接，采样频率必须大于或等于原连续信号所含接，采样频率必须大于或等于原连续信号所含的最高频率的两倍，这样方可通过适当的理想的

8、最高频率的两倍，这样方可通过适当的理想滤波器把原信号毫无畸变的复现出来。滤波器把原信号毫无畸变的复现出来。 香农定理的物理意义是：香农定理的物理意义是：满足香农定理的采样满足香农定理的采样信号中含有连续信号的信息，该信息可以通过信号中含有连续信号的信息，该信息可以通过具有低通滤波特性的滤波器复现出来。具有低通滤波特性的滤波器复现出来。max2s3 3、零阶保持器、零阶保持器 保持器是采样系统的一个基本单元，功能是将保持器是采样系统的一个基本单元，功能是将采样信号恢复成连续信号。采样信号恢复成连续信号。 理想滤波器可以将采样信号恢复成连续信号；理想滤波器可以将采样信号恢复成连续信号； 理想滤波器

9、是物理上不可实现的，因此要寻找理想滤波器是物理上不可实现的，因此要寻找一种物理上可实现，特性上又接近于理想滤波一种物理上可实现，特性上又接近于理想滤波器的设备器的设备保持器。保持器。 采样信号只在采样点上有定义采样信号只在采样点上有定义, e, e* *(KT)(KT)和和e e* *(K+1)T)(K+1)T)都是有定义的都是有定义的, ,但是在这两者之间但是在这两者之间的时间段上连续信号应该是什么样子呢的时间段上连续信号应该是什么样子呢? ? 这就是保持器要解决的问题这就是保持器要解决的问题. . 保持器是一种时域外推装置，即将过去时刻或现在时保持器是一种时域外推装置，即将过去时刻或现在时

10、刻的采样值进行外推。刻的采样值进行外推。 通常把按照常数、线性函数和抛物线函数外推的保持通常把按照常数、线性函数和抛物线函数外推的保持器称为零阶、一阶和二阶保持器。器称为零阶、一阶和二阶保持器。 如果取如果取 则当前时刻的采样值将被保持到下一个采样时刻则当前时刻的采样值将被保持到下一个采样时刻. . 这种保持器称为零阶保持器这种保持器称为零阶保持器. . 如何用数学语言描述如何用数学语言描述这种特性呢这种特性呢? ? 2012eKTtaatat ,0e KTte KTtT 零阶保持器零阶保持器: :把采样时刻把采样时刻KTKT的采样值不增不的采样值不增不减地保持到下一个采样时刻（减地保持到下一

11、个采样时刻（K K1 1）T T。零阶保持器的输入和输出信号零阶保持器的输入和输出信号 sGh teT te* teh tet0a)b )c ) teht0TT2T3T4 te*t0TT2T3T4 由于在采样时刻由于在采样时刻 h,0,1,2ekTe kTk故保持器的输出故保持器的输出 h011kete kTtkTtkTT拉氏变换为拉氏变换为 h11eeTskTskEse kTss零阶保持器的传递函数为零阶保持器的传递函数为 hh*( )1 e( )TsEsGsE ss零阶保持器的传递函数为零阶保持器的传递函数为 零阶保持器的频率特性为零阶保持器的频率特性为 hh*( )1 e( )TsEsG

12、sE ssjjj22j2hj2j21 eeejej22 jesin(/2)sine22/2TTTTTTTGTTTTTTT 零阶保持器的频率特性如图所示零阶保持器的频率特性如图所示 零阶除了允许主频谱分量通过之外，还零阶除了允许主频谱分量通过之外，还允许一部分附加高频分量通过。因此复允许一部分附加高频分量通过。因此复现出的信号与原信号是有差别的。现出的信号与原信号是有差别的。jhGss3s2T023jhGjhG4 4、小结、小结 采样控制系统的结构；采样控制系统的结构； 计算机控制的采样系统的优点；计算机控制的采样系统的优点； 采样过程和采样定理；采样过程和采样定理； 零阶保持器的传函和特性。零

13、阶保持器的传函和特性。8-3 Z8-3 Z变换与反变换变换与反变换 线性连续控制系统线性连续控制系统可用可用线性微分方程线性微分方程来来描述，用描述，用拉普拉斯变换拉普拉斯变换分析它的暂态性分析它的暂态性能及稳态性能。能及稳态性能。 对于对于线性采样控制系统线性采样控制系统则可用则可用线性差分线性差分方程方程来描述，用来描述，用Z Z变换变换来分析它的暂态性来分析它的暂态性能及稳态性能。能及稳态性能。 Z Z变换是研究采样系统主要的数学工具，变换是研究采样系统主要的数学工具，由拉普拉斯变换引导出来，是采样信号由拉普拉斯变换引导出来，是采样信号的拉普拉斯变换。的拉普拉斯变换。 连续信号连续信号f

14、 f（t t）的拉普拉斯变换为）的拉普拉斯变换为 连续信号连续信号f f（t t）经过采样得到采样信号）经过采样得到采样信号 f f* *（t t）为）为 其拉普拉斯变换为其拉普拉斯变换为 定义新的变量定义新的变量 0)()(L)(dtetftfsFst0*)()()(kkTtkTftf0*)()()(kkTsekTftfLsFTsze 采样信号的采样信号的Z Z变换变换0*)()()(kkzkTftfZzF有有1 1、常用的、常用的Z Z变换方法变换方法 级数求和法：级数求和法：将采样信号将采样信号f f * *（t t）展开如下）展开如下对上式逐项进行拉普拉斯变换，得对上式逐项进行拉普拉斯

15、变换，得在一定条件下，常用函数的在一定条件下，常用函数的Z Z变换都能够写成闭合形式。变换都能够写成闭合形式。 *0( )() ()(0) ( )( ) ()() ()nftf nTtnTftf ttTf nTtnT *1( )(0)( )()( )(0)( )()TsnTsnFsff T ef nT eF zff T zf nT z【例【例1 1】求单位阶跃函数求单位阶跃函数1 1（t t）的）的Z Z变换。变换。 解：解： 单位阶跃函数的采样脉冲序列为单位阶跃函数的采样脉冲序列为 代入代入E(zE(z) )的级数表达式，得的级数表达式，得对上列级数求和，写成闭合形式，得对上列级数求和，写成

16、闭合形式，得 1,(0,1,2)e kTkL 1201e1kkkE zZte kTzzz LK11( )11zE zzz 部分分式法部分分式法1( )niiiAF ssp 当连续信号是以拉普拉斯变换式当连续信号是以拉普拉斯变换式F F（S S）的形式给出）的形式给出, ,且且F F（S S）为有理函数时）为有理函数时, ,可以展可以展开成部分分式的形式，即开成部分分式的形式，即 可得与其对应的可得与其对应的z z变换为变换为 由此可得由此可得F F（S S）的）的z z变换为变换为 iiAsp对应的时域表达式对应的时域表达式ip tiAeiipTzAze1( )inip TiAF zze【例【

17、例2 2】已知已知，试求其，试求其Z Z变换变换. . 解解 将将G G（s s）展开成部分分式）展开成部分分式 其对应的时域表示式为其对应的时域表示式为 两个时域信号的叠加两个时域信号的叠加 1(1)G ss s 11111E sG ss sss 1 ete t 1 e1e1e1eTtTTzzzE zZtzzzz 留数法留数法设连续信号设连续信号f(t)f(t)的拉普拉斯变换式的拉普拉斯变换式F F（S S）及其全部极点）及其全部极点p pi i为为已知，可利用留数法求其已知，可利用留数法求其Z Z变换变换F(z)F(z)，即，即 当当s=s=p pi i为一阶极点时，其留数为为一阶极点时，

18、其留数为 当当s=s=p pj j为为q q阶极点时，其留数为阶极点时，其留数为 s= s=p pi i处的留数处的留数 ()iiip TzRresFpze式中式中为为( )sTzF szelim ()()iiis TspzRspFsze111lim()( )(1)!iqjiqsTspdzRspF sqdsze*11( )( )()inniiP TiizFzZftresFpRze【例】求f（t）=t的z变换 t0 在在s=0s=0处有二阶极点，处有二阶极点，f(t)f(t)的的z z变换变换F(z)F(z)为为 解：解：由于由于21()Fss2200( )()(1)sTsTsTssdzzTeT

19、zF zRdszezez2 2、Z Z变换基本定理变换基本定理1.1.线性定理线性定理若若 i i为常数，则为常数，则 线性定理表明线性定理表明, ,时域函数线性组合的时域函数线性组合的z z变换等变换等于各时域函数于各时域函数z z变换的线性组合。变换的线性组合。 1122E zZ e ta Eza Ez L 1 122e ta eta etL 设有连续时间函数设有连续时间函数 2.2.滞后定理滞后定理 设设e(te(t) )的的z z变换为变换为E E（z z），且），且t t0 0时，时，e(te(t)=0,)=0,则则滞后定理说明，原函数在时域中延迟滞后定理说明，原函数在时域中延迟k

20、k个采样周期求个采样周期求z z变换变换, ,相当于它的相当于它的z z变换乘以变换乘以z z-k-k。因此。因此 z z-k-k可以表示可以表示时域中的滞后环节时域中的滞后环节, ,它把采样信号延迟它把采样信号延迟k k个采样周期个采样周期 nZ e tnTzE z tet tetnT3. 3. 超前定理超前定理4. 4. 初值定理初值定理 设函数设函数e(te(t) )的的z z变换为变换为E E(z(z) )，则，则 10nnkkZ e tnTzE ze kT z 0limlimtzetE z设设e(te(t) )的的z z变换为变换为 E E(z(z) )，而且，而且存在，则存在，则

21、0limtet5. 5. 终值定理终值定理 6 .6 .复数位移定理复数位移定理 1( )limlim1tzeetzE z 设函数设函数e(te(t) )的的z z变换为变换为E E(z(z) )，且，且在在z z平面上的以原点为圆心的单位平面上的以原点为圆心的单位圆上和圆外均圆上和圆外均没有极点，则没有极点，则 1zEz eeatatZ e tE zm设函数设函数e(te(t) )的的z z变换为变换为E(zE(z) )，则，则3 3、Z Z反变换反变换 由由E(zE(z) )求求e e* *(t)(t)过程称为过程称为z z反变换，表示为反变换，表示为 1e tZE z 由于由于z z变换

22、只表征连续函数在采样时刻的特性变换只表征连续函数在采样时刻的特性, ,并不反映采样时刻之间的特性并不反映采样时刻之间的特性, ,因此因此z z反变换只能求反变换只能求出采样函数出采样函数e e* *(t),(t),不能求出其连续函数不能求出其连续函数e(te(t) )。即有。即有 1ZEzete t常用的Z反变换方法1 1、长除法、长除法 将将E E( (z z) )的分子、分母多项式按的分子、分母多项式按z z的降幂形式排列的降幂形式排列, ,用分子多项式除以分母多用分子多项式除以分母多项式项式, ,可得到可得到E E( (z z) )关于关于z z-1-1的的无穷级数形式无穷级数形式, ,

23、在根据延迟定理得到在根据延迟定理得到e e* *(t)(t)。1010( )kkkkkE zee ze ze zLL对上式求对上式求z z反变换反变换, ,得得 *0( )()kke tetkT2 2、部分分式法、部分分式法 将将E(z)E(z)/z/z展开成部分分式。由于在展开成部分分式。由于在E(zE(z) )式中式中, ,分子分子表达式中通常含有表达式中通常含有z z。得到部分分式后。得到部分分式后, ,再将再将z z乘到各乘到各部分分式的分子部分部分分式的分子部分, ,再查表进行反变换即可再查表进行反变换即可, ,所以也所以也称为查表法。称为查表法。【例【例3 3】求求的的z z反变换

24、。反变换。 解解 将将E E (z)(z)/z/z展开成部分分式为展开成部分分式为 则对应的时间函数则对应的时间函数e e* *(t)(t)为为 1012zE zzz 1010101212E zzzzzz则有 101012zzE zzz 010etete TtTL0 10302703tTtTtTL3. 3. 留数法留数法由由z z变换的定义有变换的定义有 用用z zm-1m-1乘上式两端乘上式两端, ,得得 根据复变函数理论根据复变函数理论, ,知知 0kkE ze kT z 110mm kkE z ze kT z 1111dRe2 jiPmkizze kTE z zze kTs E z z

25、当当z=pz=pi i为单极点时，其留数为为单极点时，其留数为 当当z=pz=pj j为为n n重极点时，其留数为重极点时，其留数为 11Reslim () ( )iikkizzzzE z zzz E z z 1111d()( )1Reslim(1)!diinnkkinzzzzzzE z zE z znz4 4 差分方程差分方程 描述描述n n阶线性连续系统的数学模型为微分阶线性连续系统的数学模型为微分方程，而描述线性采样系统的教学方程，而描述线性采样系统的教学模型模型为为差分方程差分方程。 差分的定义：差分的定义： 一阶前向差分定义为一阶前向差分定义为 二阶前向差分定义为二阶前向差分定义为

26、1e ke ke k 211211221e ke ke ke ke ke ke ke ke ke ke ke ke k 一阶后向差分定义为：一阶后向差分定义为： 二阶后向差分定义为：二阶后向差分定义为： 1e ke ke k 2212e ke ke ke k tet ke ke1T1kk1k前向和后向差分示意图前向和后向差分示意图【例【例】 一阶采样系统的差分方程为一阶采样系统的差分方程为 解解: :对方程两边进行在对方程两边进行在z z变换，并由实移定理变换，并由实移定理 1y kby kr t其中其中b b为常数为常数, , ,00,kr kayy k求响应。 0zY zybY zR z

27、00kzr kaR zza，y因为因为 所以所以 zzb Y zza 11zYzZabbazbzazazb 1,(1, 2)kky kabkabL8-4 8-4 脉冲传递函数脉冲传递函数一、脉冲传递函数的基本概念一、脉冲传递函数的基本概念 线性采样系统初始条件为零时线性采样系统初始条件为零时, ,系统输出信号的系统输出信号的z z变换与输入信号的变换与输入信号的z z变换之比变换之比, ,称为线性采样系统的称为线性采样系统的脉冲传递函数脉冲传递函数, ,或简称为或简称为z z传递函数。传递函数。 实际采样系统的输出信号通常是连续信实际采样系统的输出信号通常是连续信号号, ,为了应用脉冲传递函数

28、为了应用脉冲传递函数概念概念, ,可在系统的可在系统的输出端虚设一个同步采样开关输出端虚设一个同步采样开关, ,使输出成为使输出成为采样信号。采样信号。 ( )( )( )Y zG zR z tr* sG tr ty ty* zG实际采样系统实际采样系统设输入脉冲序列为设输入脉冲序列为*0( )() ()kr tr kTtkT由叠加原理可求出系统对脉冲序列的响应为由叠加原理可求出系统对脉冲序列的响应为 ( )(0) ( )( ) ()() ()y trg tr T g t Tr nT g t nTLL根据根据z z变换的卷积定理，上式的变换的卷积定理，上式的z z变换为变换为 ( )( ) (

29、 )Y zG z R z 式中：式中：G(z)G(z)、R(z)R(z)、Y(zY(z) )分别为分别为g(t)g(t)、r(t)r(t)、y(ty(t) )的的z z变换。变换。 即采样系统脉冲传递函数即采样系统脉冲传递函数为为采样脉冲传函为连续系统的脉冲响应的采样脉冲传函为连续系统的脉冲响应的Z Z变换变换0( )( )()( )kkY zG zg kT zR z脉冲传递函数和连续系统的传递函数一样表脉冲传递函数和连续系统的传递函数一样表征了采样系统的固有特性；征了采样系统的固有特性；它除了与系统的结构、参数有关系，还与采它除了与系统的结构、参数有关系，还与采样开关在系统中的具体位置有关。

30、样开关在系统中的具体位置有关。1 1、两个环节有采样开关时、两个环节有采样开关时根据脉冲传递函数的定义：根据脉冲传递函数的定义：tr* sG1trty*1ty1 sG2ty*ty12( )( )( )( )( )Y zG zG z G zR z当环节之间有采样开关时，等效脉冲传递函数为各当环节之间有采样开关时，等效脉冲传递函数为各串联环节脉冲传递函数之积串联环节脉冲传递函数之积。该结论也可推广到。该结论也可推广到n n个个环节串联的情况环节串联的情况二、串联环节的脉冲传函二、串联环节的脉冲传函2 2、两个环节没有采样开关时、两个环节没有采样开关时)()()(2121zGzGzGGtr* sG1

31、tr sG2ty* ty当串联环节之间无采样开关时当串联环节之间无采样开关时, ,系统脉冲传递函数系统脉冲传递函数为各串联环节传递函数乘积的为各串联环节传递函数乘积的z z变换。该结论可推变换。该结论可推广到相互间无采样开关的广到相互间无采样开关的n n个环节串联的情况。个环节串联的情况。12( )( )( )( )Y zG zGG zR z3 3、有零阶保持器时的开环系统脉冲传递函数、有零阶保持器时的开环系统脉冲传递函数 a) tr* tr G s ty* ty h1 eTsG ssb) tr*1 tr ssG ty* tyeTs有零阶保持器时的开环采样系统有零阶保持器时的开环采样系统 三、

32、闭环系统的脉冲传递函数三、闭环系统的脉冲传递函数 tr ty* ty sG2 sH td te te* td* sG112( )( )( )( )( )( )E zR zB zB zE z GG H z12( )( )1( )R zE zGG H z121212( )( )( ) ( )( )1( )GGzY zGGz E zR zGG H z闭环系统的误差脉冲传递函数闭环系统的误差脉冲传递函数 12( )1( )( )1( )eE zG zR zGG H z闭环系统脉冲传递函数闭环系统脉冲传递函数为为12B12( )( )( )( )1( )G GzY zGzR zG G H z系统输出系统

33、输出当系统有扰动作用时当系统有扰动作用时 , ,可得闭环系统的误差与扰动间可得闭环系统的误差与扰动间的脉冲传递函数为的脉冲传递函数为 212( )( )( )1( )G H zE zD zGG H z 系统输出与扰动之间系统输出与扰动之间的脉冲传递函数的脉冲传递函数 122212( )( )( )( )( )1( )GG z G H zY zG zD zGG H z由于系统中有采样器的存在，由于系统中有采样器的存在，所以一般情况下所以一般情况下 ( )( )1( )1( )G zG sZG zG s例例 设闭环采样系统结构图如图所示，试设闭环采样系统结构图如图所示，试证其闭环脉冲传递函数为证其

34、闭环脉冲传递函数为 12B12( )( )( )1( )( )G z GzGzG z HGz tr ty* ty sG1 sG2 sH sE sE* sE1 sE*1闭环采样系统结构图闭环采样系统结构图 对于有些采样控制系统，无法写出闭环脉冲传递函数只能写出输出的Z变换 sG sY sH sR sG1 sYsH sRsG2 1RG zY zHG z 12121RGz GzY zGG H z8-5 8-5 采样系统的分析采样系统的分析 稳定性分析稳定性分析 闭环极点分布与瞬态响应的关系闭环极点分布与瞬态响应的关系 稳态误差分析稳态误差分析1 1、采样稳定性分析、采样稳定性分析1 1）稳定性的基本

35、概念）稳定性的基本概念 稳定性是指在扰动的作用下，系统会偏稳定性是指在扰动的作用下，系统会偏离原来的平衡位置，在扰动撤除后，系离原来的平衡位置，在扰动撤除后，系统恢复到原来平衡状态的能力；统恢复到原来平衡状态的能力； 根据稳定性的定义，可以采用脉冲响应根据稳定性的定义，可以采用脉冲响应的情况来研究系统的稳定性；的情况来研究系统的稳定性； 系统的脉冲响应如果能够衰减到系统的脉冲响应如果能够衰减到0 0，则系，则系统是稳定的；统是稳定的； 否则系统是不稳定的。否则系统是不稳定的。 采样系统的脉冲响应： 由Z反变换得 由上式可若 ，即系统的所有极点位于Z平面的单位圆内，则1( )( ) ( )( )

36、niiiA zY zT z R zT zzz 1)(zR11( )nkiiiy kA z nizi, 2 , 1, 10lim11nikiikzA2 2）稳定条件：）稳定条件：采样系统稳定的充分必要条件是：采样系统稳定的充分必要条件是： 系统闭环脉冲传递函数的所有极点位于系统闭环脉冲传递函数的所有极点位于Z Z平面上的单位圆内。或者说，所有极点的模都平面上的单位圆内。或者说，所有极点的模都小于小于1,1,即即 ，单位圆就是稳，单位圆就是稳定区域的边界。定区域的边界。1,(1,2,)iiL S平面的左半平面 ，z的幅值在0和1之间变化，对应z平面单位圆内； S平面的虚轴 ，对应z平面的单位圆；

37、当 由 变到 时，jsezTs,sTTzez2arg,00z2s2s3 3）s s平面与平面与z z平面的映射关系平面的映射关系 线性采样系统不能直接使用劳斯稳定判线性采样系统不能直接使用劳斯稳定判据，因为采样系统稳定边界是据，因为采样系统稳定边界是z z平面上以平面上以原点为圆心的单位圆周，而不是虚轴。原点为圆心的单位圆周，而不是虚轴。为能使用劳斯判据，可将为能使用劳斯判据，可将z z平面上单位圆平面上单位圆周映射到新坐标系中的虚轴，这种变换周映射到新坐标系中的虚轴，这种变换称为称为w w变换变换，或称双线性变换。，或称双线性变换。4 4）线性采样系统劳斯判据）线性采样系统劳斯判据式中，式中

38、，z z、w w均为复变量，可分别写为均为复变量，可分别写为 代入双线性变换公式，得代入双线性变换公式，得w w平面虚轴上的点对应于平面虚轴上的点对应于上式中实部为零的点，即上式中实部为零的点，即 则则11zzw设设11wzw jjzxy w uv ，22222212jj(1)(1)xyyuvxyxy22221(1)xyuxy z z平面上单位圆内平面上单位圆内(x(x2 2+y+y2 21)1)对应着对应着w w平面实部平面实部为负数的左半平面。为负数的左半平面。z z平面上单位圆外平面上单位圆外(x(x2 2+y+y2 21)1)对应着对应着w w平面实部为正数的右半平面。平面实部为正数的

39、右半平面。z z平面平面与与w w平面的映射平面的映射关系所示。关系所示。uju平面wz平面xy j【例【例】设采样控制系统的方框图如图所示。设采样控制系统的方框图如图所示。采样周期采样周期T=1s, T=1s, T=0.5sT=0.5s试求使系统稳定试求使系统稳定的的K K值范围。值范围。 解解 系统的开环脉冲传递函数为系统的开环脉冲传递函数为 sR sYT1ssK1 eTss12(e1)(1 ee )( )1(1)(1)(e )TTTTKTzTG zzZKs szz 相应的闭环系统特征方程相应的闭环系统特征方程为为 10D zG z 将将T=1sT=1s代入上式，得代入上式，得 进行进行w

40、 w变换可求得变换可求得w w域系统的特征方程为域系统的特征方程为 2( )(0.3681.368)(0.2640.368)0D zzKzK2( ) 0.632(1.264 0.528 )(0.2640.368) 0D wKwK wK根据代数判据，闭环系统稳定条件根据代数判据，闭环系统稳定条件为为1.2640.5280K所以稳定时所以稳定时K K的取值为的取值为 02.4K同理可得同理可得T=1sT=1s时时 稳定时稳定时K K的取值为的取值为 02.4K稳定时稳定时K K的取值为的取值为 同理可得同理可得,T=0.5s,T=0.5s时时 04.37K开环增益开环增益K K和采样周期和采样周期

41、T T对采样系统稳定性有如下影响：对采样系统稳定性有如下影响：(1)(1)采样周期采样周期T T一定时，增加开环增益一定时，增加开环增益K K会使采样系统稳定会使采样系统稳定性变差，甚至使系统不稳定。性变差，甚至使系统不稳定。(2)(2)开环增益开环增益K K一定时一定时, , 采样周期采样周期T T越长，丢失的信息越多，越长，丢失的信息越多，对采样系统稳定性及动态性能均不利，甚至使系统不稳定。对采样系统稳定性及动态性能均不利，甚至使系统不稳定。2、闭环脉冲传递函数零、极点分布与闭环脉冲传递函数零、极点分布与暂态响应的一般关系暂态响应的一般关系 1）系统的单位阶跃响应 设闭环采样系统的脉冲传递

42、函数为设闭环采样系统的脉冲传递函数为式中式中M M(Z)(Z)、D(Z)D(Z)闭环脉冲传递函数分子闭环脉冲传递函数分子多项式和分母多项式多项式和分母多项式 设设 i i闭环极点闭环极点 z zj j闭环零点闭环零点1011B1011( )( )( )( )( )mmmmnnnnb zb zbzbY zM zGzR za za zazaD zLL当输入为单位阶跃信号时系统输出信号的z变换为 10110121()( )( ) ( )( )11()()()mmmmBBnb zb zbzbazzY zGz R zGzzzzzzLL( )1zR zz将上式展成部分分式可得01( )1niiizzY z

43、AAzz式中：01()( ),( )(1)()iiiizMMzAAD zD对上式进行对上式进行z z反变换，得采样系统输出采样信号为反变换，得采样系统输出采样信号为 上式右边第一项为系统的稳态响应分量，第二项上式右边第一项为系统的稳态响应分量，第二项为暂态响应分量。为暂态响应分量。01( )1( )nkiiiy kAkA 显然,随极点在平面位置的不同，它所对应的暂态分量也不同。 实数极点：实数极点：若实数极点分布在单位圆内，其对应的若实数极点分布在单位圆内，其对应的分量呈衰减变化。正实数极点对应的单调衰减，负分量呈衰减变化。正实数极点对应的单调衰减，负实数极点对应的振荡衰减；实数极点对应的振荡

44、衰减； 共轭极点：共轭极点： 有一对共轭复数极点有一对共轭复数极点 i i与与 i i，即，即 jje,e( )2cos()iiiiiikiiiiiy kAk当当| | i i| |1 1时时,y,yi i(k(k) )为发散振荡函数；当为发散振荡函数；当| | i i| |1 1时，时，y yi i(k(k) )为衰减振荡函数为衰减振荡函数, ,振荡角振荡角频率为频率为 i i为共轭复数系数为共轭复数系数A Ai i的幅角。的幅角。 iiT xxxxxx暂态响应与极点位置关系暂态响应与极点位置关系 1)1)当闭环脉冲传递函数的极点位于当闭环脉冲传递函数的极点位于z z平面上以平面上以原点为圆

45、心的单位圆内时原点为圆心的单位圆内时, ,其对应的暂态分量其对应的暂态分量是衰减的。是衰减的。 2)2)要使控制系统具有比较满意的暂态响应要使控制系统具有比较满意的暂态响应, ,其其闭环极点应尽量避免分布在闭环极点应尽量避免分布在Z Z平面单位圆平面单位圆内内的的左左半部半部, ,最好分布在单位圆内的右半部。最好分布在单位圆内的右半部。 3)3)极点尽量靠近坐标原点极点尽量靠近坐标原点, ,相应的暂态分量衰相应的暂态分量衰减速度较快。减速度较快。 4)4)离单位圆周最近且附近无闭环零点的共轭复离单位圆周最近且附近无闭环零点的共轭复数极点为主导极点。数极点为主导极点。3 3、采样系统的稳态误差、

46、采样系统的稳态误差 与连续系统类似地求稳态误差有两种方与连续系统类似地求稳态误差有两种方法：法： 1)1)应用应用z z变换变换终值定理终值定理计算稳态误差的终计算稳态误差的终值；值； 2)2)应用误差脉冲传递函数计算应用误差脉冲传递函数计算静态误差静态误差系数系数, ,进而进而得到稳态误差。得到稳态误差。 误差脉冲传递函数为误差脉冲传递函数为 tr ty* ty te te* zG( )( )1( )R zE zG z闭环采样控制系统闭环采样控制系统 由由z z变换终值定理得稳态误差为变换终值定理得稳态误差为 与连续系统类似与连续系统类似, ,开环脉冲传递函数的一般开环脉冲传递函数的一般形式

47、为形式为11( )lim ( )lim(1) ( )lim(1)1( )sskzzR zee kzE zzG z 11()( )(1)()mjjn vviiKzzG zzzp =0=0称为称为0 0型系统；型系统； =1=1称为称为I I型系统；型系统； =n=n称为称为n n型系统。型系统。定义为静态位置误差系数定义为静态位置误差系数对于对于0 0型系统型系统 为一常量，稳态误差为为一常量，稳态误差为对于对于型及以上系统型及以上系统( )1r t ( )1zR zz 11111lim (1)lim1( )11(1)sszzpzezG zzGK 1lim 1( )pzKG zpK1sspeK

48、pK0sse1 1）单位阶跃输入：）单位阶跃输入：定义静态速度误差系数定义静态速度误差系数对于对于0 0型系统型系统 ，稳态误差为，稳态误差为对于对于型型 为常值为常值 , , 也为常值也为常值对于对于型及以上系统型及以上系统0vKsse0ssevKssevK22111( )(1)111( )lim (1)limlim1( ) (1)(1)1( )(1) ( )zzzvTzR zzTzTezTTG zzzG zzG zK 1lim(1) ( )vzKzG z2 2）单位斜坡输入：）单位斜坡输入：定义静态加速度误差系数对于0型和型系统 ，稳态误差为对于型 为常值, 也为常值0vKssevKsse

49、23222211(1)( )2(1)1(1)1( )lim(1)lim1( ) 2(1)(1)( )zzT z zR zzT z zezTG zzzG z 21lim(1)( )azKzG z3 3）单位加速度输入：）单位加速度输入： 采样系统误差除了与系统的结构、参数和输入信采样系统误差除了与系统的结构、参数和输入信号有关外，还与采样周期有关，缩小采样周期可号有关外，还与采样周期有关，缩小采样周期可以减小稳态误差。以减小稳态误差。系统型别系统型别位置误差位置误差速度误差速度误差加速度误差加速度误差0 0型型1 1型型0 02 2型型0 00 01pKvTK2aTK例例 采样系统结构图如图所示

50、，设采样系统结构图如图所示，设T=0.2sT=0.2s，输入信号为，输入信号为求系统的稳态误差。求系统的稳态误差。21( )12r ttt tr tyT te te*215 . 010ss1eTss解：解： 系统的开环脉冲传递函数为系统的开环脉冲传递函数为2133210(0.51)1 5(1)5( )(1)(1)(1)szT z zTzG zzZszzz解：解： 系统的开环脉冲传递函数为系统的开环脉冲传递函数为2133210(0.51)1 5(1)5( )(1)(1)(1)szT z zTzG zzZszzzT=0.2sT=0.2s时时21.20.8( )(1)zG zz系统特征方程为系统特征

51、方程为 20.80.20zz1,20.4j0.2所以系统稳定所以系统稳定 ,0.4pvaKKK 所以采样时刻的稳态误差为所以采样时刻的稳态误差为 21( )0.1pvaTTeKKK 关于采样时刻之间的波纹引起的误差关于采样时刻之间的波纹引起的误差 0TT2T3T4T5)(tyt由于采样，系统中增加由于采样，系统中增加了高频分量，造成了采了高频分量，造成了采样间隔的纹波如图所示。样间隔的纹波如图所示。它们同样影响到采样点它们同样影响到采样点的稳态误差，所以在用的稳态误差，所以在用上述方法求误差时，严上述方法求误差时，严格说还应将它们也考虑格说还应将它们也考虑进去。分析纹波须应用进去。分析纹波须应

52、用修正修正z z变换法。变换法。 采样时刻间的纹波采样时刻间的纹波 8-6 8-6 最少拍采样系统的校正最少拍采样系统的校正 在采样系统中通常将一个采样周期称之为一拍，在采样系统中通常将一个采样周期称之为一拍，若在典型输入信号作用下，经过最少采样周期，若在典型输入信号作用下，经过最少采样周期，系统的采样误差信号减小为零实现完全跟踪，系统的采样误差信号减小为零实现完全跟踪，则称之为则称之为最少拍系统最少拍系统。 sR sY sE zD sGh sG0TT具有数字控制器的采样控制系统具有数字控制器的采样控制系统 闭环脉冲传递函数闭环脉冲传递函数 B( )( ) ( )( )( )1( ) ( )Y

53、 zD z G zGzR zD z G z误差脉冲传递函数为误差脉冲传递函数为( )1( )( )1( ) ( )EE zGzR zD z G z( )1( )BEGzGz 且求出数字控制器的脉冲传递函数为求出数字控制器的脉冲传递函数为 B( )( )( ) 1( )BGzD zG zGz或或 1( )( )( )( )EEGzD zG z Gz 最小拍系统的设计是针对典型输入作用进行的最小拍系统的设计是针对典型输入作用进行的. . 典型输入信号的典型输入信号的z z变换可以表示为如下一般形式变换可以表示为如下一般形式1( )( )(1)A zR zz所以有所以有 1( )( )( ) ( )( )(1)EEA zE zGz R zGzz根据终值定理，采样系统的稳态误差为根据终值定理，采样系统的稳态误差为 11111( )( )lim(1) ( )lim(1)( )(1)EzzA zezE zzGzz 根据终值定理，采样系统的稳态误差为根据终值定理，采样系统的稳态误差为 11111( )( )lim(1) ( )lim(1)( )(1)EzzA zezE zzGzz 要使系统无稳态误差要使系统无稳态误差 1( )(1)( )EGzzF