5平行线的性质定理

1、授课人修世刚备课时间3.26上课时间4.2执教班级7.6课题平行线的性质定理教学课时1教学课题、实验等复习、1新授课-|教学 目标一教学知识点1平行线的性质定理的证实.2证实的一般步骤.二水平练习要求1.经历探索平行线的性质定理的证实.培养学生的观祭、分析和进行 简单的逻辑推理水平.2结合图形用符号语言来表示平行线的三条性质的条件和结论并能总结归纳出证实的一般步骤.三情感与价值观要求通过师生的共同活动,培养学生的逻辑思维水平,熟悉综合法证实 的格式.进而激发学生学习的积极主动性.教学 重点、难点一重点在观察实验的根底上进行公理的概括与定理的推导.二难丿点 推理过程的标准化表达.媒体运 用电子白

2、板预设过程应包括课程导入、预习自学、展示交流、当堂练习检测等I 巧设现实情境,引入新课师上节课我们通过推理得证了平行线的判定定理,知道它们的条件是角的大小关系.其结论是两直线平行.如果我们把平行线的判定定理的条件和结论互 换之后得到的命题是真命题吗？这节课我们就来研究“如果两条直线平行.II 讲授新课师在前一节课中,我们知道：“两条平行线被第三条直线所截,同位角 相等这个真命题是公理,这一公理可以简单说成：两直线平行,同位角相等.下面大家来分组讨论议一议：利用这个公理,你能证实哪些熟悉的结论？生甲利用“两条直线平行,同位角相等可以证实：两条直线平行,内 错角相等.生乙还可以证实：两条直线平行,

3、同旁内角互补 .师很好下面大家来想一想：(1) 根据“两条平行线被第三条直线所截,内错角相等你能作出相关的 图形吗？(2) 你能根据所作的图形写出、求证吗？生甲根据上述命题的文字表达,可以作出相关的图形如图1.生乙由于“两条平行线被第三条直线所截,内错角相等这个命题的条 件是：两条平行线被第三条直线所截.它的结论是：内错角相等所以我根据所作 的图形如图1,把这个文字命题改写为符号语言即：,如图1,直线a/ b,Z 1和/2是直线a、b被直线c截出的内错角.求证：/ 1 = 2 2.师乙同学表达得很好.投影片为上面的符号语言你能说说证实的思路吗？生丙要证实内错角21 = 2 2,从图中知道2 1

4、与2 3是对顶角所以2仁2 3,由此可知：只需证实2 2=2 3即可而2 2与2 3是同位角这样可根据平行线 的性质公理得证.师丙同学的思路清楚我们来根据他的思路书写证实过程.哪位同学上黑 板来书写呢？学生举手,请一位同学来生丁证实：T a / b 2 3=2 2 两直线平行,同位角相等T2 1=2 3 对顶角相等 2 1=2 2 等量代换师同学们写得很好通过证实证实了这个命题是真命题, 我们可以把它称 为定理即平行线的性质定理这样就可以把它作为今后证实的依据.注意：1随堂练习和习题中用黑体字给出的结论也可以作为今后证实的依 据所以像“对顶角相等就可以直接应用.2这个性质定理的条件是：直线平行

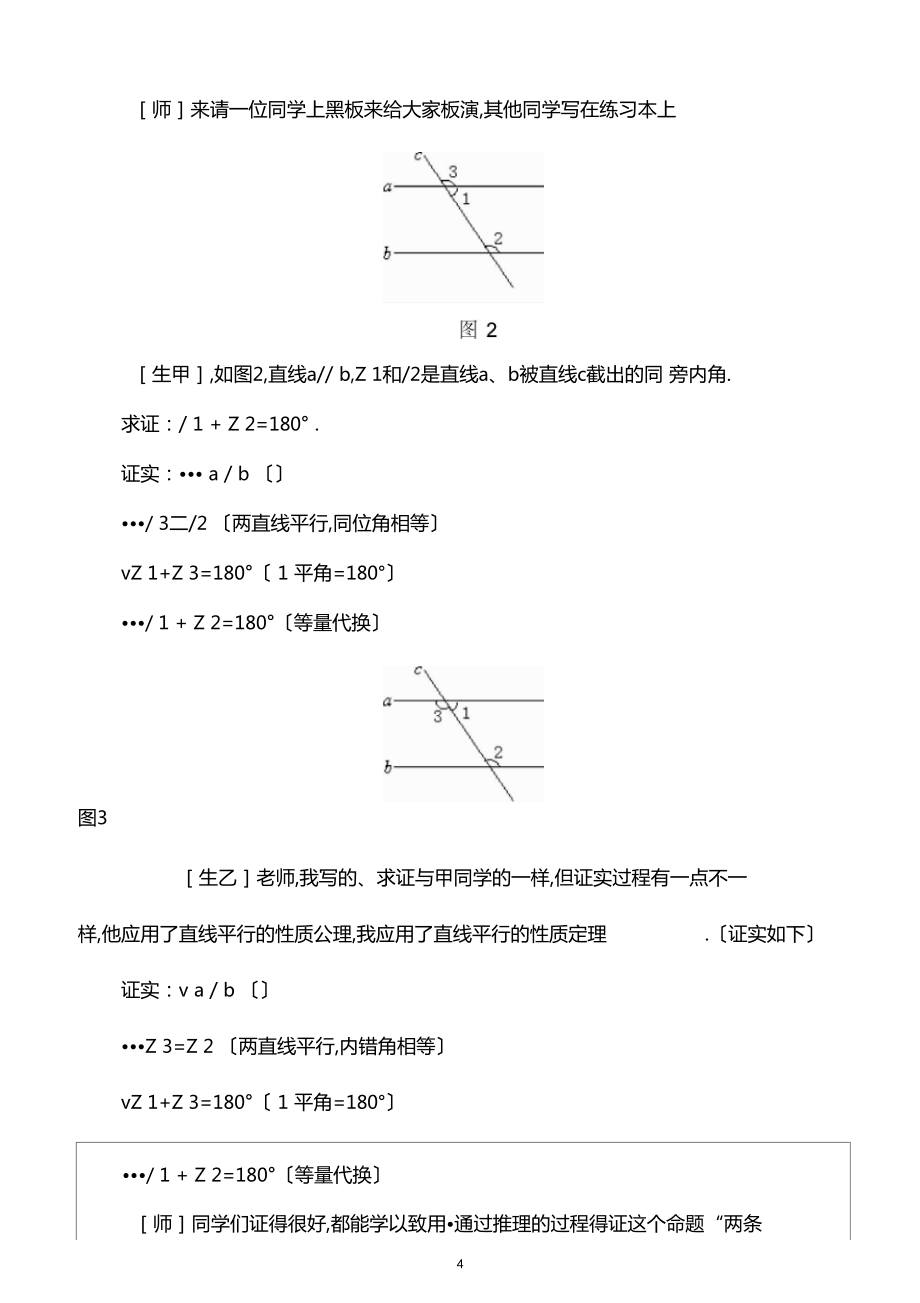
5、结论是：角的关系在应用时一定要接下来我们来做一做由判定公理可以证实的另一命题两条平行线被第三条直线所截,同旁内角互补.师来请一位同学上黑板来给大家板演,其他同学写在练习本上生甲,如图2,直线a/ b,Z 1和/2是直线a、b被直线c截出的同 旁内角.求证：/ 1 + Z 2=180° .证实： a / b / 3二/2 两直线平行,同位角相等vZ 1+Z 3=180° 1 平角=180°/ 1 + Z 2=180°等量代换图3生乙老师,我写的、求证与甲同学的一样,但证实过程有一点不一样,他应用了直线平行的性质公理,我应用了直线平行的性质定理.证实如下证实

6、：v a / b Z 3=Z 2 两直线平行,内错角相等vZ 1+Z 3=180° 1 平角=180°/ 1 + Z 2=180°等量代换师同学们证得很好,都能学以致用通过推理的过程得证这个命题“两条 平行线被第三条直线所截,同旁内角互补是真命题我们把它称为定理,即直线 平行的性质定理,以后可以直接应用它来证实其他的结论 .到现在为止,我们通过推理得证了两个判定定理和两个性质定理,那么你能 说说证实的一般步骤吗？大家分组讨论、归纳 .师生共析好,我们来共同归纳一下证实的一般步骤：第一步：根据题意,画出图形.先根据命题的条件即事项,画出图形,再把命题的结论即求证的内

7、容在 图上标出符号,还要根据证实的需要在图上标出必要的字母或符号,以便于表达 或推理过程的表达.第二步：根据条件、结论,结合图形,写出、求证 .把命题的条件化为几何符号的语言写在中,命题的结论转化为几何符号 的语言写在求证中.第三步,经过分析,找出由推出求证的途径,写出证实过程一般情况下,分析的过程不要求写出来,有些题目中,已经画出了图形,写好了、求证,这时只要写出“证实 一项就可以了 .师接下来我们来做一练习,以进一步稳固证实的过程 .皿.课堂练习一补充练习图41证实相邻的补角的平分线互相垂直.：如图4, / AOB、/ BOC互为邻补角,0E平分/ AOB, OF平分/ BOC.求证：0E

8、丄OF.证实：T OE平分/ AOB.OF平分/ BOC / EOB=二看课本,然后小结IV.课时小结这节课我们主要研究了平行线的性质定理的证实,总结归纳了证实的一般步骤.1平行线的性质：公理：两直线平行,同位角相等定理：两直线平行,内错角相等定理：两直线平行,同旁内角互补2证实的一般步骤 根据题意,画出图形. 根据条件、结论,结合图形,写出、求证 . 经过分析,找出由推出求证的途径,写出证实过程. / AOB2/ BOF= 1 / BOC 角平分线定义2/ AOB+ / BOC=180° 1 平角=180° / EOB+ / BOF=； / AOB+ / BOC =90.

9、等式的性质即/ EOF=90° 0E丄OF 垂直的定义V .课后作业一课后习题二1预习后面的内容2预习提纲1三角形的内角和定理是什么?2三角形的内角和定理的证实W.活动与探究图51.,如图 5, AB/ CD,/ B= / D,求证：AD / BC.过程让学生在证实这个题时,可从多方面考虑,从而拓展了他们的思维, 要证：AD / BC,可根据平行线的五种判定方法,结合图形,可证同旁内角互补, 内错角相等,同位角相等.结果证法一：T AB/ DC /B+ / C=180 ° 两直线平行,同旁内角互补V/ B= / D / D+ / C=180° 等量代换二AD / BC 同旁内角互补,两直线平行图6证法二：如图6,延长BA 构造一组同位角vAB/ CD /仁/ D 两直线平行,内错角相等v/ B= / D / 1 = / B 等量代换 AD / BC 同位角相等,两直线平行图7证法三：如图7,连接BD 构造一组内错角v AB / CD /仁/4 两直线平行,内错角相等v/ B= / D / B/仁/D / 4 等式的性质 / 2=/ 3 AD / BC 内错角相等,两直线平行平行线的性质定理板书 设计1.公理：两直线平行,同位角相等2定理：两直线平行,内错角相等3定理：两直线平行,同旁内角互补教学后记或反思主要记录课堂设计理念,实际教