勾股定理第一节

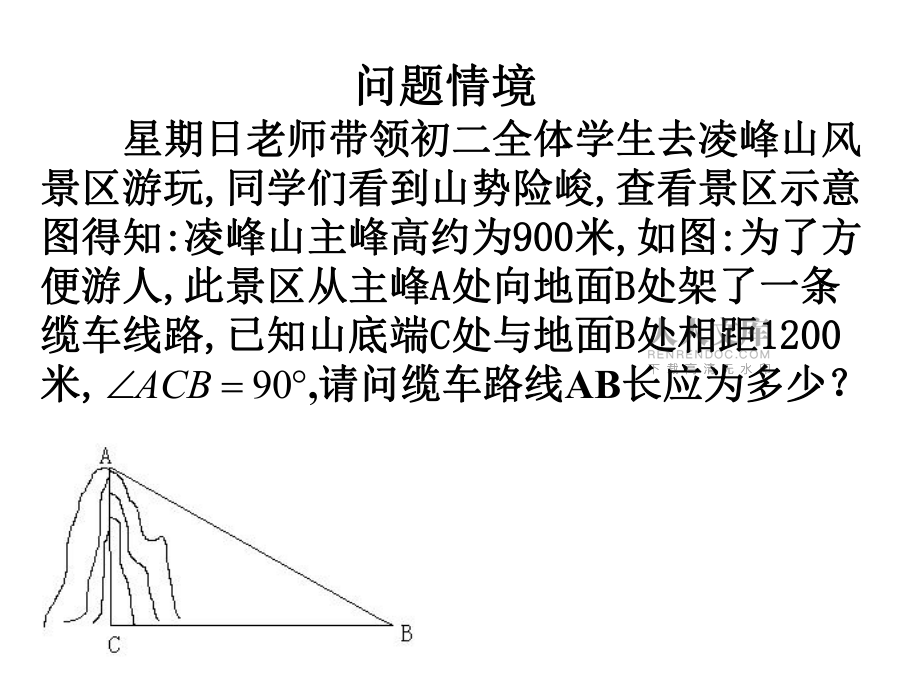
1、.历史因你而改变历史因你而改变 学习因你而精彩学习因你而精彩 勾股定理勾股定理. 星期日老师带领初二全体学生去凌峰山风星期日老师带领初二全体学生去凌峰山风景区游玩景区游玩, ,同学们看到山势险峻同学们看到山势险峻, ,查看景区示意查看景区示意图得知图得知: :凌峰山主峰高约为凌峰山主峰高约为900900米米, ,如图如图: :为了方为了方便游人便游人, ,此景区从主峰此景区从主峰A A处向地面处向地面B B处架了一条处架了一条缆车线路缆车线路, ,已知山底端已知山底端C C处与地面处与地面B B处相距处相距12001200米米, , ,请问缆车路线请问缆车路线AB长应为多少？长应为多少？90A

2、CB问题情境问题情境.1了解勾股定理的发现过程，掌握勾股定了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理。理的内容，会用面积法证明勾股定理。2培养在实际生活中发现问题总结规律的培养在实际生活中发现问题总结规律的意识和能力。意识和能力。3介绍我国古代在勾股定理研究方面所取介绍我国古代在勾股定理研究方面所取得的成就，激发爱国热情，勤奋学习。得的成就，激发爱国热情，勤奋学习。重点：勾股定理的内容及证明。重点：勾股定理的内容及证明。难点：勾股定理的证明。难点：勾股定理的证明。.（一）、课前准备（一）、课前准备（2 2分钟）分钟）1 1、直角、直角ABCABC的主要性质是：的主要性质

3、是：C=90C=90（用几何（用几何语言表示）语言表示）1）两锐角之间的关系： ；2）若若B=30，则，则B的对边和斜边：的对边和斜边： ACBD.看一看看一看 相传两千五百年前，一次毕达相传两千五百年前，一次毕达哥拉斯去朋友家作客，发现朋友家哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们边的某种数量关系，同学们，我们也来观察一下图案，看看你能发现也来观察一下图案，看看你能发现什么？什么？.ABC你能发现图中的等腰直角三角形有什你能发现图中的等腰直角三角形有什么性质吗？么性质吗？等腰直角三角形：斜边的平方等于两条直等腰直

4、角三角形：斜边的平方等于两条直角边的平方和。角边的平方和。.在等腰直角三角形中斜边的平方等于两条在等腰直角三角形中斜边的平方等于两条直角边的平方和，其他的直角三角形中也直角边的平方和，其他的直角三角形中也有这个性质吗？有这个性质吗？一般的直角三角形三边关系一般的直角三角形三边关系（二）总结规律，大胆才猜想（二）总结规律，大胆才猜想（5分钟）分钟）.A AB BC Ca ac cb bS SA A+S+SB B=S=SC C如果直角三角形的两条直角如果直角三角形的两条直角边长分别是边长分别是a、b，斜边长斜边长为为c.猜想猜想:两直角边两直角边a、b与斜边与斜边c 之间的关系？之间的关系？a a

5、2 2+b+b2 2=c=c2 2结论：结论：直角三角形中，两条直角边的平方和，直角三角形中，两条直角边的平方和，等于斜边的平方等于斜边的平方. .如果直角三角形两直角边分别为如果直角三角形两直角边分别为a，b，斜边为，斜边为c，那么，那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方即直角三角形两直角边的平方和等于斜边的平方.勾股定理勾股定理cab勾勾股股弦弦 C C9090 a2 + b2 = c2. 读一读读一读 我国古代把直角三角形中较短的直角边称为勾，我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦较长的直角边称为股，斜边称为弦.图图1-1

6、称为称为“弦图弦图”，最早是由三国时期的数学家赵爽在为周髀算经，最早是由三国时期的数学家赵爽在为周髀算经作法时给出的作法时给出的.图图1-2是在北京召开的是在北京召开的2002年国际数年国际数学家大会（学家大会（TCM2002）的会标，其图案正是的会标，其图案正是“弦图弦图”，它标志着中国古代的数学成就，它标志着中国古代的数学成就. 图1-1图1-2.（三）勾股定理的证明（三）勾股定理的证明 ab4+(b-a)=c a+b =cabc2ab+（b-2ab+a）=c12【证法【证法1 1】.abcabcbcabcaabaaabbbccS=1/2ab4+ c=1/2ab 4+ a+b a+b =c

7、【证法证法2】已知：在已知：在ABC中，中，C=90，A、B、C的对边为的对边为a、b、c。求证：求证：a2b2=c2 .【 证法证法3 3】（】（18761876年美国总统年美国总统Garfield证证明明）以以a、b 为直角边，以为直角边，以c为斜边作两为斜边作两个全等的直角三角形，则每个直角个全等的直角三角形，则每个直角三角形的面积等于三角形的面积等于ab. 把这两个直把这两个直角三角形拼成如图所示形状，使角三角形拼成如图所示形状，使A、E、B三点在一条直线三点在一条直线上. bcabcaADCD.美国总统证法：美国总统证法：bcabcaADCDS梯形梯形ABCD=1/2(a+b)(a+

8、b) =1/2ab2+1/2 ca+b =c.分析：已知分析：已知ABC中，中，90ACB， AC=900米，米，BC=1200米米， 求斜边求斜边ABAB的长的长. 例：例：星期日老师带领初二全体学生去凌峰山风景区游玩星期日老师带领初二全体学生去凌峰山风景区游玩,同学们看到山势险峻同学们看到山势险峻,查看景区示意图得知查看景区示意图得知:凌峰山主峰高凌峰山主峰高约为约为900米米,如图如图:为了方便游人为了方便游人,此景区从主峰此景区从主峰A处向地面处向地面B处架了一条缆车线路处架了一条缆车线路,已知山底端已知山底端C处与地面处与地面B处相距处相距1200米米,请问缆车路线请问缆车路线AB长

9、应为多少长应为多少? 90ACB三、应用定理三、应用定理 巩固新知巩固新知.四、随堂练习 1、如图，直角ABC的主要性质是：C=90，（用几何语言表示） 两锐角之间的关系： ； (2)若B=30，则B的对边和斜边： ； (3)三边之间的关系： ACBD.五.课堂检测 1、在RtABC中，C=90 若a=5，b=12，则c=_； 若a=15，c=25，则b=_； 若c=61，b=60，则a=_； 若a b=3 4，c=10则SRtABC =_。. 2、已知在RtABC中，B=90，a、b、c是ABC的三边，则 c= 。（已知a、b，求c） a= 。（已知b、c，求a）. 3、直角三角形两直角边长

10、分别为5和12，则它斜边上的高为_。 4、.已知一个Rt的两边长分别为3和4，则第三边长的平方是（） A、25 B、14C、7D、7或25 5、等腰三角形底边上的高为8，周长为32，则三角形的面积为（） A、56B、48C、40D、32.、本节课我们经历了怎样的过程？、本节课我们经历了怎样的过程？经历了从实际问题引入数学问题然后发现定理，再到探经历了从实际问题引入数学问题然后发现定理，再到探索定理，最后学会验证定理及应用定理解决实际问题的过程索定理，最后学会验证定理及应用定理解决实际问题的过程.、本节课我们学到了什么？、本节课我们学到了什么？通过本节课的学习我们不但知道了著名的勾股定理，还通过

11、本节课的学习我们不但知道了著名的勾股定理，还知道从特殊到一般的探索方法及借助于图形的面积来探索、知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想验证数学结论的数形结合思想.、学了本节课后我们有什么感想？、学了本节课后我们有什么感想？ 很多的数学结论存在于平常的生活中，需要我们用数学很多的数学结论存在于平常的生活中，需要我们用数学的眼光去观察、思考、发现，这节课我们还受到了数学文化的眼光去观察、思考、发现，这节课我们还受到了数学文化辉煌历史的教育辉煌历史的教育.小结小结.勾股定理的运用勾股定理的运用已知直角三角形的任意两条边长，求第三已知直角三角形的任意两条边长，求

12、第三条边长条边长.a2=c2-b2b2=c2-a2c2=a2+b2.（三）随堂练习（三）随堂练习 1、在、在RtABC中，中， ，1）如果）如果a=3，b=4，则，则c=_；2）如果）如果a=6，b=8，则，则c=_；3）如果）如果a=5，b=12，则，则c=_；4) 如果如果a=15，b=20，则，则c=_.90C5101325. 2、下列说法正确的是（）、下列说法正确的是（）A.若若a、b、c是是ABC的三边，则的三边，则:B.若若a、b、c是是RtABC的三边，则的三边，则C.若若a、b、c是是RtABC的三边，的三边， ， 则则D.若若a、b、c是是RtABC的三边，的三边， ，则则2

13、22abc222abc90A222abc90C222abcD.3、一个直角三角形中，两直角边长分别为、一个直角三角形中，两直角边长分别为3和和4，下，下列说法正确的是（列说法正确的是（ ）A斜边长为斜边长为25 B三角形周长为三角形周长为25 C斜边长为斜边长为5 D三角形面积为三角形面积为204、如图、如图,三个正方形中三个正方形中,S125，S2144，则另一个，则另一个的面积的面积S3为为_ 5、一个直角三角形的两边长分别为、一个直角三角形的两边长分别为5cm和和12cm,则第则第三边的长为三边的长为 。第4题图S1S2S3C169.在直角三角形在直角三角形ABCABC中，中，C=90C

14、=900 0，A A、B B、C C所对的边分别为所对的边分别为a a、b b、c c （1 1） 已知已知a=1a=1，b=2b=2，求，求c c （2 2） 已知已知a=10a=10，c=15c=15，求，求b bACBbac.例例2：将长为：将长为5米的梯子米的梯子AC斜靠在墙上，斜靠在墙上，BC长为长为2米，求梯子上端米，求梯子上端A到墙的底端到墙的底端B的距离的距离.CAB解：在解：在RtABC中，中，ABC=90 BC=2 ，AC=5 AB2= AC - BC = 5-2 =21 AB= （米）米） (舍去负值）舍去负值）21.做一做：做一做： P62540026xP的面积的面积

15、=_X=_X=_24225BACAB=_AC=_BC=_251520.求下列图中表示边的未知数求下列图中表示边的未知数x x、y y、z z的值的值. .8181144144x xy yz z625625576576144144169169X=15Y=5Z=7.比比一一比比看看谁谁算算得得又又快快又又准！准！求下列直角三角形中未知边的长求下列直角三角形中未知边的长x x: :可用勾股定理建立方程可用勾股定理建立方程.勾股定理运用二勾股定理运用二: :8 8x x171716162020 x x12125 5x xX=15X=12X=13. 1 1、直角、直角 ABCABC的两直角边的两直角边a=5,b=12,c=_a=5,b=12,c=_ 2、直角直角 ABCABC的一条直角边的一条直角边a=10,a=10,斜边斜边 c=26 c=26，则，则b= b= ( ).( ).、已知：C90，a=6a=6， a：b3：4，求求b b和和c c.cab13b=8 c