棱柱棱锥问题

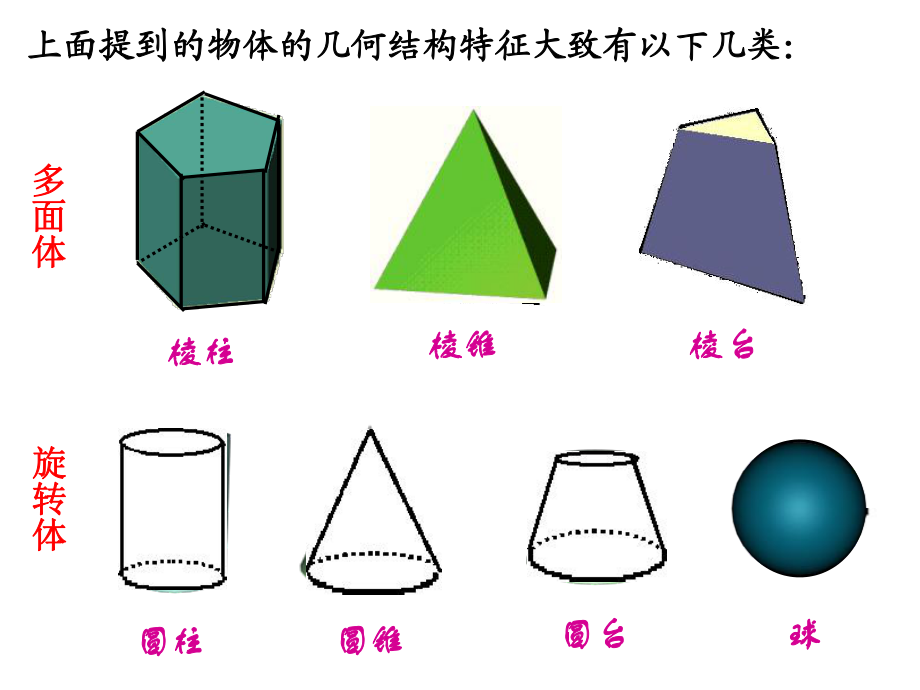
1、平行问题平行问题垂直问题垂直问题角度问题角度问题距离问题距离问题柱锥问题柱锥问题体积面积问题体积面积问题多面体与球的问题多面体与球的问题生活问题和翻折问题生活问题和翻折问题综合问题综合问题定义：由若干个平定义：由若干个平面多边形围成的几面多边形围成的几何体称为何体称为多面体多面体。定义：定义：由一个平面图形由一个平面图形绕它所在平面内的一条绕它所在平面内的一条定直线旋转形成的封闭定直线旋转形成的封闭几何体称为几何体称为旋转体旋转体。上面提到的物体的几何结构特征大致有以下几类：上面提到的物体的几何结构特征大致有以下几类：棱柱棱柱棱锥棱锥圆柱圆柱圆锥圆锥棱台棱台圆台圆台球球多面体多面体旋转体旋转体

2、棱柱棱柱 有两个面互相平行，其余各有两个面互相平行，其余各面都是面都是四边形四边形，并且每相邻两，并且每相邻两个面的公共边都平行，由这些个面的公共边都平行，由这些面所围成的几何体叫面所围成的几何体叫棱柱棱柱。侧棱侧棱底面底面顶点顶点侧侧面面（1 1）底面是全等的多边形）底面是全等的多边形DABCEFFAEDBC（2 2）侧面都是平行四边形）侧面都是平行四边形（3 3）侧棱平行且相等）侧棱平行且相等特点：特点：高高底面侧面棱DABCEFFAEDBC 思考：倾斜思考：倾斜后的几何体还是后的几何体还是棱柱吗？棱柱吗？复习：复习：知识网络知识网络棱柱棱柱(分类分类)棱棱柱柱斜棱柱斜棱柱直棱柱直棱柱正棱

3、柱正棱柱 棱柱的底面可以是三角形、四边形、五边形棱柱的底面可以是三角形、四边形、五边形我们我们把这样的棱柱分别叫做把这样的棱柱分别叫做三棱柱三棱柱、四棱柱四棱柱、五棱柱五棱柱1. 侧棱不垂直于底的棱柱叫做侧棱不垂直于底的棱柱叫做斜棱柱斜棱柱。2.侧棱垂直于底的棱柱叫做侧棱垂直于底的棱柱叫做直棱柱直棱柱。3. 底面是正多边形的直棱柱叫做底面是正多边形的直棱柱叫做正棱柱正棱柱。棱柱的表示法棱柱的表示法(下图下图)用平行的两底面多边形的字母表示棱柱用平行的两底面多边形的字母表示棱柱,如：如： 五棱柱五棱柱ABCDE- A1B1C1D1E1 。四棱柱四棱柱四棱柱四棱柱直四棱柱直四棱柱侧棱垂直底面侧棱垂

4、直底面平行六面体平行六面体底面是平行四边形底面是平行四边形长方体长方体正四棱柱正四棱柱正方体正方体侧面垂直侧面垂直底面底面l2=a2+b2+c2SABCD顶点顶点侧面侧面侧棱侧棱底面底面 有一个面是多边形，其余有一个面是多边形，其余各面都是有一个公共顶点的三各面都是有一个公共顶点的三角形所围成的几何体叫角形所围成的几何体叫棱锥棱锥棱锥棱锥（1 1）底面是多边形）底面是多边形（2 2）侧面都是三角形）侧面都是三角形（3 3）侧棱相交于一点）侧棱相交于一点高高O三棱锥三棱锥四棱锥四棱锥五五棱锥棱锥（四面体）（四面体） 如果一个棱锥的底面是正多边如果一个棱锥的底面是正多边形，并且顶点在底面的射影是底

5、形，并且顶点在底面的射影是底面的中心，这样的棱锥是面的中心，这样的棱锥是正棱锥正棱锥.OSABCDE 各侧棱相等，各侧面各侧棱相等，各侧面 是全等是全等的等腰三角形，各等腰的等腰三角形，各等腰 三角形底三角形底边上的高相等（它叫做正棱锥的边上的高相等（它叫做正棱锥的斜高斜高）。）。棱锥的表示方法：用表示顶点和底面的字母表示，棱锥的表示方法：用表示顶点和底面的字母表示，如五棱锥如五棱锥S-ABCDES-ABCDE。斜高斜高棱锥棱锥棱锥棱锥正四棱锥正四棱锥正三棱锥正三棱锥正四面体正四面体体积体积V VSh/3Sh/3顶点在底面正多边形的射影是底面的中心 用一个平行于棱锥底面用一个平行于棱锥底面的平

6、面去截棱锥，底面与截的平面去截棱锥，底面与截面之间的部分是面之间的部分是棱台棱台. .棱台棱台（1 1）底面是相似的多边形）底面是相似的多边形（2 2）侧面都是梯形）侧面都是梯形（3 3）侧棱延长线交于一点）侧棱延长线交于一点B B1 1A A1 1C C1 1D D1 1C C1 1 B B1 1A A1 1D D1 1上底面上底面下底面下底面侧面侧面顶点顶点侧棱侧棱底面侧面棱 由三棱锥、四棱锥、五棱锥由三棱锥、四棱锥、五棱锥截得的棱台，分别截得的棱台，分别叫做叫做三棱台三棱台，四棱台四棱台，五棱台五棱台棱台的表示法：棱台的表示法：棱台用表示上、下底面各顶点的字母来表示，棱台用表示上、下底面

7、各顶点的字母来表示，如下图，棱台如下图，棱台ABCD-ABCD-1 1B B1 1C C1 1D D1 1 。C C1 1 B B1 1A A1 1D D1 1斜高斜高用正棱锥截得的棱台叫作正棱台。用正棱锥截得的棱台叫作正棱台。正棱台的侧面是全等的等腰梯形，正棱台的侧面是全等的等腰梯形，它的高叫作正棱台的斜高。它的高叫作正棱台的斜高。正棱锥正棱锥正四棱台正四棱台AAOO 如何描述下图的几何结构特征？如何描述下图的几何结构特征？AAOO 以矩形的一边所在直线为以矩形的一边所在直线为旋转轴，其余边旋转形成的曲旋转轴，其余边旋转形成的曲面所围成的几何体叫做面所围成的几何体叫做圆柱圆柱圆柱圆柱旋转轴旋

8、转轴底面底面侧面侧面母线母线（1 1）底面是平行且半径相等的圆）底面是平行且半径相等的圆（2 2）侧面展开图是矩形）侧面展开图是矩形（3 3）母线平行且相等）母线平行且相等（4 4）平行于底面的截面是与）平行于底面的截面是与底面平行且半径相等的圆底面平行且半径相等的圆（5 5）轴截面是矩形）轴截面是矩形 以直角三角形的一条直角以直角三角形的一条直角边所在直线为旋转轴，其余边所在直线为旋转轴，其余两边旋转形成的曲面所围成两边旋转形成的曲面所围成的几何体叫做的几何体叫做圆锥圆锥圆锥圆锥（1 1）底面是圆）底面是圆（2 2）侧面展开图是以母线长为半径的扇形）侧面展开图是以母线长为半径的扇形（3 3）

9、母线相交于顶点）母线相交于顶点（4 4）平行于底面的截面是与底）平行于底面的截面是与底面平行且半径不相等的圆面平行且半径不相等的圆（5 5）轴截面是等腰三角形）轴截面是等腰三角形顶点顶点AB底面底面轴轴侧侧面面母母线线SO用表示它的轴的字母表示，如圆锥用表示它的轴的字母表示，如圆锥SOSO。 用一个平行于圆锥底用一个平行于圆锥底面的平面去截圆锥，底面面的平面去截圆锥，底面与截面之间的部分是与截面之间的部分是圆台圆台. .圆台圆台OO 圆柱、圆锥可以看圆柱、圆锥可以看作是由矩形或三角形绕作是由矩形或三角形绕其一边旋转而成，圆台其一边旋转而成，圆台是否也可看成是某图形是否也可看成是某图形绕轴旋转而

10、成？绕轴旋转而成？锥锥体体柱柱体体台台体体 棱柱、棱锥、棱台之间有什么关系？圆柱、圆锥、棱柱、棱锥、棱台之间有什么关系？圆柱、圆锥、圆台之间呢？柱、锥、台体之间有什么关系？圆台之间呢？柱、锥、台体之间有什么关系？上底扩大上底扩大上底缩小上底缩小上底缩小上底缩小上底扩大上底扩大球球 以半圆的直径所在的直线以半圆的直径所在的直线为旋转轴，将半圆旋转所形成为旋转轴，将半圆旋转所形成的曲面叫作的曲面叫作球面球面，球面所围成，球面所围成的几何体叫作的几何体叫作球体球体，简称，简称球球。球心球心半径半径直径直径O想一想：想一想：用一个平面去截一个球用一个平面去截一个球,截面是什么截面是什么?O 用一个截面

11、去截一用一个截面去截一个球，截面是圆面。个球，截面是圆面。球面被经过球心的平面截得的圆叫做球面被经过球心的平面截得的圆叫做。球面被不过球心的截面截得的圆叫球的球面被不过球心的截面截得的圆叫球的。球、圆柱、圆锥、圆台过轴的截面分别是什么图形？球、圆柱、圆锥、圆台过轴的截面分别是什么图形？柱体柱体锥体锥体台体台体球球多面体多面体旋转体旋转体 日常生活中我们常用到的日用品，比如：消毒液、日常生活中我们常用到的日用品，比如：消毒液、暖瓶、洗洁精等的主要几何结构特征是什么？暖瓶、洗洁精等的主要几何结构特征是什么？ 由柱、锥、台、球组成了一些简单的组合体认由柱、锥、台、球组成了一些简单的组合体认识它们的结

12、构特征要注意整体与部分的关系识它们的结构特征要注意整体与部分的关系圆柱圆柱圆台圆台圆柱圆柱ABCDEF例例用斜二测画法画水平放置的六边形的直观图用斜二测画法画水平放置的六边形的直观图(1)在六边形在六边形ABCDEF中，取中，取AD所在的直线为所在的直线为X轴，对称轴轴，对称轴MN所在直线为所在直线为Y轴，两轴交于点轴，两轴交于点O画对应的画对应的 轴，两轴相交轴，两轴相交于点于点 ，使，使,X YO45X OY MNOyxOxy注意：注意：(1)建系时要尽量考虑图形的对称性建系时要尽量考虑图形的对称性 (2)画水平放置平面图形的关键是画水平放置平面图形的关键是确定多边形顶点的位置确定多边形顶

13、点的位置OxyABCDEFMNABCDEFMNOyx，在，在 轴上取轴上取(2)以以O为中心，在为中心，在 上取上取xA DAD y12M NMN B CxN以点以点为中心，画为中心，画BC轴，并等于轴，并等于M，再以，再以为中心，画为中心，画E FxEF轴，并等于轴，并等于注意：注意：水平放置的线段长不变，铅垂放置的线段长变为原水平放置的线段长不变，铅垂放置的线段长变为原 来的一半来的一半OxyABCDEFMNABCDEFMNOyx 并擦去辅助线并擦去辅助线x轴和轴和y轴，便获得轴，便获得正六边形正六边形ABCDEF水平放置的直观图水平放置的直观图A B C D E F(3)连接连接,A B

14、 C D E F F A请您总结斜二测画法画水平放置的平面图形的方法步骤请您总结斜二测画法画水平放置的平面图形的方法步骤斜二测画法的步骤斜二测画法的步骤(1)在已知图形中取互相垂直的在已知图形中取互相垂直的x轴和轴和y轴，两轴相交于轴，两轴相交于O点点.画直观图时，把它画成对应的画直观图时，把它画成对应的x轴、轴、y轴，两轴交于轴，两轴交于O，使，使 ，它们确定的平面表示水平平面，它们确定的平面表示水平平面45 (135 )x Oy或或(2)已知图形中平行于已知图形中平行于x轴或轴或y轴的线段，在直观图中分别画轴的线段，在直观图中分别画成平行于成平行于x轴或轴或y轴的线段轴的线段(3)已知图形

15、中平行于已知图形中平行于x轴的线段，在直观图中保持原长度不轴的线段，在直观图中保持原长度不变；平行于变；平行于y轴的线段，长度为原来的一半轴的线段，长度为原来的一半例例2用用斜二测画法斜二测画法画长画长,宽宽,高分别是高分别是4cm,3cm,2cm的长方的长方体的直观图体的直观图 联想水平放置的平联想水平放置的平面图形的画法，并注意面图形的画法，并注意到高的处理到高的处理(2)MNPQ画画底底面面. .以以O O为为中中心心, ,在在x x轴轴上上取取线线段段M MN N, ,使使M MN N= = c cm m; ;在在轴轴上上取取线线段段P PQ Q, ,使使P PQ Q= = c cm

16、m; ;分分别别过过点点和和作作y y轴轴的的平平行行线线, ,过过点点和和作作x x轴轴的的平平行行线线, ,设设它它们们的的交交点点分分别别为为A A, ,B B, ,C C, ,D D, ,四四边边形形A AB BC CD D就就是是长长方方形形的的底底面面A AB BC CD DxyZOxyZOABCDMNPQ41.5 ,.xOz 190画画轴轴. .画画x x轴轴, ,y y轴轴, ,z z轴轴, ,三三轴轴交交于于点点O O, ,使使 x xO Oy y= =4 45 5xyZOABCD 3 3 画画侧侧棱棱. .过过A A, ,B B, ,C C, ,D D, ,各各点点分分别别

17、作作z z轴轴的的平平行行线线, ,并并在在这这些些平平行行线线上上分分别别截截取取2 2c cm m长长的的线线段段A AA A , ,B BB B , ,C CC C , ,D DD D . .MNPQ ,4 4 成成图图. .顺顺次次连连接接A A , ,B B , ,C C , ,D D , ,并并加加以以整整理理( (去去掉掉辅辅助助线线, ,将将被被遮遮挡挡住住的的部部分分改改为为虚虚线线) )就就可可得得到到长长方方体体的的直直观观图图. .ABCDACDBABCD例例3 3已知几何体的三视图，用斜二测画法画出它的直观图已知几何体的三视图，用斜二测画法画出它的直观图xyOOxyZ

18、OOOO正视图正视图侧视图侧视图俯视图俯视图HPCBDAO棱锥基本性质棱锥基本性质如果棱锥被平行于底如果棱锥被平行于底面的平面所截，那么面的平面所截，那么截面和底面截面和底面相似相似，并，并且它们且它们面积的比面积的比等于等于截得的棱锥的高与已截得的棱锥的高与已知棱锥的高的知棱锥的高的平方比平方比CBDADCBADCBASS2222PHPO 棱锥基本性质棱锥基本性质棱锥的高、斜高和斜棱锥的高、斜高和斜高在底面的射影组成高在底面的射影组成一个直角三角形。棱一个直角三角形。棱锥的高、侧棱和侧棱锥的高、侧棱和侧棱在底面的射影组成一在底面的射影组成一个直角三角形个直角三角形PCBDAHERt PEHR

19、t PHBRt PEBRt BEH正棱锥正棱锥如果一个棱锥如果一个棱锥 的的底面是正多底面是正多边形边形，并且并且顶顶点在底面的射点在底面的射影是底面中心影是底面中心这样的棱锥叫这样的棱锥叫做正棱锥做正棱锥1 1、侧面与底面所成的角、侧面与底面所成的角都相等的棱锥是正棱锥都相等的棱锥是正棱锥2 2、棱锥的高可以等于它、棱锥的高可以等于它的一条侧棱长的一条侧棱长3 3、棱锥的高一定在棱锥、棱锥的高一定在棱锥的内部的内部4 4、侧面均为全等的等腰、侧面均为全等的等腰三角形的棱锥是正棱锥三角形的棱锥是正棱锥判断正误判断正误在下列条件下，判断正三棱锥在下列条件下，判断正三棱锥P-ABC的顶点的顶点P在

20、底面在底面ABC内的射影位置内的射影位置1 1、三条侧棱相等、三条侧棱相等2 2、侧棱与底面所成的角相等、侧棱与底面所成的角相等3 3、侧面与底面所成的角相等、侧面与底面所成的角相等4 4、顶点、顶点P P到到ABCABC的三边距离相等的三边距离相等5 5、三条侧棱两两垂直、三条侧棱两两垂直6 6、相对棱互相垂直、相对棱互相垂直7 7、三个侧面两两垂直、三个侧面两两垂直外心外心外心外心内心内心内心内心垂心垂心垂心垂心垂心垂心有没有侧棱长和底面边长相等的正四棱锥？有没有侧棱长和底面边长相等的正四棱锥？有没有侧棱长和底面边长相等的正五棱锥？有没有侧棱长和底面边长相等的正五棱锥？有没有侧棱长和底面边

21、长相等的正六棱锥？有没有侧棱长和底面边长相等的正六棱锥？1.一个三棱锥，如果它的底面是直角三角形，一个三棱锥，如果它的底面是直角三角形，那么它的三个侧面那么它的三个侧面( )(A)至多只有一个是直角三角形至多只有一个是直角三角形(B)至多只有两个是直角三角形至多只有两个是直角三角形(C)可能都是直角三角形可能都是直角三角形(D)必然都是非直角三角形必然都是非直角三角形C2.命题：命题：底面是正多边形的棱锥，一定是正棱锥；底面是正多边形的棱锥，一定是正棱锥；所有的侧棱的长都相等的棱锥，一定是正棱锥；所有的侧棱的长都相等的棱锥，一定是正棱锥；各侧面和底面所成的二面角都相等的棱锥，一定是正棱各侧面和

22、底面所成的二面角都相等的棱锥，一定是正棱锥；锥；底面多边形内接于一个圆的棱锥，它的侧棱长都相等；底面多边形内接于一个圆的棱锥，它的侧棱长都相等；一个棱锥可以有两条侧棱和底面垂直；一个棱锥可以有两条侧棱和底面垂直；一个棱锥可以有两个侧面和底面垂直一个棱锥可以有两个侧面和底面垂直.其中正确的有其中正确的有 ( )(A)0个个 (B)1个个 (C)3个个 (D)5个个C2.正三棱柱正三棱柱ABC-A1B1C1中，若中，若AB=2 BB1，则，则AB1与与C1B所成角的大小是所成角的大小是 （ ）A.60o B.90o C.105o D.75oB3.长方体三边之和为长方体三边之和为a+b+c=6，总面

23、积为，总面积为11，则，则其对角线长为其对角线长为_；若一条对角线与二个面所成的；若一条对角线与二个面所成的角为角为30或或45，则与另一个面所成的角为，则与另一个面所成的角为_；若一条对角线与各条棱所成的角为；若一条对角线与各条棱所成的角为、，则，则sin、sin、sin的关系为的关系为_.sin2+sin2+sin2=2530HOCBDAPCBDA设棱锥的底面积是设棱锥的底面积是8cm8cm2 2, ,则这个棱锥则这个棱锥的中截面（过棱锥的高的中点且平的中截面（过棱锥的高的中点且平行于底面的截面）的面积是多少？行于底面的截面）的面积是多少？DCBADCBASS22PHPO 8DCBAS41

24、 S中中=2过棱锥的高的三等分点作两个平行过棱锥的高的三等分点作两个平行于底面的截面于底面的截面, ,它将棱锥的侧面分为它将棱锥的侧面分为三部分面积之比三部分面积之比( (自上而下自上而下) )为为 。过棱锥的高作两个平行于底面的截面，过棱锥的高作两个平行于底面的截面，它将棱锥的侧面分为三部分面积相等则它将棱锥的侧面分为三部分面积相等则它分棱锥的高的比是它分棱锥的高的比是( (自上而下）自上而下） 。正三棱锥的底面边长为正三棱锥的底面边长为a.a.侧棱长为侧棱长为b,b,求它的高和侧面积？求它的高和侧面积？PABCDO正三棱锥的底面边长为正三棱锥的底面边长为1.1.侧面与底侧面与底面所成的角为

25、面所成的角为60,60,求它的高和相邻两求它的高和相邻两侧面所成的二面角的大小？侧面所成的二面角的大小？PABCDOE正正四四棱锥的底面边长为棱锥的底面边长为1.1.侧面与底侧面与底面所成的角为面所成的角为60,60,求它的高和相邻两求它的高和相邻两侧面所成的二面角的大小？侧面所成的二面角的大小？PABDCOEF正三棱锥的底面边长为正三棱锥的底面边长为a .a .侧棱与底面所侧棱与底面所成的角为成的角为60,60,过底面一边做一截面使其与过底面一边做一截面使其与底面成底面成3030的二面角，求此截面面积？的二面角，求此截面面积？PABCOEF 已知已知: :三棱锥三棱锥P-ABCP-ABC的底

26、面是等腰三角的底面是等腰三角形形,AB=AC=10,BC=12,AB=AC=10,BC=12,棱锥的侧面与底面棱锥的侧面与底面所成的二面角都是所成的二面角都是45,45,求棱锥的侧面积求棱锥的侧面积? ?DPABCO连接棱长都是连接棱长都是a a的正三棱锥的侧面中心的正三棱锥的侧面中心成一个三角形，求此三角形的面积？成一个三角形，求此三角形的面积？PABC在正四棱锥内有一个内接正方体，这正方在正四棱锥内有一个内接正方体，这正方体的四个顶点在四棱锥的侧棱上，另四个体的四个顶点在四棱锥的侧棱上，另四个顶点在棱锥底面上，若棱锥底面边长为顶点在棱锥底面上，若棱锥底面边长为a,a,高为高为h h，求内接

27、正方体的棱长？，求内接正方体的棱长？ABDCOPHEF设内接正方体的棱长为设内接正方体的棱长为x xOCEHPOPH axhxh2222 haahx 在正三棱锥在正三棱锥P-ABCP-ABC的底面边长和高都是的底面边长和高都是4 4，其内接正三棱柱的三个侧面都是正，其内接正三棱柱的三个侧面都是正方形，求内接正三棱柱的全面积？方形，求内接正三棱柱的全面积？PABC4. 在底面是直角梯形的四棱锥在底面是直角梯形的四棱锥P-ABCD中，中，侧棱侧棱PA底面底面ABCD，ABC=90，PA=AB=BC=2，AD=1, (1)求求D到平面到平面PBC的距离；的距离； (2)求面求面PAB与面与面PCD所

28、成的二面角的大小。所成的二面角的大小。APDCB解解: (1)AD/平面平面PBCD到平面到平面PBC的距离等于的距离等于A到到平面平面PBC的距离的距离PABC, ABBCBC平面平面PAB平面平面PBC平面平面PABA到到PB的距离就是的距离就是A到平面到平面PBC的距离的距离PA=AB=2, PAAB,A到到PB的距离为的距离为2222222 D到平面到平面PBC的距离为的距离为24. 在底面是直角梯形的四棱锥在底面是直角梯形的四棱锥P-ABCD中，中，侧棱侧棱PA底面底面ABCD，ABC=90，PA=AB=BC=2，AD=1, (1)求求D到平面到平面PBC的距离；的距离； (2)求面

29、求面PAB与面与面PCD所成的二面角的大小。所成的二面角的大小。APDCBQ (2)延长延长CD与与BA相交于相交于Q,ADBC,且且 AD= BC21A是是QB的中点的中点,又又PA=AB=AQBQPQ,又又BC平面平面PAB,CPPQ,故故CPB是所求二面角的是所求二面角的平面角平面角,22tan BPBCCPB故面故面PCD与面与面PCD所成的二面角为所成的二面角为22arctan例题讲解例题讲解1 1、四棱锥、四棱锥P-ABCDP-ABCD的底面是边长为的底面是边长为a a的正方形，的正方形，PBPB面面ABCD.ABCD.(1)(1)若面若面PADPAD与面与面ABCDABCD的二面

30、角为的二面角为60600 0，求四棱锥的体积；，求四棱锥的体积；作、作、 证、证、 求？求？APDCB PB PB面面ABCDABCD，BAADBAAD，PAADPAADPABPAB就是面就是面PADPAD与面与面ABCDABCD的二面角的平面角的二面角的平面角解：解：即即PABPAB60600 0在在RtPABRtPAB中，中，ABABa a， PABPAB60600 0PBPBa a3V= aV= a3 333例题讲解例题讲解1 1、四棱锥、四棱锥P-ABCDP-ABCD的底面是边长为的底面是边长为a a的正方形，的正方形，PBPB面面ABCD.ABCD.(2)(2)证明不论高证明不论高P

31、BPB怎样变化，面怎样变化，面PADPAD与面与面PCDPCD所成的二面角恒大于所成的二面角恒大于90900 0. .APDCBM证：由题设侧面证：由题设侧面PADPAD与与PCDPCD为全等为全等，作作CMPDCMPD于于M M，连结，连结MAMA，则，则CDMADMCDMADM，AMAMCMCM，AMDAMD90900 0故故AMCAMC就是所证二面角的平面角就是所证二面角的平面角. .连结连结ACAC在在AMCAMC中，由余弦定理中，由余弦定理cosAMC =cosAMC =MCAMACMC 2AM22202222 MCAMACCDAD故故AMCAMC90900 0，即证，即证. .小结

32、小结：作二面角平面角的方法作二面角平面角的方法有面的垂线，则一作一连法有面的垂线，则一作一连法定义法，在两面内作棱的垂线定义法，在两面内作棱的垂线面积射影定理面积射影定理变化一变化一 四棱锥四棱锥P-ABCDP-ABCD的底面是边长为的底面是边长为a a的的菱形菱形，BCDBCD60600 0，PBPB面面ABCD.ABCD.若面若面PADPAD与面与面ABCDABCD的二面角为的二面角为60600 0，求四棱锥的体积；求四棱锥的体积；APDCBE四棱锥四棱锥P-ABCDP-ABCD的底面是边长为的底面是边长为a a的的菱形菱形，BCDBCD60600 0，面面PBCPBC面面ABCDABCD

33、，且，且PBCPBC是等边是等边. . 求侧面求侧面PADPAD与底面与底面ABCDABCD所成的二面角；所成的二面角；APDCB变化二变化二E注意注意：面面垂直的应用面面垂直的应用分析平面图形分析平面图形例题讲解例题讲解2 2、如图在直三棱柱、如图在直三棱柱ABC-AABC-A1 1B B1 1C C1 1中，底面中，底面ABCABC是等腰是等腰RtRt， C=90 C=900 0 ，D D、E E分别分别是是CCCC1 1和和A A1 1B B的中点，的中点，AC=AAAC=AA1 1=2=2 (1) (1)求线段求线段DEDE的长的长B B1 1B BA AD DA A1 1E EC C

34、C C1 1F解：取解：取ABAB的中点的中点F F，连结，连结EFEF，CFCF，EF/AAEF/AA1 1/CC1/CC1DD是中点，是中点，EF CDEF CD/DE=CFDE=CF在在ABCABC中，中，CFCF2DEDE2例题讲解例题讲解2 2、如图在直三棱柱、如图在直三棱柱ABC-AABC-A1 1B B1 1C C1 1中，底面中，底面ABCABC是等腰是等腰RtRt， C=90 C=900 0 ，D D、E E分别分别是是CCCC1 1和和A A1 1B B的中点，的中点，AC=AAAC=AA1 1=2=2(2)(2)求二面角求二面角A-BD-CA-BD-C的大小的大小( (反

35、三角表示反三角表示) )MB B1 1B BA AD DA A1 1E EC CC C1 1解：解： ABC-A ABC-A1 1B B1 1C C1 1是直棱柱，是直棱柱，ACBCACBC，ACAC侧面侧面BBBB1 1C C1 1C C，作作CMBDCMBD于于M M，连结，连结AMAM，则则AMCAMC就是所求二面角的平面角；就是所求二面角的平面角；在在ACMACM中，中，ACAC2 2CMCM552tanAMC=AC/CM=tanAMC=AC/CM=5即所求为即所求为5arctanACCMACCM，例题讲解例题讲解3 3、如图在直三棱柱、如图在直三棱柱ABC-AABC-A1 1B B1 1C C1 1中，底面中，底面ABCABC是等腰是等腰RtRt，C=90C=900 0 ，D D、E E分别是分别是CCCC1 1和和A A1 1B B的中点，的中点，AAAA1 12 2，若点，若点E E在平面在平面ABDABD上的射影是上的射影是ABDABD的重心的重心G.G. (1) (1)求求A A1 1B B与平面与平面ABDABD所成的角所成的角( (用反三角表示用反三角表示) )；B B1 1B BA AD DA A1 1E EC CC C1 1GFM解：连结解：连结BGBG，