《高等数学》电子（同济第六版）04第三章 第4节 函数单调性与曲线的凹凸性ppt课件

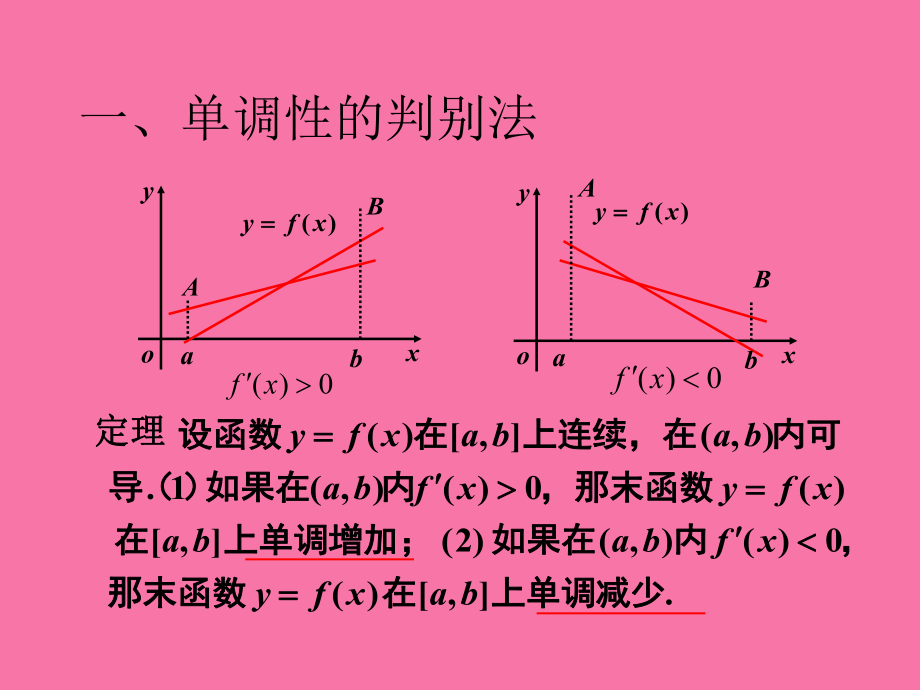
1、拐点函数的单调性与曲线的第四节一、单调性的判别法点二、曲线的凹凸性及拐三、小结及作业一、单调性的判别法xyo)(xfy xyo)(xfy abAB( )0fx( )0fx定理定理.,)(0)(),()2(,)(0)(),(1.),(,)(上上单单调调减减少少在在那那末末函函数数，内内如如果果在在上上单单调调增增加加；在在，那那末末函函数数内内如如果果在在）（导导内内可可上上连连续续，在在在在设设函函数数baxfyxfbabaxfyxfbababaxfy abBA证证12, , ,x xa b,21xx 且且运用拉氏定理运用拉氏定理,得得)()()()(211212xxxxfxfxf , 012

2、 xx, 0)(),( xfba内，内，若在若在, 0)( f则则).()(12xfxf .,)(上上单单调调增增加加在在baxfy , 0)(),( xfba内，内，若在若在, 0)( f则则).()(12xfxf .,)(上单调减少上单调减少在在baxfy 上上的的单单调调性性。在在讨讨论论例例2 , 0sin1 xxy解：解：),2 , 0(, 0cos1 xxy上单调增加。上单调增加。在在2 , 0sin xxy说明：说明：1 , a b（）把换成无穷区间定理仍成立082)()2,(82)(2xxfxxxf上上在在如如( )(, 2f x 在上单调增加。例例2 2解解.1的单调性的单调

3、性讨论函数讨论函数 xeyx. 1 xey,)0 ,(内内在在 , 0 y函数单调减少；函数单调减少；,), 0(内内在在, 0 y.函函数数单单调调增增加加留意留意: :函数的单调性是一个区间上的性质，要用函数的单调性是一个区间上的性质，要用导数在这一区间上的符号来断定，而不能用一导数在这一区间上的符号来断定，而不能用一点处的导数符号来判别一个区间上的单调性点处的导数符号来判别一个区间上的单调性).,(: D又又2函数在整个定义域上不一定是单调的，但在不函数在整个定义域上不一定是单调的，但在不同的区间上具有单调性，且改动单调性的点只能够同的区间上具有单调性，且改动单调性的点只能够是的是的 点

4、及导数不存在的点点及导数不存在的点0)( xf上上不不单单调调在在如如2 , 0sin xy 2 23 2上上单单调调但但在在2 ,23,23,2,2, 0 0)23()2( ff且且。点不可导但改变单调性点不可导但改变单调性在在再如再如0 xxy4区间内个别点导数为零区间内个别点导数为零,不影响区间的单调性不影响区间的单调性.例如例如,3xy , 00 xy.),(上单调增加上单调增加但在但在x3xy 3讨论函数单调性的步骤：讨论函数单调性的步骤：1确定函数的定义域；确定函数的定义域；2求函数导数为零的点及一阶导数不存在的点；求函数导数为零的点及一阶导数不存在的点；3这些点将定义域分成假设干

5、个小区间，列表讨论。这些点将定义域分成假设干个小区间，列表讨论。31292)(23xxxxf的单调区间的单调区间.解解:12186)(2xxxf)2)(1(6xx令,0)( xf得2, 1xxx)(xf )(xf) 1,(2001)2,1 (),2(21故)(xf的单调增区间为(,1,2,) )(xf的单调减区间为1, 2 函数的定义域为（- ，）且任点都可导；例例3 确定函数确定函数例例4 4解解.)(32的单调区间的单调区间确定函数确定函数xxf ).,(: D)0(,32)(3 xxxf.,0导数不存在导数不存在时时当当 x时时，当当0 x, 0)( xf上单调增加；上单调增加；在在),

6、 0 时，时，当当 x0, 0)( xf上单调减少；上单调减少；在在0 ,(单调区间为单调区间为，0 ,()., 0 32xy 例例5 5证证0,ln(1).xxx当时 试证成立),1ln()(xxxf 设设.1)(xxxf 则则, 0)(), 0(,), 0)( xfxf可可导导，且且上上连连续续在在上单调增加；上单调增加；在在), 0 , 0)0( f时，时，当当0 x, 0)1ln( xx).1ln(xx 即即(5) 利用单调性可证明不等式。00 )()(fxf6例例时，时，当当20 x。证证明明21sin2xxex证明： )21 (sin)(2xxexfx作作20 xxxexffxco

7、s)(0)0(0cos)(0)0( xexffx因此， 单调减少, 0)0()( fxf单单调调减减少少，)(xf 0)0()(fxff(x) 单调减少 0)0()( fxf也就是 0)21 (sin2xxex21sin2xxex)(xf 1sin)(0)0( xexffx7例例只只有有一一个个实实根根。证证明明0123xxx证明：证明：1)(23xxxxf令令123)(2xxxf032)31( 32x上严格单增上严格单增在在),()(xf根根。所所以以方方程程最最多多有有一一个个实实, 01)0(f又又051248)2(f上至少有一实根，上至少有一实根，在在所以所以0 , 2)(xf即方程只

8、有一个实根即方程只有一个实根问题问题:如何研讨曲线的弯曲方向如何研讨曲线的弯曲方向?xyoxyo1x2x)(xfy 图形上恣意弧段位图形上恣意弧段位于所张弦的上方于所张弦的上方xyo)(xfy 1x2x图形上恣意弧段位图形上恣意弧段位于所张弦的下方于所张弦的下方ABC点二、曲线的凹凸性及拐1. 曲线的凹凸与拐点的定义定义定义 1. 1. 设函数设函数)(xf 在区间 上延续 , ,21Ixx(1) 假设恒有,2)()()2(2121xfxfxxf那么称 的图形)(xf是凹的;(2) 假设恒有,2)()()2(2121xfxfxxf那么称 的图形)( xf函数图形上凹凸的分界点称为拐点 .是凸的

9、 .yox2x1x221xx yox1x221xx 2xyoxI2、曲线凹凸的断定xyo)(xfy xyo)(xfy abAB递增递增)(xf abBA0 y递递减减)(xf 0 y定理定理1 1.,)(, 0)()2(;,)(, 0)()1(),(,),(,)(上上的的图图形形是是凸凸的的在在则则上上的的图图形形是是凹凹的的在在则则内内若若在在二二阶阶导导数数内内具具有有在在上上连连续续在在如如果果baxfxfbaxfxfbababaxf 证证: :,21baxx利用一阶泰勒公式可得)()(1fxf221xx !2)(1f 21)(x221xx )()(2fxf221xx )(f 221xx

10、 )(2x221xx !2)(2f 22)(x221xx 两式相加两式相加)(2)()(21fxfxf221xx 22!21)(12xx )()(21ff ),(2)()(21fxfxf221xx ),(2)()(21fxfxf221xx )(f 221xx )(1x221xx 21121212122222)()()()()(xxxfxxxxxfxxfxf 时时，当当0)( xf）式成立。）式成立。（1）式成立。）式成立。（2时时，当当0)( xf例例1.1.判别曲线判别曲线4xy 的凹凸性.解解: :,43xy 212xy 当0 x时, 0 y0 x时0 y故曲线4xy 在),(上是向上凹的

11、.x阐明阐明 (1) 在个别二阶导数为 0 的点, 假设此点两侧二阶导数不变号, 那么不改动曲线的凹凸性 .到到。最最大大（小小）值值在在边边界界达达为为凹凹（凸凸）函函数数，则则）如如果果函函数数在在闭闭区区间间上上（2例例2 2.3的的凹凹凸凸性性判判断断曲曲线线xy 解解,32xy ,6xy 时，时，当当0 x, 0 y为凸的；为凸的；在在曲线曲线0 ,(时，时，当当0 x, 0 y为凹的；为凹的；在在曲线曲线), 0 .)0 , 0(是曲线的拐点是曲线的拐点点点留意到留意到,例例3.3.求曲线求曲线3xy 的拐点. 解解: :,3231xy3592 xyxy y0)0,(),0(不存在

12、0因此点 ( 0 , 0 ) 为曲线3xy 的拐点 .不存在的点。不存在的点。导导能是二阶导为零及二阶能是二阶导为零及二阶）改变凹凸性的点只可）改变凹凸性的点只可（2c检查在这些点左右两边的符号，从而决议曲线 的凹凸区间及拐点。 )(xf 0)( xf)(xf 3判别曲线的凹凸性及拐点的方法步骤：判别曲线的凹凸性及拐点的方法步骤：a求出求出 ；b求出使求出使 的点及的点及 不存在的点；不存在的点；例例4.4.求曲线求曲线14334xxy的凹凸区间及拐点.解解:1) 求y ,121223xxyxxy24362 )(3632xx2) 求函数二阶导为零的点令0 y得,03221xx对应3) 列表判别

13、271121,1yy)0,(),0(3232),(y xy0320012711,点 ( 0 , 1 ) 及),(271132均为拐点.32) 1 , 0(),(271132故该曲线在),32(),0 ,(,上凹上凹)32, 0(上凸5例例20sin.2xxx证明：当时，有证明： xxxF 2sin)(作作0)2(,0)0( FF则则0sin)(,2cos)( xxFxxF 因因为为是是凸凸函函数数，所所以以)(xFy 0)2(),0(min)( FFxF202sin xxx从而从而6例 证明不等式)0, 0(2ln)(lnlnyxyxyxyyxx证明：证明：)0(ln)(zzzzf令令1ln)

14、(zzf)0(01)( zzzf是凹函数，是凹函数，)(zf)()(21)2(yfxfyxf2ln2)lnln(21yxyxyyxx即即2ln)(lnlnyxyxyyxx故故有有三、小结 单调性的判别是拉格朗日中值定理定单调性的判别是拉格朗日中值定理定理的重要运用理的重要运用. 定理中的区间换成其它有限或无限区定理中的区间换成其它有限或无限区间，结论依然成立间，结论依然成立. 运用：利用函数的单调性可以确定某运用：利用函数的单调性可以确定某些方程实根的个数和证明不等式些方程实根的个数和证明不等式.曲线的弯曲方向曲线的弯曲方向凹凸性凹凸性;凹凸性的断定凹凸性的断定.改动弯曲方向的点改动弯曲方向的

15、点拐点拐点;拐点的求法拐点的求法1, 2.15243P习题1,3(1,4,5,6),5(1,2,4,5),6,8(1,3),9(1,3,6),10(1,2),13,14思索题思索题设设)(xf在在),(ba内二阶可导，且内二阶可导，且0)(0 xf，其中其中),(0bax ，则，则,(0 x)(0 xf是否一定为是否一定为曲线曲线)(xf的拐点？举例说明的拐点？举例说明.思索题解答思索题解答因为因为0)(0 xf只是只是,(0 x)(0 xf为拐点为拐点的的必要条件必要条件，故故,(0 x)(0 xf不不一一定定是是拐拐点点.例例4)(xxf ),( x0)0( f但但)0 , 0(并并不不是

16、是曲曲线线)(xf的的拐拐点点.一、一、 填空题：填空题：1 1、 若函数若函数)(xfy 在在 （ba,） 可导， 则曲线） 可导， 则曲线)(xf在在( (ba,) )内取凹的充要条件是内取凹的充要条件是_._.2 2、 曲线上曲线上_的点，称作曲线的拐点的点，称作曲线的拐点 . .3 3、 曲线曲线)1ln(2xy 的拐点为的拐点为_._.4 4、 曲线曲线)1ln(xy 拐点为拐点为_._.二、二、 求曲线求曲线xeyarctan 的拐点及凹凸区间的拐点及凹凸区间 . .三、三、 利用函数图形的凹凸性，证明不等式：利用函数图形的凹凸性，证明不等式： 22yxyxeee )(yx . .

17、四、求曲线四、求曲线 2sin2cot2ayax的拐点的拐点 . .练练 习习 题题五、五、 试证明曲线试证明曲线112 xxy有三个拐点位于同一直线有三个拐点位于同一直线上上 . .六、六、 问问a及及b为何值时，点为何值时，点(1,3)(1,3)为曲线为曲线23bxaxy 的拐点？的拐点？七、七、 试决定试决定22)3( xky中中k的值的值, ,使曲线的拐点处使曲线的拐点处的法线通过原点的法线通过原点 . .一、一、1 1、),()(baxf在在 内递增或内递增或0)(),( xfbax； 2 2、凹凸部分的分界点；、凹凸部分的分界点；3 3、2 ,(), 2),2, 2(2e； 4 4

18、、)2ln, 1(),2ln, 1( . .二、拐点二、拐点),21(21arctane, ,在在21,( 内是凹的内是凹的, ,在在),21 内是凸的内是凸的. .四、拐点四、拐点)23,332(aa及及)23,332(aa . .五、五、).)32(431, 32(),)32(431, 32(),1, 1( 练习题答案练习题答案六六、29,23 ba. .七七、 82 k. .思索题思索题 若若0)0( f，是是否否能能断断定定)(xf在在原原点点的的充充分分小小的的邻邻域域内内单单调调递递增增？思索题解答思索题解答不能断定不能断定.例例 0, 00,1sin2)(2xxxxxxf )0(

19、f)1sin21(lim0 xxx 01 但但0,1cos21sin41)( xxxxxf )212(1kx当当 时，时，0)212(41)( kxf kx21当当 时，时，01)( xf留意留意 可以恣意大，故在可以恣意大，故在 点的任何邻点的任何邻域内，域内， 都不单调递增都不单调递增k00 x)(xf一一、 填填空空题题：1 1、 函函数数7186223 xxxy单单调调区区间间为为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _. .2 2、 函函数数212xxy 在在区区间间 - -1 1, ,1 1 上上单单调调_ _ _ _ _ _ _ _ _， 在在_ _ _ _ _ _ _ _ _ _上上单单调调减减. .3 3、函函数数22ln xxy 的的单单调调区区间间为为_ _ _ _ _ _ _ _ _ _ _ _ _， 单单减减区区间间为为_ _ _ _ _ _ _ _ _ _ _ _ _ _. .二二、 确确定定下下列列函函数数的的单单调调区区间间：1 1、 xxxy6941023 ；2 2、 32)(2(xaaxy ( (0 a) )；3 3、 xxy2sin . .练练 习习 题题三、三、 证明下列不等式：证明下