-力矩的时间累积效应

1、3-2力矩对时间的累积效应力矩对时间的累积效应 直线运动的描述（线量）：直线运动的描述（线量）： 位移、速度、加速度、力、动量、冲量、位移、速度、加速度、力、动量、冲量、动量定理动量定理 定轴转动运动的描述（角量）：定轴转动运动的描述（角量）： 角位移、角速度、角加速度、角力（力角位移、角速度、角加速度、角力（力矩）、角动量、角冲量（冲量矩）矩）、角动量、角冲量（冲量矩） 、角动、角动量定理量定理 13-2力矩对时间的累积效应力矩对时间的累积效应ipjp0, 0p一一 质点的角动量定理和角动量守恒定律质点的角动量定理和角动量守恒定律 22kvvmEmp，质点质点运动描述运动描述22kIEIL，

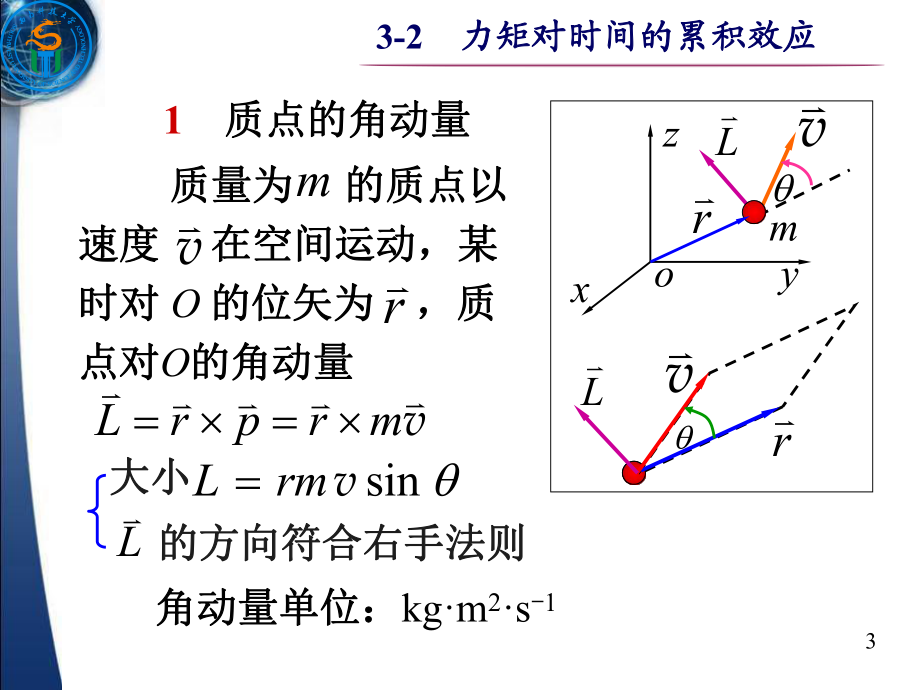
2、刚体刚体定轴转动描述定轴转动描述0, 0p23-2力矩对时间的累积效应力矩对时间的累积效应v1质点的角动量质点的角动量vmrprLvrLLrxyzom 质量为质量为 的质点以的质点以速度速度 在空间运动，某在空间运动，某时对时对 O 的位矢为的位矢为 ，质，质点对点对O的角动量的角动量mrvsinvrmL 大小大小 的方向符合右手法则的方向符合右手法则L角动量单位：角动量单位：kgm2s-133-2力矩对时间的累积效应力矩对时间的累积效应Lrpmo 质点以质点以 作半径为作半径为 的圆周运动，相对圆心的圆周运动，相对圆心rImrrmvL2tLMdd 作用于质点的合外力对作用于质点的合外力对参考

3、点参考点 O 的力的力矩，等于质点对该点矩，等于质点对该点 O 的的角动量角动量随时间的随时间的变化率变化率.2 质点的角动量定理质点的角动量定理43-2力矩对时间的累积效应力矩对时间的累积效应？，tLFtpddddptrtprprttLdddd)(ddddtLMddFrtprtLdddd0,ddptrvv质点角动量定理的推导质点角动量定理的推导prL53-2力矩对时间的累积效应力矩对时间的累积效应 质点的角动量定理：质点的角动量定理：对同一参考点对同一参考点O，质点所受的冲量矩等于质点角动量的增量质点所受的冲量矩等于质点角动量的增量.tLMddLM,0 恒矢量恒矢量 3 质点的角动量守恒定律

4、质点的角动量守恒定律12d21LLtMtt冲量矩冲量矩tMttd2163-2力矩对时间的累积效应力矩对时间的累积效应开普勒第二定律开普勒第二定律73-2力矩对时间的累积效应力矩对时间的累积效应 将行星看为质点将行星看为质点, ,dt 时间内以速度时间内以速度 完成的位完成的位移为移为 , ,矢径矢径 在在d t 时间内扫过的面积为时间内扫过的面积为dS。 vtv drtdvrSd21掠面速度掠面速度 讨论讨论：行星行星的掠面速度与角动量的掠面速度与角动量vrdtds21为一不变量为一不变量prL即为一不变量即为一不变量dtvfrrom83-2力矩对时间的累积效应力矩对时间的累积效应 例例1 一

5、半径为一半径为 R 的光滑圆环置于竖直平的光滑圆环置于竖直平面内面内. 一质量为一质量为 m 的小的小球穿在圆环上球穿在圆环上, 并可在并可在圆环上滑动圆环上滑动. 小球开始小球开始时静止于圆环上的点时静止于圆环上的点 A (该点在通过环心该点在通过环心 O 的的水平面上水平面上)，然后从，然后从 A点开始下滑设小球与圆环间的摩擦力略点开始下滑设小球与圆环间的摩擦力略去不计求小球滑到点去不计求小球滑到点 B 时对环心时对环心 O 的角的角动量和角速度动量和角速度93-2力矩对时间的累积效应力矩对时间的累积效应 解解 小球受力小球受力 、 作用作用, 的力矩为的力矩为零，重力矩垂直纸面向里零，重

6、力矩垂直纸面向里由质点的角动量定理由质点的角动量定理cosmgRM tLmgRddcostmgRLdcosdNFPNFtLMdd得：得：103-2力矩对时间的累积效应力矩对时间的累积效应考虑到考虑到tmRLdd,2dmgRmRcosd2得得21)sin2(RgtmgRLdcosddgRcosd00cosddgR2123)sin2(gmRL 113-2力矩对时间的累积效应力矩对时间的累积效应二二 刚体定轴转动的角动量定理刚体定轴转动的角动量定理 和角动量守恒定律和角动量守恒定律 1刚体定轴转动刚体定轴转动的角动量的角动量2iiirmLOirimivILziiirm)(2123-2力矩对时间的累积

7、效应力矩对时间的累积效应对定轴转的刚体对定轴转的刚体 ，exiMM2 刚体定轴转动的角动量定理刚体定轴转动的角动量定理质点质点mi受合力矩受合力矩Mi( (包括包括Miex、 Miin ) )()(2ddddddiiiiirmttItLM 0iniMtLtIMdddd)(tIrmtiidddd2)()(合外力矩合外力矩133-2力矩对时间的累积效应力矩对时间的累积效应非刚体非刚体定轴转动的角动量定理定轴转动的角动量定理112221dIItMtt1221dIItMtt3 刚体定轴转动的刚体定轴转动的角动量守恒定律角动量守恒定律0M IL，则，则若若=常量常量 对定轴转的刚体，受合外力矩对定轴转的

8、刚体，受合外力矩M，从从 到到 内，角速度从内，角速度从 变为变为 ，积分可得：，积分可得：212t1t143-2力矩对时间的累积效应力矩对时间的累积效应 角动量守恒定律是自然界的一个基本定律角动量守恒定律是自然界的一个基本定律. 内力矩不改变系统的角动量内力矩不改变系统的角动量. 守恒条件守恒条件0M若若 不变，不变， 不变；不变；若若 变，变， 也变，但也变，但 不变不变.IILI讨论讨论exinMM 在在冲击冲击等问题中等问题中 L常量常量153-2力矩对时间的累积效应力矩对时间的累积效应 许多现象都可许多现象都可以用角动量守恒来以用角动量守恒来说明说明.花样滑冰花样滑冰跳水运动员跳水跳

9、水运动员跳水点击图片播放163-2力矩对时间的累积效应力矩对时间的累积效应 刚体对转轴的角动量守恒是经常可以见到的刚体对转轴的角动量守恒是经常可以见到的 ，如人手持哑铃的转动如人手持哑铃的转动 ,芭蕾舞演员和花样滑冰运动芭蕾舞演员和花样滑冰运动员作各种快速旋转动作员作各种快速旋转动作, 都利用了对转轴的角动量都利用了对转轴的角动量守恒定律。守恒定律。 173-2力矩对时间的累积效应力矩对时间的累积效应 常量tI tI tI 183-2力矩对时间的累积效应力矩对时间的累积效应193-2力矩对时间的累积效应力矩对时间的累积效应自然界中存在多种守恒定律自然界中存在多种守恒定律2 动量守恒定律动量守恒

10、定律2能量守恒定律能量守恒定律2角动量守恒定律角动量守恒定律2电荷守恒定律电荷守恒定律2质量守恒定律质量守恒定律2宇称守恒定律等宇称守恒定律等203-2力矩对时间的累积效应力矩对时间的累积效应例例 一均质棒，长度为一均质棒，长度为 L，质量为，质量为M，现有一子弹在距轴为，现有一子弹在距轴为 y 处水平射入细棒，子弹的质量为处水平射入细棒，子弹的质量为 m ,速度为速度为 v0 。求求 子弹细棒共同的角速度子弹细棒共同的角速度 。解解ym0v其中其中xNy0vm2231myMLIII子棒22031myMLymvr讨论讨论子弹、细棒系统的动量矩守恒子弹、细棒系统的动量矩守恒 I水平方向水平方向动

11、量守恒动量守恒213-2力矩对时间的累积效应力矩对时间的累积效应 例例2：在光滑水平桌面上放置一个静止的在光滑水平桌面上放置一个静止的质量为质量为M、长为长为2l、可绕中心转动的细杆，有可绕中心转动的细杆，有一质量为一质量为m的小球以速度的小球以速度v0与杆的一端发生完与杆的一端发生完全弹性碰撞，求小球的反弹速度全弹性碰撞，求小球的反弹速度v及杆的转动及杆的转动角速度角速度。mo解：在水平面上，碰解：在水平面上，碰撞过程中系统角动量撞过程中系统角动量守恒，守恒，LL0Ivvmlml0（1）0v223-2力矩对时间的累积效应力矩对时间的累积效应mo弹性碰撞动能守恒，弹性碰撞动能守恒，222212

12、121Immvv0（2）22312121MllMI)(其中其中0v联立联立(1)、(2)式求解式求解3mMM)v-(3mv03m)l(M6mv0233-2力矩对时间的累积效应力矩对时间的累积效应 例例3 摩擦离合器摩擦离合器 飞轮飞轮1：J1、 w1 摩擦轮摩擦轮2： J2 静止，两轮沿轴向结合，结合后两轮达到静止，两轮沿轴向结合，结合后两轮达到的共同角速度。的共同角速度。两轮对共同转轴的角动量守恒两轮对共同转轴的角动量守恒2111III2111III解：解：试与下例的齿轮试与下例的齿轮啮合过程比较。啮合过程比较。21243-2力矩对时间的累积效应力矩对时间的累积效应两轮绕不同轴转动，故对两轮

13、绕不同轴转动，故对两轴分别用角动量定理：两轴分别用角动量定理：01111dIItFr222dItFr2211rr解：解：0122F1 例例4 两圆盘形齿轮半径两圆盘形齿轮半径r1 、 r2 ，对通过盘心对通过盘心垂直于盘面转轴的垂直于盘面转轴的转动惯量为转动惯量为I1 、 I2，开始开始 1轮以轮以 转动，然后两轮正交啮合，求啮合后转动，然后两轮正交啮合，求啮合后两轮的角速度。两轮的角速度。0253-2力矩对时间的累积效应力矩对时间的累积效应得：得：22121222011rIrIrI22121221012rIrIrrI0122F101111dIItFr222dItFr2211rr263-2力矩

14、对时间的累积效应力矩对时间的累积效应 例例5 质量为质量为M，半径为，半径为R的转台，可绕通过中心的转台，可绕通过中心的竖直轴转动，设阻力可以忽略不计。质量为的竖直轴转动，设阻力可以忽略不计。质量为m的人，站在边缘上绕台奔跑一周，求相对于地面的人，站在边缘上绕台奔跑一周，求相对于地面而言，人和转台各转了多少角度。而言，人和转台各转了多少角度。273-2力矩对时间的累积效应力矩对时间的累积效应 例例6一杂技演员一杂技演员M由距水平跷板高为由距水平跷板高为h 处自由下落到跷板的一端处自由下落到跷板的一端A，并把跷板另一并把跷板另一端的演员端的演员N弹了起来问演员弹了起来问演员N可弹起多高可弹起多高? ?ll/2CABMNh283-2力矩对时间的累积效应力矩对时间的累积效应设跷板是匀质的，长度为设跷板是匀质的，长度为l，质量为质量为 ，跷板可绕中部支撑点跷板可绕中部支撑点C 在竖直平面内转动，在竖直平面内转动，演员的质量均为演员的质量均为m假定演员假定演员M落在跷板上，落在跷板上，与跷板的碰撞是与跷板的碰撞是完全非弹性完全非弹性碰撞碰撞m解解碰撞前碰撞前M落在落在 A点的速度点的速度21M)2( ghv碰撞后的瞬间，碰撞后的瞬间，M、N具有相