几何图形的计数

1、在数学竞赛试题和中考中，经常出现一些几何计数问题，所谓几何计数是指在数学竞赛试题和中考中，经常出现一些几何计数问题，所谓几何计数是指计算满足一定条件的图形的个数它的内容比较新颖有趣，为了准确计数，计算满足一定条件的图形的个数它的内容比较新颖有趣，为了准确计数，必须要有一套计数的方法，否则越数头绪越杂乱，很难得出准确的结果必须要有一套计数的方法，否则越数头绪越杂乱，很难得出准确的结果本讲将较系统地介绍初中数学中所使用的一些计数方法本讲将较系统地介绍初中数学中所使用的一些计数方法学习计数方法不仅仅使我们获得一定的数学知识和方法，更重要的是使我们学习计数方法不仅仅使我们获得一定的数学知识和方法，更重

2、要的是使我们感受到数学中的一些重要思想的运用，感受到数学中的一些重要思想的运用，如数形结合思想、分类讨论思想如数形结合思想、分类讨论思想和和转转化的思想，化的思想，分类讨论思想在这里尤其突出，我们所使用的所有计数方法都离分类讨论思想在这里尤其突出，我们所使用的所有计数方法都离不开分类不开分类 下面让我们通过例题研究和熟悉几何计数的方法吧！下面让我们通过例题研究和熟悉几何计数的方法吧！ AB、例例1数线段时，可以线段的左端点进行分类，逐类分别数出线段条数后相加数线段时，可以线段的左端点进行分类，逐类分别数出线段条数后相加AC、AD、AE、AF 共共5条条BC、BD、BE、BF共共4条条CD、CE

3、、CF共共3条条DE、DF共共2条条EF共共1条条合计有合计有5+4+3+2+1=15（条）（条）（一）数（一）数 线线 段段基础训练基础训练 1 共有共有6(6+1)2=21（条）（条）注意：这里涉及到数学中很重要的思想方注意：这里涉及到数学中很重要的思想方法法分类的思想方法。分类的思想方法。在几何计数中怎在几何计数中怎样分类？本例所介绍的是方法（样分类？本例所介绍的是方法（1）：按照）：按照包含同一图形进行分类；（包含同一图形进行分类；（2）先划分出基）先划分出基本图形，再按照包含基本图形的数目分本图形，再按照包含基本图形的数目分类类你是怎样数的？你是怎样数的？如果一条线段上有如果一条线段

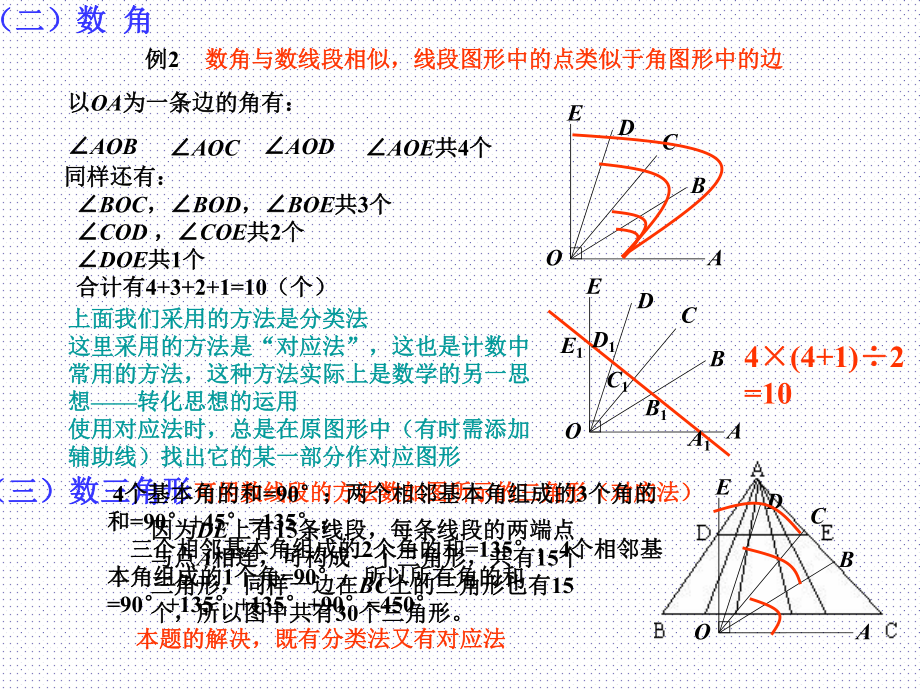
4、上有n+1个点个点(包括两个端点包括两个端点)（或含有（或含有n个个“基本线段基本线段”），那么，那么这这n+1个点把这条线段一共分成的线段总数为个点把这条线段一共分成的线段总数为n+(n-1)+2+1= . 2) 1( nnAB 、BC 、 CD 、 DE 、 EF; AC 、 BD 、 CE 、 DF；AD 、 BE 、 CF；AE 、 BF；AF共共16条条（二）数（二）数 角角例例2BACDEO数角与数线段相似，线段图形中的点类似于角图形中的边数角与数线段相似，线段图形中的点类似于角图形中的边以以OA为一条边的角有：为一条边的角有：AOBAOCAODAOE共共4个个同样还有：同样还有：

5、BOC，BOD，BOE共共3个个COD ，COE共共2个个DOE共共1个个合计有合计有4+3+2+1=10（个）（个）（三）数三角形（三）数三角形可用数线段的方法数如图所示的三角形（对应法）可用数线段的方法数如图所示的三角形（对应法）因为因为DE上有上有15条线段，每条线段的两端点条线段，每条线段的两端点与点与点A相连，可构成一个三角形，共有相连，可构成一个三角形，共有15个个三角形，同样一边在三角形，同样一边在BC上的三角形也有上的三角形也有15个，所以图中共有个，所以图中共有30个三角形。个三角形。上面我们采用的方法是分类法上面我们采用的方法是分类法这里采用的方法是这里采用的方法是“对应法

6、对应法”，这也是计数中，这也是计数中常用的方法，这种方法实际上是数学的另一思常用的方法，这种方法实际上是数学的另一思想想转化思想的运用转化思想的运用使用对应法时，总是在原图形中（有时需添加使用对应法时，总是在原图形中（有时需添加辅助线）找出它的某一部分作对应图形辅助线）找出它的某一部分作对应图形本题的解决，既有分类法又有对应法本题的解决，既有分类法又有对应法BACDEOA1B1C1D1E14(4+1)2=10 4个基本角的和个基本角的和=90；两个相邻基本角组成的；两个相邻基本角组成的3个角的个角的和和=90+45=135； 三个相邻基本角组成的三个相邻基本角组成的2个角的和个角的和=135；

7、4个相邻基个相邻基本角组成的本角组成的1个角个角=90，所以所有角的和，所以所有角的和=90+135+135+90=450BACDEO顶点为顶点为O，且，且一边在一边在AB上的三角形有上的三角形有342=6（个）；（个）；一边在一边在BC上的三角形有上的三角形有452=10（个）；（个）；一边在一边在AC上的三角形有上的三角形有 342=6（个），（个），再加再加ABC，所以共有所以共有23个三角形个三角形基础训练基础训练5 下图中共有下图中共有 个三角形个三角形 ABCO（四）数长方形、平行四边形和正方形（四）数长方形、平行四边形和正方形AM与与EB对应着长方形对应着长方形EPNB, AM与

8、与GB对应着长方形对应着长方形GQNB. 就是说就是说AM与与AB边的边的6条线段都分别对应着一个长方形，共条线段都分别对应着一个长方形，共6个长方形个长方形AD边上共有边上共有3条线段，其余两条线段条线段，其余两条线段AD和和MD也都分别对应着也都分别对应着6个长方形，个长方形，所以共有所以共有36=18个长方形个长方形ABCDEFGHQPMN图中共有图中共有-个长方形个长方形一般的，类似于这样的长方形（平行四边形），若其横边上共有一般的，类似于这样的长方形（平行四边形），若其横边上共有n条线段，条线段，纵边上共有纵边上共有m条线段，则图中共有长方形（平行四边形）条线段，则图中共有长方形（平

9、行四边形）mn个个线段线段AM与与AE对应着长方形对应着长方形AMPE，AM与与AG对应着长方形对应着长方形AMQG，AM与与AB对应着长方形对应着长方形AMNB，AM与与EG对应着长方形对应着长方形EPQG,例例4横边上有横边上有8(8+1)2=36条线段，纵边上有条线段，纵边上有7(7+1)2=28条线段，条线段，所以共有所以共有3628=1008个平行四边形个平行四边形例例6 （雨露招生试题）如图，图中平行四边形的个数为（雨露招生试题）如图，图中平行四边形的个数为 思考：能否像例思考：能否像例4那样数平行四边形？那样数平行四边形？可以将图形分割成几部分，使每一部分都像例可以将图形分割成几

10、部分，使每一部分都像例4那样的图形那样的图形但分割的块数越少越好但分割的块数越少越好3021442122）（）（思考：原图中平行四边形的个数是否等于思考：原图中平行四边形的个数是否等于60？假设分为如下图所示的两块，那么每块中的假设分为如下图所示的两块，那么每块中的平行四边形的个数都是平行四边形的个数都是思考：如最右侧的图形中也有思考：如最右侧的图形中也有30个平行四边形，个平行四边形， 那么原图中平行四边形的个数是否是那么原图中平行四边形的个数是否是330=90？不是不是90，还应减去如下图所示的两个，还应减去如下图所示的两个“田字格田字格”中的各中的各9个平行四边形，因为这个平行四边形，因

11、为这18个个平行四边形已经包含在前平行四边形已经包含在前60个之中个之中所以，原图形中平行四边形的个数是所以，原图形中平行四边形的个数是9018=72注意：在使用分类计数法时，一定要注意是否有遗漏或重复计数的！注意：在使用分类计数法时，一定要注意是否有遗漏或重复计数的！例例5 如左、中、右三图，各包含多少个正方形？如左、中、右三图，各包含多少个正方形？ 为便于叙述，我们设一个小正方形的边长为为便于叙述，我们设一个小正方形的边长为1，那么，那么左图中边长为左图中边长为1的正方形的个数是的正方形的个数是 32=6边长为边长为2的正方形的个数是的正方形的个数是21=2所以左图中共有正方形所以左图中共

12、有正方形 32+21=8（个）（个）中图中边长为中图中边长为1的正方形的个数是的正方形的个数是43=12边长为边长为2的正方形的个数是的正方形的个数是32=6边长为边长为3的正方形的个数是的正方形的个数是21=2所以中图中共有正方形所以中图中共有正方形 43+32+21=20（个）（个） 右图中边长为右图中边长为1的正方形的个数是的正方形的个数是64=24边长为边长为2的正方形的个数是的正方形的个数是53=15边长为边长为3的正方形的个数是的正方形的个数是42=8边长为边长为4的正方形的个数是的正方形的个数是31=3所以中图中共有正方形所以中图中共有正方形 64+54+42+31=50（个）（

13、个） 如果一横行有如果一横行有m个小正方形，一竖行有个小正方形，一竖行有n个（假设个（假设mn）小正方形，）小正方形，那么图中正方形的个数是那么图中正方形的个数是mn+(m1)(n1)+(mn+1)(nn+1) 这里所采用的方法是分类这里所采用的方法是分类法中的另一种，是：法中的另一种，是：（3）按照图形的大小分类）按照图形的大小分类例例7ABCKDEFGHL第第1类：与三角形类：与三角形ABE形状有某些相似的三角形有形状有某些相似的三角形有个个你打算怎样数图中的三角形？你打算怎样数图中的三角形？5第第2类：与三角形类：与三角形ABF形状有某些相似的三角形有形状有某些相似的三角形有个个5第第3

14、类：与三角形类：与三角形ABG形状有某些相似的三角形有形状有某些相似的三角形有个个10第第4类：与三角形类：与三角形ACD形状有某些相似的三角形有形状有某些相似的三角形有个个5第第5类：与三角形类：与三角形AFL形状有某些相似的三角形有形状有某些相似的三角形有个个55第第6类：与三角形类：与三角形AGD形状有某些相似的三角形有形状有某些相似的三角形有个个所以图中的三角形共有所以图中的三角形共有3535个个这里所采用的方法是分类法中的另一种，是：这里所采用的方法是分类法中的另一种，是：（4）按照图形的形状分类）按照图形的形状分类也可以说是也可以说是（5）按照图形所处的位置分类）按照图形所处的位置

15、分类 例例8（华罗庚金杯竞赛题）下图中有（华罗庚金杯竞赛题）下图中有 个正方形，有个正方形，有 个三角形个三角形能否将图中的正方形分类，按照不同类型分别数能否将图中的正方形分类，按照不同类型分别数出其中的正方形个数？出其中的正方形个数？66+55+44+33+22+11=91除上一类为，还有除上一类为，还有 个正方形个正方形4 共有共有95个正方形个正方形这里所使用的方法是分类法中的（这里所使用的方法是分类法中的（4）按照图形的形状分类）按照图形的形状分类662=72个个直角边长为直角边长为1的三角形有的三角形有1-2行行 2-3行行3-4行行4-5行行5-6行行 直角边长为直角边长为2的三角

16、形的三角形8个个,6个个,2个个,8个个, 6个个,共共30个个4个个,2个个直角边长为直角边长为3的三角形的三角形 1-2行行3-5行行4-6行行4个个,共共10个个思考：还有漏数的三角形吗？思考：还有漏数的三角形吗？各各4个个,共共12个个3个个1个个斜边长为斜边长为2的三角形的三角形1-3行行第第4行行第第5行行第第6行行 4个，共计个，共计20个个1-6列依次列依次3+3+3+2+3+3=17（个）（个） 思考：还有漏数的三角形吗？思考：还有漏数的三角形吗？思考：还有漏数的三角形吗？思考：还有漏数的三角形吗？斜边长为斜边长为4的三角形的三角形直角边长为直角边长为4的三角形的三角形3-6

17、行行2个个所以图中的三角形共计所以图中的三角形共计72+30+10+2+20+17+4=155（个）（个）这里用了分类法中的（这里用了分类法中的（3）按照图形的大小分类（之后又按图形所处位置分类）按照图形的大小分类（之后又按图形所处位置分类）1-4行行1个个 ,2-5行行2个，个， 4-5行行1个，共个，共4个个分为两类，一类是有一组对边在水平方向的正分为两类，一类是有一组对边在水平方向的正方形，如左图方形，如左图 这类正方形的个数是这类正方形的个数是课后反思总结课后反思总结计数方法：计数方法： 1分类计数法分类计数法 （1）按照包含同一图形分类；）按照包含同一图形分类； （2）按照图形所包含

18、的）按照图形所包含的“基本图形基本图形”的个数分类。的个数分类。 （3）按照图形的大小分类；）按照图形的大小分类； （4）按照图形的形状分类；）按照图形的形状分类； （5）按照图形所处的位置分类）按照图形所处的位置分类 2对应计数法对应计数法 几个计算公式：几个计算公式： 1线段、角的计数公式：线段、角的计数公式： 2长方形、平行四边形的计数公式：长方形、平行四边形的计数公式：横边上共有横边上共有n条线段，条线段，纵边上共有纵边上共有m条线段，则图中共有长方形（平行四边形）条线段，则图中共有长方形（平行四边形）mn个个 3正方形的计数公式：正方形的计数公式：如果一横行有如果一横行有m个小正方形

19、，一竖行有个小正方形，一竖行有n个（假个（假设设mn）小正方形，那么图中正方形的个数是）小正方形，那么图中正方形的个数是 mn+(m1)(n1)+(mn+1)(nn+1) = mn+(m1)(n1)+(mn+1)12) 1( nn图形个数问题解答在问题解答在http:/ 说出你是怎样数的说出你是怎样数的BCDEFGA与数长方形和正方形的方法类似与数长方形和正方形的方法类似长方体有长方体有个个(3+2+1)(2+1)(2+1)=54正方体有正方体有个个322+211=147如图，图中的三角形共有多少个？请把它们都用记号表示出来如图，图中的三角形共有多少个？请把它们都用记号表示出来MBCDEFGN

20、A(1)一边在一边在AB上的三角形有上的三角形有ABC, ABE,ABN,ABF,ADM,ADC,BDG,BDC(2)一边在一边在BC上而另一边上而另一边 不在不在AB上的三角形有上的三角形有BCA, BCD,BCF,BCG,BEA,BEN,ECA,ECM(3)一边在一边在CA上而另一边既上而另一边既不在不在AB上也不在上也不在BC上的三角形有上的三角形有CAB, CAD, CAE,CAM,CFB , CFG, AFB, AFN(4)三边不在三边不在AB、BC、CA上的有上的有MNG所以图中的三角形共有所以图中的三角形共有8+5+3+1=17个个共计共计8+5+3=16个吗？个吗？3(4+3+

21、2+1)（4+3+3+1）=100图中共有直线图中共有直线6条，设为条，设为a, b,c,d,e,f, 每每3条一组，列表如下条一组，列表如下abc abd abe abf acd ace acf ade adf aef 计计10组组bfcedabcd bce bcf bde bdf bef 计计6组组cde cdf cef计计3组组def 计计1组组 这里采用的是对应法，但是也要注意计数中是否有遗漏或重复这里采用的是对应法，但是也要注意计数中是否有遗漏或重复def 计计1组组 ，合计，合计10+6+3+1=20组组但是经过同一点的三条直线不能围成三角形，但是经过同一点的三条直线不能围成三角形

22、，所以图中的三角形共有所以图中的三角形共有203=17（个）（个）提高训练提高训练3图中共有多少个三角形？图中共有多少个三角形？显然三角形可分为尖向上与尖向下两大类，两类中三显然三角形可分为尖向上与尖向下两大类，两类中三角形的个数相等尖向上的三角形又可分为角形的个数相等尖向上的三角形又可分为6类类（1）最大的三角形最大的三角形1个个(即即ABC)，（2）第二大的三角形有）第二大的三角形有 1+2=3（个）（个）（3）第三大的三角形有）第三大的三角形有 1+2+3=6（个）（个）（4）第四大的三角形有）第四大的三角形有 1+2+3+4=10（个）（个）（5）第五大的三角形有）第五大的三角形有 1

23、+2+3+4+5=15（个）（个）（6）最小的三角形有）最小的三角形有1+2+3+4+5+6+3=24（个）（个）最后加的最后加的3个是哪个是哪3个？个？所以尖向上的三角形共有所以尖向上的三角形共有1+3+6+10+15+24=59（个）（个）图中共有三角形图中共有三角形259=118（个）（个）提高训练提高训练4 在在88的方格棋盘中，取出一个由三个小方格组成的的方格棋盘中，取出一个由三个小方格组成的“L”形形（如图），一共有多少种不同的方法？（如图），一共有多少种不同的方法？ 注意：数注意：数“不规则几何图形不规则几何图形”的个数时，常用对应法的个数时，常用对应法第第1步：找对应图形步：找对应图形 每一种取法，有一个点与之对应，每一种取法，有一个点与之对应，这就是图中的这就是图中的A点，它是棋盘上横线与竖线的交点，且不点，它是棋盘上横线与竖线的交点，且不在棋盘边上。在棋盘边上。第第2步：明确对应关系步：明确对应关系从下图可以看出，棋盘内的每一从下图可以看出，棋盘内的每一个点对应着个点对应着4个不同的取法（个不同的取法（“L”形的形的“角角”在在22正方正方形的不同