固体物理黄昆2

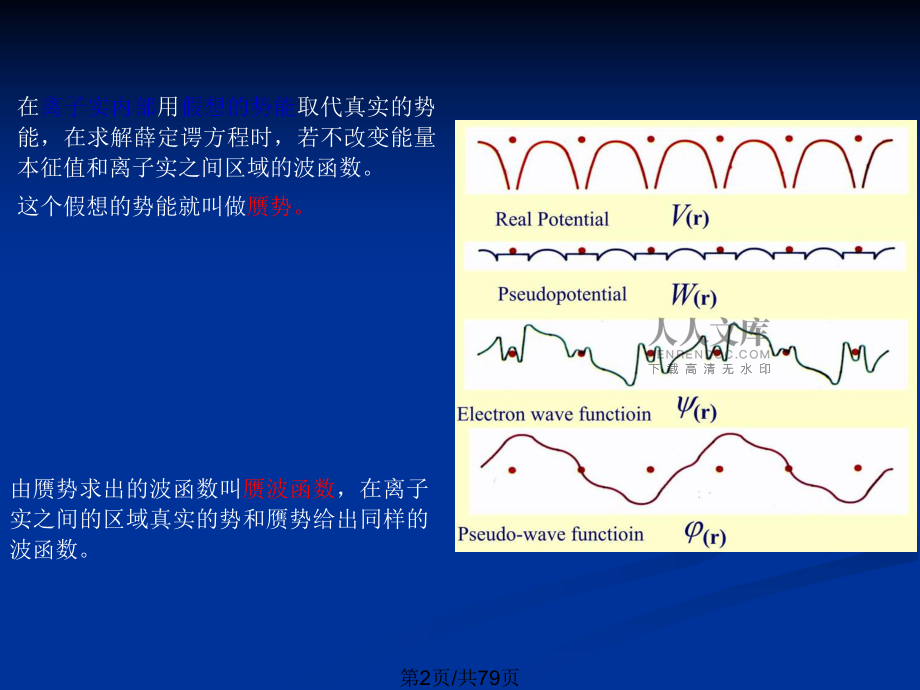
1、会计学1固体物理黄昆固体物理黄昆2第1页/共79页在离子实内部用假想的势能取代真实的势能，在求解薛定谔方程时，若不改变能量本征值和离子实之间区域的波函数。这个假想的势能就叫做赝势。由赝势求出的波函数叫赝波函数，在离子实之间的区域真实的势和赝势给出同样的波函数。第2页/共79页近自由电子近似认为原子实对电子的作用很弱，电子的运动基本上是自由的。其结果主要适用于金属的价电子。当晶体中原子的间距较大，原子实对电子有相当强的束缚作用。当电子距某个原子实较近时，电子的运动主要受该原子势场的影响，这时电子的行为与孤立原子中电子的行为相似。这时，可将孤立原子看成零级近似，将其他原子势场的影响看成小的微扰。此

2、方法称为紧束缚近似 (TBA)。紧束缚近似方法的一个突出优点是它可以把晶体中电子的能带结构与构成这种晶体的原子在孤立状态下的电子能级联系起来。第3页/共79页电子在格矢处原子附近运动考虑简单晶格情况。332211amamamRm 电子的孤立原子束缚态波函数)(miRr )()()(222miimimRrRrRrVm ：Rm格点的原子势场格点的原子势场 ：某原子能级：某原子能级（非简并）（非简并） )(mRrV i 第4页/共79页)()()(222rErrUm 晶体中电子的波函数 满足的薛定谔方程：晶体的周期性势场，即各格点原子的势场之和：微扰项)(r )(rU)()()()()()(222r

3、ErRrVrUrRrVmmm )()(mRrVrU 原子轨道线性组合法：（LCAO）微扰以后的状态是N个简并态的线性组合，即用原子轨道的线性组合来构成晶体中电子共有化的轨道。 mmimRrar)()( 第5页/共79页将晶体中电子波函数 代入薛定谔方程)(r )()()()()()(222rErRrVrUrRrVmmm mmimmmimimRraERrRrVrUa)()()()( 当原子间距比原子半径大时，不同格点的原子束缚态波函数重叠很小，近似为nmnimirdRrRr )()(*正交关系简化计算。第6页/共79页即 mnimimnimaErdRrRrVrURra)()()()()(* mm

4、immmimimRraERrRrVrUa)()()()( 以 左乘上面方程)(*niRr nmmimninmimEardRrRrVrURra )()()()(* 因 有N种可能选取办法，故方程是N个联立方程中的一个方程。)(*niRr 第7页/共79页 mnimimnimaErdRrRrVrURra)()()()()(* 改变变量，令考虑到势场U为周期函数)()()()()(*mnimniRRJdVURR 积分只决定于相对位置mRr )(mnRR J函数前面加负号的原因是，周期场减去原点的原子场，仍为负值。 mnimnmaERRJa)()( 第8页/共79页 周期性势场减去原子的势场，仍为负值

5、)()(VU)()()()()(*mnimniRRJdVURR第9页/共79页 mnimnmaERRJa)()( am只由 来决定mRk imCea 方程具有简单形式的解)(mnRR sRk isise )R(JE为任意常数矢量mnsRRR kmmiRk ikRreNrm)(1)(对于确定的 k晶体中电子的波函数:容易验证，晶体中电子的波函数是布洛赫函数。第10页/共79页 sRk isiseRJkE)()( 能量本征值考虑周期性边界条件，考虑周期性边界条件， 的取值为的取值为 k123123123hhhNNN kbbbh1, h2, h3整数整数由此可知，在简约区中，波矢由此可知，在简约区中

6、，波矢 共有共有N个准连续的取个准连续的取值，即可得值，即可得N个电子的本征态个电子的本征态 k(r)对应于对应于N个准连续个准连续的的k值。这样，值。这样，E(k)将形成一个将形成一个准连续的能带准连续的能带。 k形成固体时，一个原子能级将展宽为一个相应的能带，其Bloch函数是各格点上原子波函数 的线性组合jrR第11页/共79页 j(r-Rs)和和 j(r)表示相距为表示相距为Rs的格点上的原子波函数，的格点上的原子波函数，显然积分值只有当它们显然积分值只有当它们有一定相互重叠有一定相互重叠时，时，才不为零才不为零只保留到近邻项，而略去其他影响小的项，只保留到近邻项，而略去其他影响小的项

7、，能量本征值能量本征值E(k)的表达式可进一步简化：的表达式可进一步简化：当Rs 0时，两波函数完全重叠 NearestRRk isisseRJJkE)()(0 dVUJii )()()()(*0 dVURRJisis )()()()()(* 第12页/共79页1：求简单立方晶体中由原子的：求简单立方晶体中由原子的s态所形成的能带态所形成的能带aa由于由于s态的原子波函数是态的原子波函数是球对称球对称的，有的，有1sJJR对于简单立方：对于简单立方： 01yyxxzzik aik aik aik aik aik asEJJeeeeee k012coscoscossxyzJJk ak ak as

8、R近邻格矢近邻格矢( a, 0, 0), (0, a, 0), (0, 0, a)sR第13页/共79页在简单立方晶格的简约区中在简单立方晶格的简约区中 016sEJJ 由于由于s态波函数是偶宇称，态波函数是偶宇称， s(r)= s(-r)， 所以，在所以，在近邻重叠积分中波函数的贡献为正，即近邻重叠积分中波函数的贡献为正，即J1 0 MXRkxkykz 点：点： (0, 0, 0) k012sE XJJX点：点： ( /a, 0, 0) k 016sE RJJR点：点： ( /a, /a, /a) k012coscoscossxyzJJk ak ak a第14页/共79页 点：能带底；点：能

9、带底；R点：能带顶点：能带顶 112EE REJ 能带宽度：原子的一个s能级在晶体中展宽为一个相应的能带，能带宽度取决于J1，即近邻原子波函数的重叠积分 原子的内层电子轨道半径较小，所形成的能带校窄；而外层电子轨道半径较大，所形成的能带较宽以上讨论仅适用于原子能级非简并，且原子波函数重叠很少的情况，即适用于原子内层 s电子所形成的能带J0 s12J1E第15页/共79页对于对于p电子、电子、d电子电子等，这些状态都是等，这些状态都是简并简并的，因此，的，因此，其其Bloch函数应是孤立原子的有关状态波函数的线函数应是孤立原子的有关状态波函数的线性组合性组合求简单立方晶体由原子的求简单立方晶体由

10、原子的p态所形成的能带态所形成的能带原子的原子的p态为态为三重简并三重简并，其原子轨道可表为，其原子轨道可表为在简单立方晶体中，在简单立方晶体中，三个三个p轨道各自形成一个能轨道各自形成一个能带带，其，其波函数是各自原子轨道的线性组合波函数是各自原子轨道的线性组合 xyzpppxf ryf rzf r第16页/共79页由于由于p轨道不是球对称轨道不是球对称的，因此，沿不同方向的的，因此，沿不同方向的近邻近邻重叠积分重叠积分J(Rs)不完全相同不完全相同。如。如 ：电子主：电子主要集中在要集中在x轴方向，在六个近邻重叠积分中，沿轴方向，在六个近邻重叠积分中，沿x轴方向的重叠积分较大，用轴方向的重

11、叠积分较大，用J1表示；沿表示；沿y方向和方向和z方向的重叠积分用方向的重叠积分用J2表示表示其它两个方向类似其它两个方向类似xpxxyyzzipppipippCeCeCe k Rkk Rkk RkrRrRrR第17页/共79页 0122cos2coscosxppxyzEJJk aJk ak a k 0122cos2coscosyppyzxEJJk aJk ak a k 0122cos2coscoszppzxyEJJk aJk ak a kxy Xs带带px带带py、pz带带E(k)原子的原子的p态是态是奇宇称奇宇称： xxppxx xp沿x轴方向的重叠积分J1 0第18页/共79页 1. 对

12、于原子的对于原子的内层电子内层电子，其电子，其电子轨道很小，因而形成的能带较轨道很小，因而形成的能带较窄。这时，窄。这时，原子能级与能带之原子能级与能带之间有简单的一一对应关系间有简单的一一对应关系 E这时，原子能级与能带之间比较复杂，不一定有简单的一一对应关系。一个能带不一定与孤立原子的某个能级相对应，可能会出现能带的重叠 2. 对于外层电子，由于其电子轨道较大，形成的能带就较宽第19页/共79页在某些情况下还可能出现在某些情况下还可能出现不同原子态的相互作用不同原子态的相互作用。如：如：Si的价带与导带的价带与导带紧束缚近似紧束缚近似对原子的对原子的内层电子是相当好的近似内层电子是相当好的

13、近似，它，它还可用来近似地描述过渡金属的还可用来近似地描述过渡金属的d带、类金刚石晶体带、类金刚石晶体以及惰性元素晶体的价带。紧束缚近似是定量计算以及惰性元素晶体的价带。紧束缚近似是定量计算绝缘体、化合物及半导体特性的有效工具绝缘体、化合物及半导体特性的有效工具3p3ssp3成键态成键态反键态反键态导带导带价带价带第20页/共79页紧束缚近似中，能带中电子波函数可写成布洛赫函数和对于任何能带Wannier 函数1()( , )nik RnnnkkW rRek rN 一个能带的Wannier 函数是由同一个能带的布洛赫函数所定义 nniRk iikRreNrkn)(1),( nnnRk inkR

14、rWeNrkn)(1),( 第21页/共79页瓦尼尔函数满足正交关系1.紧束缚近似中，如果近似忽略原子波函数的交叠，瓦尼尔函数就是孤立原子的波函数。2. 如果能带情况和紧束缚近似相差很远，瓦尼尔函数将很少保留孤立原子波函数的信息，但它仍然比较定域化。在讨论电子空间定域性起重要作用的问题时，瓦尼尔函数工具比较方便。 ,*)()(mmmnmnrdRrWRrW 第22页/共79页 1Tffrr一、一、 对称操作对称操作晶体点群的对称操作算符晶体点群的对称操作算符T( )，物理意义：对于，物理意义：对于任意函数任意函数 ，有，有 fr -1: 的逆操作的逆操作定义定义: 点经点经 操作后变换到操作后变

15、换到 点点 1rr nnEE kk上式对所有晶体点群的对称操作 都成立在在 空间中空间中 具有与晶体点群完全相同的具有与晶体点群完全相同的对称性对称性 k nE k第23页/共79页三、 能带关于k的周期性 )2()(ankEkE 三维情况中表示（对同一能带成立）)()(kEkE )()(nGkEkE 第24页/共79页1) 简约布里渊区图象 所有能带在简约布里渊区内给出i) 它属于哪一个能带ii) 它的简约波矢 是什么k简约布里渊区标志一个状态第25页/共79页在每一个布里渊区画出所有能带，构成k空间中能量分布的完整图像第26页/共79页不同能带绘于k空间中不同的布里渊区中IIIIIIIII

16、II第27页/共79页一、能态密度一、能态密度1. 定义定义能态密度：能态密度： dZN EdEdSdk kxkyEE+dEdZ：能量在：能量在EE+dE两等能面间的能两等能面间的能态数（考虑了电子自旋）态数（考虑了电子自旋）能态密度能态密度：能带中：能带中单位能量间隔内的电子能态数单位能量间隔内的电子能态数dZ=2 (k) (k空间中能量在空间中能量在EE+dE两等能面间的体积两等能面间的体积)328VdSdk等能面dEEdk k第28页/共79页 34dZVdSN EdEE k2. 近自由电子的能态密度近自由电子的能态密度对于自由电子：对于自由电子： 22(0)2kEm k能量为能量为E的

17、等能面是半径为的等能面是半径为22mEk 在球面上在球面上2dEEkdkm k的球面第29页/共79页 33244VdSVmN EdSkE k3223223122442VmVmkEk在在近自由电子情况近自由电子情况下，下，周期场的影响周期场的影响主要表现主要表现在布里渊在布里渊区边界附近区边界附近，而离布里渊区边界较远处，周期场对电子，而离布里渊区边界较远处，周期场对电子运动的影响很小。运动的影响很小。 波矢接近布里渊区的A点，能量受到周期性的微扰而下降，等能面向边界凸现在A点到C点之间，等能面不再是完整的闭合面，而是分割在各个顶点附近的曲面。第30页/共79页近自由电子的能态密度近自由电子的

18、能态密度EA近自由电子的等能面近自由电子的等能面kxkyAC随着k接近布里渊区，等能面不断向边界凸现，两个等能面之间的体积不断增大，能态密度将显著增大。在A点到C点之间，等能面发生残缺，达到C点时，等能面缩成一个点。能态密度不断减小直到为零。第31页/共79页N(E)EECEBN(E)EECEB当EC EB时：出现时：出现能带重叠能带重叠 第二布里渊区能态密度能量E越过第一布里渊区的A点，从B点开始能态密度由零迅速增大。第32页/共79页以简单立方晶格以简单立方晶格s带为例带为例: 012coscoscossxyzEEJk ak ak a k00sEJ 在在k=0，即能带底附近，即能带底附近，

19、等能面近似为球面等能面近似为球面 随着随着E的增大的增大，等能面明，等能面明显显偏离球面偏离球面第33页/共79页N(E)E0E06J1E02J1E0+6J1E0+2J1E()E(X)E(M)E(R)12sin,sin,sinxyzEaJk ak ak a k22212sinsinsinxyzEaJk ak ak ak 1/222231sinsinsin8xyzVN Ek ak ak adSaJ在在 、X、M和和R点处，点处，kE =0，称为，称为Van Hove奇点，这些点都奇点，这些点都是布里渊区中的高对是布里渊区中的高对称点称点第34页/共79页3) 紧束缚模型的电子能态密度 简单立方格

20、子的s带 等能面为球面k=0附近)coscos(cos2)(10akakakJEkEzyxs)(2)(222*2minzyxkkkmEkE 随着E的增大，等能面与 近自由电子的情况类似第35页/共79页32221( )8(sinsinsin)xyzVdSN EaJk ak ak a等能面能态密度)sinsin(sin22221akakakaJEzyxk)coscos(cos2)(10akakakJEkEzyxsEdSVENk34)(第36页/共79页X点k = (/a, 0, 0)的能量102JEEX出现微商不连续的奇点 等能面与布里渊区相交带底106JEE102JEE和)sinsin(sin

21、22221akakakaJEzyxk第37页/共79页102JEEX0EE 第38页/共79页2. 费米面 固体中有N个自由电子，按照泡利原理它们基态是由N 个电子由低到高填充的N个量子态mkkE2)(223334)2(2FkVN3/13/1)()83(2VNkF3/1)83(2nkF电子的能级N个电子在k空间填充一个半径为kF的球，球内包含N个状态数球的半径第39页/共79页费米波矢、费米动量、费米速度和费米温度 费米能量222FFkEm费米球半径2FFmEk 费米动量2FFpmE费米速度FFkpmpvFF费米温度BFFkET 第40页/共79页自由电子球半径rs3341srnNV3/1)4

22、3(nrs1.92srsmarmpvsFF/10/20. 460ma-10010529. 0222FFkEm20)/(1 .51areVEsF343srn3/1)83(2nkF: 1.515FEeVeV23310/ncm62/0ars第41页/共79页 晶体中的电子 满带 电子占据了一个能带中所有的状态空带 没有任何电子占据（填充）的能带导带 一个能带中所有的状态没有被电子占满 即不满带，或说最下面的一个空带价带 导带以下的第一个满带，或最上面的一个满带禁带 两个能带之间，不允许存在的能级宽度，或带隙 第42页/共79页 单电子的能级由于周期性势场的影响而形成一系列的准连续的能带，N个电子填充

23、这些能带中最低的N个状态半导体和绝缘体 电子刚好填满最低的一系列能带，形成满带，导带中没 有电子 半导体带隙宽度较小 1 eV 绝缘体带隙宽度较宽 10 eV第43页/共79页金属 电子除了填满一系列的能带形成满带，还部分填充 了其它能带形成导带 电子填充的最高能级为费密能级，位于一个或几个能 带范围内 在不同能带中形成一个占有电子与不占有电子区域 的分界面 面的集合称为费密面第44页/共79页第45页/共79页碱金属 具有体心立方格子，每个原胞内有一个原子，由N个原子构成的晶体，各满层电子的能级相应地分成2N个量子态的能带，内层电子刚好填满了相应的能带 ns态所对应的能带可以填充2N电子，N

24、个原子只有N 个自由电子，只填充了半个能带而形成导带 碱金属中的N个电子只填充了半个布里渊区，费密球 与布里渊区边界不相交，费米面接近球面 第46页/共79页二价碱土金属 最外层2个s态电子，似乎刚好填充满和s相应的能带。由于与s对应的能带和上面的能带发生重叠，2N个尚未填充满s态能带，就开始填充上面的能带，形成两个能带都是部分填充 第一布里渊区中的状 态尚未填满，第二布 里渊区已填充电子， 此时的费米面由两部 分构成 碱土金属为金属导体第47页/共79页金刚石结构的IVB族元素C、Si和Ge电子的填充 IVB原子外层有4个电子，形成晶体后成键态对应4个能带在下面，反键态对应4个能带在上面。每

25、个能带可容纳2N个电子，成键态的4个能带刚好可以容纳8N电子 金刚石结构晶体中每个原胞有两个原子，共8个电子。晶体中的8N个电子全部填充在成键态的4个能带中形成满带，反键态则是空带, 金刚石为绝缘体 Si和Ge为半导体第48页/共79页 能态密度的实验结果X射线可以将原子内层电子激发，产生空的内层能级，当外层电子(导带中的电子)跃迁填充内层能级时发射X射线光子用X射线将Na原子的内层电子激发产生诸如1s、2s和3p等空的内层能级 K: 电子到1s能级的跃迁 LI:电子到2s能级的跃迁 LII:电子到2p能级的跃迁 LIII:电子到3s能级的跃迁第49页/共79页 导带中电子能量从带底能量到最高

26、能量E0，各种能量 的电子均可发生跃迁产生不同能量的X光子 发射出X光子能量形成一个连续能量谱 发射的X光子能量可以通过实验测得X光子发射强度决定于（能态密度）（发射几率） 根据不同固体的X光子 发射谱可以获知能态密 度的信息第50页/共79页金属Na、Mg、Al和非金属金刚石、硅的实验结果第51页/共79页 在低能量区域Na、Mg、Al和金刚石、硅的X光子发射能量逐渐上升的 反映了电子的能量从带底逐渐增大，其能态密度逐渐 增大的规律第52页/共79页 在高能量的一端金属Na、Mg、Al的X光子发射谱陡然下降 反映了导带未被电子填充满，最高能量的电子对应的 能态密度最大第53页/共79页 在高

27、能量的一端金刚石、硅的X光子发射谱逐渐下降 反映了电子填充了导带中所有的状态，即满带。而在满带顶对应的布里渊区附近，电子的能态密度逐渐降为零近自由电子的能态密度近自由电子的能态密度EA近自由电子的等能面近自由电子的等能面kxkyAC第54页/共79页讨论近自由电子的费米面结构讨论近自由电子的费米面结构:对金属：对金属：EkBT，在，在T0时，时，只有费米面附只有费米面附近的少量电子受到热激发近的少量电子受到热激发FBFBFFkk TTkk TT在室温下，这个比值约为在室温下，这个比值约为102，因此，可以认，因此，可以认为金属的费米面基本上与为金属的费米面基本上与T无关无关费米半径的相对变化第

28、55页/共79页a. 费米面的构造步骤费米面的构造步骤 根据根据晶体结构晶体结构画出倒易空间中扩展的画出倒易空间中扩展的布里渊布里渊区图形区图形； 按按电子浓度电子浓度求出相应的求出相应的费米半径费米半径，并作出，并作出费费米球（圆）；米球（圆）； 将处在各个布里渊区中的将处在各个布里渊区中的费米球（圆）分块费米球（圆）分块按倒格矢按倒格矢平移到简约区平移到简约区中，来自第中，来自第n个布里渊个布里渊区的对应于第区的对应于第n个能带个能带，于是在简约区中得到，于是在简约区中得到对应于对应于各个能带的费米面图形各个能带的费米面图形； 按照按照近自由电子作必要的修正近自由电子作必要的修正第56页/

29、共79页v 电子的能量只在布里渊区边界附近偏离自由电子的能量只在布里渊区边界附近偏离自由电子能量，周期场的影响使等能面在布里渊电子能量，周期场的影响使等能面在布里渊区边界面附近发生畸变，形成向外突出的凸区边界面附近发生畸变，形成向外突出的凸包；包；v 等能面几乎总是与布里渊区边界面垂直相交；等能面几乎总是与布里渊区边界面垂直相交；v 费米面所包围的总体积仅依赖于电子浓度，费米面所包围的总体积仅依赖于电子浓度，而不取决于电子与晶格相互作用的细节；而不取决于电子与晶格相互作用的细节；v 周期场的影响使费米面上的尖锐角圆滑化周期场的影响使费米面上的尖锐角圆滑化第57页/共79页证明在一般情况下，等能

30、面与布里渊区边界面垂直相交证明在一般情况下，等能面与布里渊区边界面垂直相交-nnEEkk kknnnEEkk kk G12n kG在布里渊区边界面上：En(k)具有具有反演对称性反演对称性： nnEE kkEn(k)的的平移对称性平移对称性： nnnEE kkG在布里渊区边界面附近：在布里渊区边界面附近： kkk第58页/共79页沿布里渊区边界面的法线方向上，沿布里渊区边界面的法线方向上，1122nnnnEEkk GG-nnEEkk kknnnEEkk kk G11220nnnnEEkk GG如果沿一个边界面的法线方向上处处都有如果沿一个边界面的法线方向上处处都有120nnEk G那么，与该边

31、界面相交的那么，与该边界面相交的等能面必与此边界面垂直等能面必与此边界面垂直1122nnnnEEkk GG第59页/共79页例：二维正方晶格近自由电子的费米面图形例：二维正方晶格近自由电子的费米面图形设二维晶格的晶格常数为设二维晶格的晶格常数为a，晶体的原胞数为，晶体的原胞数为N，设平均每个原子有设平均每个原子有 个价电子，即个价电子，即电子浓度电子浓度为为 电电子子/原子原子 2222222242FFFNaNaNkkk k11222Fkkaa对于简单晶格： 224Na k的分布密度：的分布密度： k第60页/共79页其中其中1ka为简约区的内切圆半径为简约区的内切圆半径电子浓度电子浓度 kF

32、/k110.79821.12831.38241.59651.78461.954kxky第61页/共79页0K时，固体中有N个自由电子，按照泡利原理它们基态是由N个电子由低到高填充的N个量子态。3/1)83(2 nkF 电子的能级N个电子在k空间填充一个半径为kF的球，球内包含N个状态数3/13/1)()83(2VNkF 球的半径 此球面称为费米面。mkkE2)(22 3334)2(2FkVN 第62页/共79页费米波矢 、费米能、费米动量、费米速度和费米温度 费米能量费米球半径费米动量费米速度费米温度FkmkEFF222 FFmEk2 FFFFkpmEp ,2mpvFF BFFkET 第63页

33、/共79页自由电子球半径rs: 1.515FEeVeV3341srnNV 343srn 电子密度电子密度n3/1)43(nrs sFrnk92. 1)83(23/1 ma-10010529. 0 62/0 ars氢原子基态玻尔半径氢原子基态玻尔半径32223/cm10-10:n2022)/(1 .512areVmkEsFF smarmpvsFF/10/20. 460 第64页/共79页1.满带：电子占据了一个能带中所有的状态2.空带：没有任何电子占据（填充）的能带3.导带：一个能带中所有的状态没有被电子占满，即不满带，或说最下面的一个空带4.价带：导带以下的第一个满带，或最上面的一个满带5.禁

34、带：两个能带之间，不允许存在的能级宽度，或带隙 基态填充情况满带空带 对应于绝缘体和半导体满带导带 对应于金属第65页/共79页单电子的能级由于周期性势场的影响而形成一系列的准连续的能带，N个电子填充这些能带中最低的N个状态半导体和绝缘体电子刚好填满最低的一系列能带，形成满带，导带中没有电子。 半导体带隙宽度较小 1 eV 绝缘体带隙宽度较宽 10 eV金属：电子除了填满一系列的能带形成满带，还部分填充了其它能带形成导带。电子填充的最高能级为费密能级，位于一个或几个能带范围内。在不同能带中形成一个占有电子与不占有电子区域的分界面。面的集合称为费密面。第66页/共79页碱金属 ：具有体心立方格子

35、，每个原胞内有一个原子，由N个原子构成的晶体，各满层电子的能级相应地分成2N个量子态的能带，内层电子刚好填满了相应的能带。最外层 ns态所对应的能带可以填充2N电子，N个原子只有N个自由电子，只填充了半个能带而形成导带。碱金属中的N个电子只填充了半个布里渊区，费密球与布里渊区边界不相交，费米面接近球面。二价碱土金属 ：最外层2个s态电子，似乎刚好填充满和s相应的能带。由于与s对应的能带和上面的能带发生重叠，2N个尚未填充满s态能带，就开始填充上面的能带，形成两个能带都是部分填充。碱土金属为金属导体。第一布里渊区中的状态尚未填满，第二布里渊区已填充电子，此时的费米面由两部分构成。第67页/共79

36、页IVB原子外层有4个电子，形成晶体后成键态对应4个能带在下面，反键态对应4个能带在上面。每个能带可容纳2N个电子，成键态的4个能带刚好可以容纳8N电子。金刚石结构晶体中每个原胞有两个原子，共8个电子。晶体中的8N个电子全部填充在成键态的4个能带中形成满带，反键态则是空带, 金刚石为绝缘体。Si和Ge为半导体。第68页/共79页X射线可以将原子内层电子激发，产生空的内层能级，当外层电子（导带中的电子）跃迁填充内层能级时发射X射线光子。用X射线将Na原子的内层电子激发产生诸如1s、2s和3p等空的内层能级。K: 电子到1s能级的跃迁LI:电子到2s能级的跃迁LII:电子到2p能级的跃迁LIII:

37、电子到3s能级的跃迁1s2s2p价电子价电子能能 带带KL1L2第69页/共79页导带中电子能量从带底能量到最高能量E0，各种能量的电子均可发生跃迁产生不同能量的X光子。发射出X光子能量形成一个连续能量谱。发射的X光子能量可以通过实验测得。X光子发射强度决定于（能态密度）（发射几率）根据不同固体X光子发射谱可以获知能态密度信息。在低能量区域：Na、Mg、Al和金刚石、硅的X光子发射能量逐渐上升的，反映了电子的能量从带底逐渐增大，其能态密度逐渐增大的规律。第70页/共79页第71页/共79页在高能量的一端：金属Na、Mg、Al的X光子发射谱陡然下降。反映了导带未被电子填充满，最高能量的电子对应的能态密度最大。金刚石、硅的X光子发射谱逐渐下降。反映了电子填充了导带中所有的状态，即满带。而在满带顶对应的布里