高中数学课件曲边梯形的面积

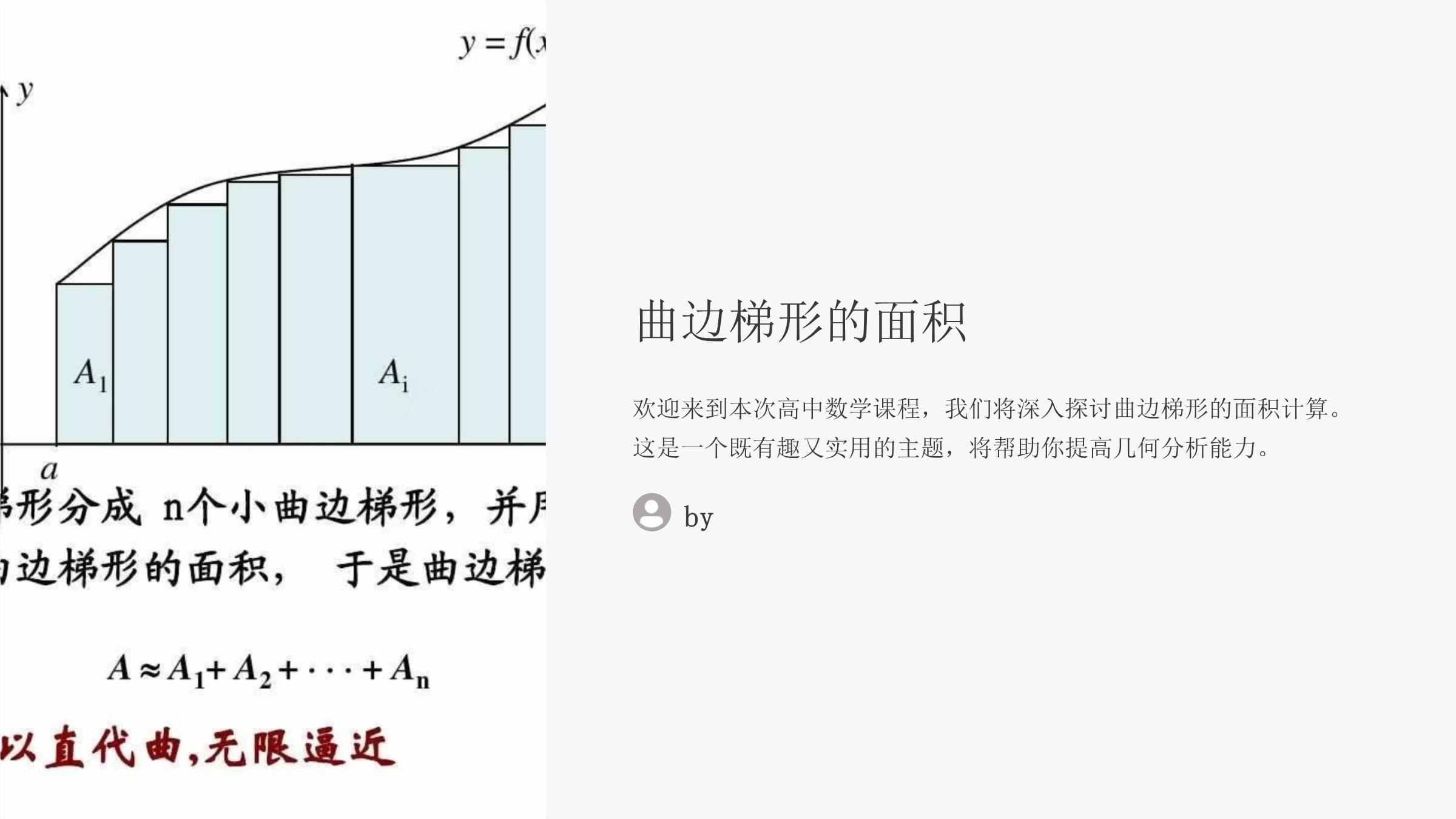
曲边梯形的面积欢迎来到本次高中数学课程，我们将深入探讨曲边梯形的面积计算。这是一个既有趣又实用的主题，将帮助你提高几何分析能力。by课程目标理解曲边梯形概念掌握曲边梯形的定义和特征。掌握计算方法学习并应用曲边梯形面积的计算公式。实际应用能力能够解决与曲边梯形相关的实际问题。数学思维提升培养几何直观和逻辑推理能力。什么是曲边梯形定义曲边梯形是一种特殊的几何图形，它由两条平行线段和两条曲线构成。这种图形在日常生活和工程设计中都有广泛应用。特点曲边梯形的独特之处在于它结合了直线和曲线元素，为面积计算带来了挑战和趣味。理解它的本质对于解决复杂几何问题至关重要。曲边梯形的特征平行边两条平行的直线段构成上下底。曲边两侧由曲线构成，可以是凸曲线或凹曲线。面积特性面积计算需要考虑曲线部分的影响。曲边梯形的分类凸曲边梯形两侧曲线向外凸出，形成凸形状。常见于建筑设计中的拱形结构。凹曲边梯形两侧曲线向内凹陷，形成凹形状。在某些机械零件设计中常见。混合曲边梯形一侧凸出，一侧凹陷。这种形状在自然界中较为常见，如某些叶片形状。曲边梯形的面积计算公式基本公式S=h(a+b)/2+S曲线部分曲线部分计算使用积分方法或近似法计算曲线与直线之间的面积。最终面积将梯形部分和曲线部分的面积相加得到总面积。举例说明1确定参数测量上下底长度和高度。2计算梯形部分使用梯形面积公式。3计算曲线部分应用积分或近似方法。4求和得出结果将两部分面积相加。案例分析1问题描述一个曲边梯形，上底3cm，下底7cm，高5cm，曲线部分面积为2cm²。求总面积。解题步骤计算梯形部分：S梯=5*(3+7)/2=25cm²加上曲线部分：S总=25+2=27cm²案例分析21识别图形2分解问题3应用公式4计算结果5验证答案通过这种系统的方法，我们可以解决更复杂的曲边梯形面积计算问题。案例分析3测量精确测量各个参数，包括曲线的弧度。计算运用适当的数学模型进行计算。验证使用不同方法交叉验证结果的准确性。曲边梯形面积计算步骤总结测量参数精确测量上下底长度和高度。计算梯形部分应用标准梯形面积公式。分析曲线部分选择合适方法计算曲线面积。合计总面积将所有计算结果相加。练习题1题目描述一个曲边梯形，上底4cm，下底8cm，高6cm，曲线部分面积为3cm²。求总面积。解题提示先计算梯形部分面积，再加上曲线部分面积。注意单位统一。答案总面积=6*(4+8)/2+3=39cm²练习题21题目分析仔细阅读题目，明确已知条件和求解目标。2数据整理列出所有已知参数，确保单位统一。3公式应用选择合适的公式，正确代入数据。4计算与检查仔细计算，并检查结果的合理性。练习题3实际问题一个花坛呈曲边梯形状，如何计算所需的草皮面积？上底5米，下底9米，高7米，曲线部分估算为4平方米。解决方案计算梯形部分：7*(5+9)/2=49平方米加上曲线部分：49+4=53平方米所需草皮面积约为53平方米。练习题4几何分析识别图形特征，确定关键参数。公式运用选择并正确应用相关公式。解题策略制定有效的解题步骤，逐步推进。结果验证检查计算过程，验证答案合理性。实际应用案例1建筑设计现代建筑中，曲边梯形常用于屋顶设计。精确计算面积对材料估算至关重要。计算方法结合CAD软件和数学模型，可以精确计算复杂曲面的面积。这对成本控制和施工规划都有重要意义。实际应用案例21航空工程飞机机翼截面常呈曲边梯形。精确计算对空气动力学性能至关重要。2计算方法使用高级数值模拟和积分技术，精确计算复杂曲面面积。3性能优化通过调整曲边梯形参数，可以优化升力和减小阻力。实际应用案例3地理测量在测量不规则地形时，常将其划分为多个曲边梯形。卫星技术利用卫星图像和GPS数据，精确测量大面积区域。面积计算结合传统测量和现代技术，提高计算精度。实际应用案例41识别问题在工程设计中发现需要计算曲边梯形面积的情况。2数据收集使用先进仪器精确测量所有必要参数。3模型建立根据实际情况建立合适的数学模型。4计算与验证运用计算机辅助设计软件进行计算并验证结果。学习小结1基础概念掌握2计算方法熟练3应用能力提升4问题解决技巧5实际运用insight通过本课程，我们系统地学习了曲边梯形的概念、特征、计算方法及其实际应用。这些知识将为今后的学习和工作奠定基础。掌握要点概念理解准确理解曲边梯形的定义和特征。计算技巧熟练运用面积计算公式，灵活处理各种情况。应用能力能够在实际问题中识别和应用曲边梯形知识。思维拓展培养数学思维，提高问题分析和解决能力。课后思考延伸思考曲边梯形的概念如何应用于其他几何图形的面积计算？创新应用在日常生活中，你能找到哪些曲边梯形的例子？如何计算它们的面积？跨学科联系曲边梯形的知识如何与物理、工程等学科结合？课后练习基础题计算给定参数的曲边梯形面积分析不同类型曲边梯形的特点进阶题解决复杂实际问题中的曲边梯形计算探讨曲边梯形在工程设计中的应用课堂互评小组讨论分组讨论课堂练习题，交流解题思路。解题展示选择代表上台展示解题过程，接受同学提问。互相评价同学间相互评价，提出改进建议。教学反馈1内容理解度评估学生对课程内容的掌握程度。2教学方法评价收集学生对教学方法的反馈意见。3难点分析识别学生学习过程中遇到的主要困难。4改进建议征集学生对课程改进的具体建议。教学评估85%掌握率学生对核心概念的平均掌握程度。92%参与度课堂讨论和练习的学生积极参与比例。78%应用能力学生能够解决实际问题的比例。拓展学习1在线资源推荐优质网络课程和学习资料。2课外读物推荐相关数学书籍，拓展知识面。3实践活动鼓励参与数学建模比赛，应用所学知识。4跨学科学习探索数学在其他学科中的应用。课程延伸物理学应用探讨曲边梯形在物理学中的应用，如流体力学。工程设计了解曲边梯形在建筑和机械