《导数和矢量运算》课件

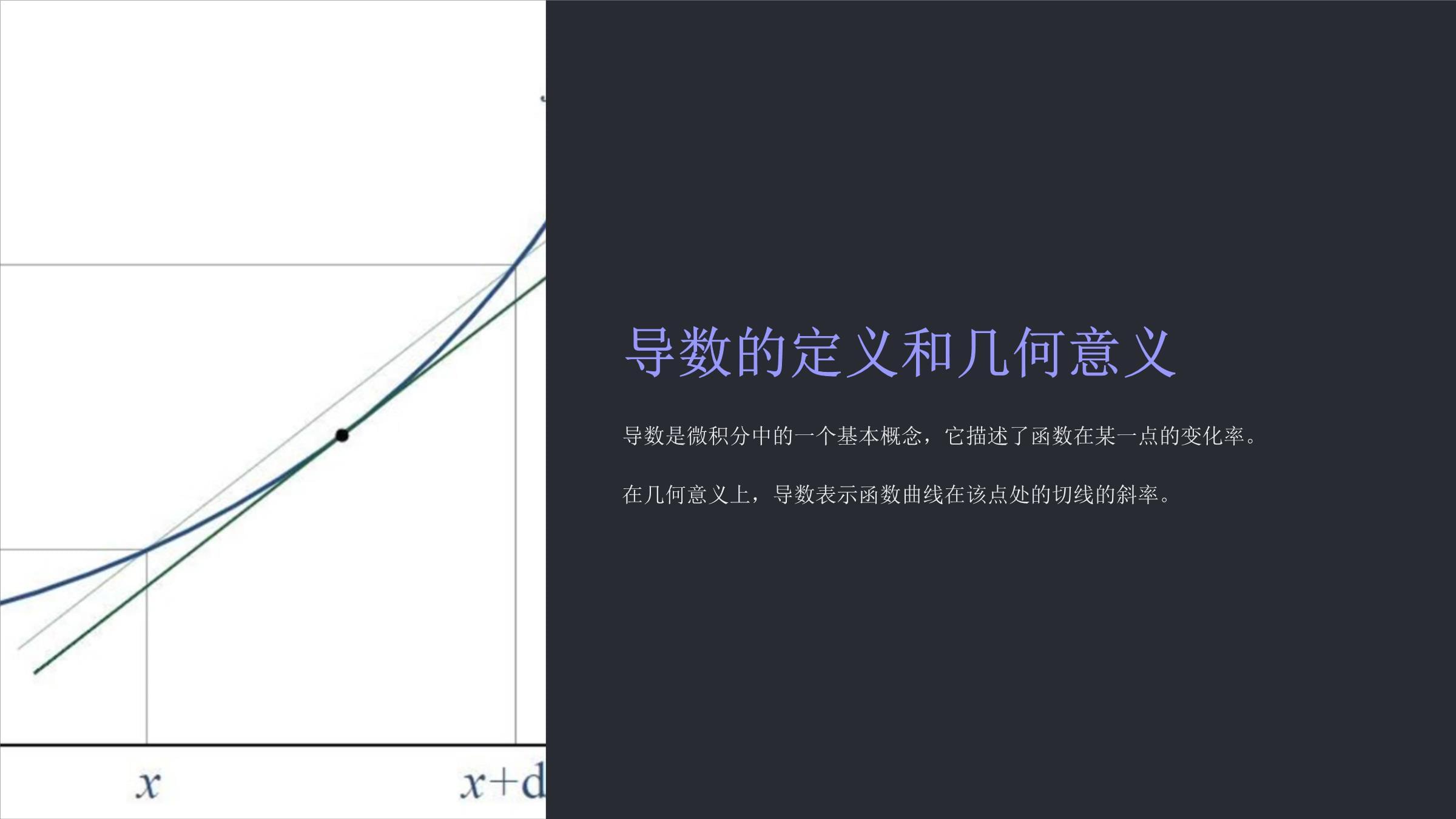
导数和矢量运算本课件介绍了微积分中导数的概念，并展示了矢量运算的应用。课程目标1理解导数的概念掌握导数的定义、几何意义和性质。2掌握导数的运算熟练运用求导公式和法则。3掌握矢量运算理解矢量的基本概念、运算规则和应用。4应用导数和矢量运算能够解决相关数学问题和实际问题。导数的定义和几何意义导数是微积分中的一个基本概念，它描述了函数在某一点的变化率。在几何意义上，导数表示函数曲线在该点处的切线的斜率。导数的性质线性性f(x)和g(x)可导，则f(x)+g(x)的导数为f'(x)+g'(x)。乘法法则f(x)和g(x)可导，则f(x)*g(x)的导数为f'(x)*g(x)+f(x)*g'(x)。除法法则f(x)和g(x)可导，且g(x)≠0，则f(x)/g(x)的导数为[f'(x)*g(x)-f(x)*g'(x)]/g(x)^2。链式法则f(x)和g(x)可导，则f(g(x))的导数为f'(g(x))*g'(x)。求导公式常数函数d/dx(c)=0幂函数d/dx(x^n)=nx^(n-1)指数函数d/dx(a^x)=a^x*ln(a)对数函数d/dx(log_a(x))=1/(x*ln(a))导数的应用1速度和加速度导数可以用来计算速度和加速度，可以用来分析物体的运动轨迹2优化问题导数可以用来寻找函数的最大值和最小值，可以用于解决许多优化问题3曲线拟合导数可以用来拟合曲线，可以用来预测未来的趋势一元函数的导数函数定义指一个变量对另一个变量的变化率。一个函数在一个点上的导数代表该函数在该点处的斜率。当函数自变量变化时，导数可以用来测量函数输出的变化量。极限概念导数的定义基于极限的概念。导数是函数在一个点上的瞬时变化率，它可以通过计算函数在该点附近两个点的斜率的极限来求得。求导公式导数的计算可以通过一些基本的求导公式和规则来完成。这些公式和规则可以用来求解各种函数的导数。隐函数的导数隐函数一个方程定义了一个函数，但无法直接将y表示为x的函数，称为隐函数。求导方法使用链式法则对隐函数方程两边求导，然后解出y'。应用在几何学中，隐函数常用于描述曲线，例如圆形，椭圆形，双曲线等。高阶导数定义高阶导数是指对函数进行多次求导得到的导数。一阶导数是函数本身的导数，二阶导数是一阶导数的导数，以此类推。应用高阶导数在许多领域都有应用，例如物理学中的运动学，工程学中的振动分析，以及经济学中的成本函数分析。矢量的基本概念矢量是具有大小和方向的物理量。它通常用箭头表示，箭头的长度代表矢量的大小，箭头指向的方向代表矢量的方向。矢量的数学表示通常用一个带箭头的字母，例如，矢量a。矢量在物理学、工程学和计算机图形学等领域中有着广泛的应用。矢量的代数运算1加法两个矢量的和为一个新的矢量，其起点与第一个矢量的起点相同，终点与第二个矢量的终点相同。2减法两个矢量的差为一个新的矢量，其起点与第一个矢量的起点相同，终点与第二个矢量的终点相同，但方向相反。3数乘一个矢量与一个标量的乘积为一个新的矢量，其方向与原矢量相同，长度为原矢量长度的标量倍数。矢量的标量积定义两个矢量的标量积是一个标量，等于这两个矢量的模长乘以它们夹角的余弦。性质标量积满足交换律和分配律。几何意义标量积可以表示两个矢量之间的投影关系。矢量的矢量积定义两个矢量的矢量积是一个新的矢量，其大小等于这两个矢量大小的乘积再乘以它们夹角的正弦值，其方向垂直于这两个矢量所在的平面，并遵循右手螺旋定则。性质不满足交换律：a×b≠b×a满足分配律：a×(b+c)=a×b+a×c与标量相乘：(ka)×b=a×(kb)=k(a×b)应用矢量积在物理学中有着广泛的应用，例如计算力矩、磁场力等。矢量的混合积混合积是三个矢量进行的运算，结果是一个标量。混合积的绝对值等于以三个矢量为棱的平行六面体的体积。混合积的符号取决于三个矢量的相对方向。矢量微分运算梯度表示一个标量场在空间中的变化率，它指向变化率最大的方向。散度衡量矢量场在一点上的发散程度，它表示矢量场在该点上的源或汇的强度。旋度表示矢量场在空间中的旋转程度，它指向旋转轴的方向，大小表示旋转的强度。拉普拉斯算子是一个二阶微分算子，它将一个标量场或矢量场映射到另一个标量场或矢量场。梯度定义梯度是多元函数在某一点方向导数中取最大值的方向。方向导数方向导数表示函数在某一点沿某一方向的变化率。梯度的意义梯度方向是函数在该点上升最快的方向。散度矢量场散度表示矢量场在某一点的扩张程度，即矢量场在该点汇聚或发散的趋势。流动散度可以理解为流体的“源”或“汇”，正值表示该点是流体的源，负值表示该点是流体的汇。计算散度可以用偏导数来计算，表示矢量场各分量在对应坐标方向上的变化率。旋度定义旋度是一个向量，表示一个向量场的旋转程度。计算旋度的计算方法是通过向量场的偏导数。应用旋度在流体力学、电磁学等领域有广泛应用，例如计算流体的涡量。拉普拉斯算子定义拉普拉斯算子是一个二阶微分算子，它是一个矢量微分算子，是梯度算子的散度。它是描述一个函数在多元空间中是否为调和函数的工具。应用拉普拉斯算子在许多物理学领域都有应用，例如热传导、电磁学、流体力学等。矢量微分的应用1物理学电磁场、流体力学2工程学热传导、应力分析3计算机图形学光线追踪、纹理映射线积分定义线积分是对一个标量函数或矢量函数在曲线上的积分。应用线积分在物理学中有很多应用，例如计算功、力矩、磁通量等。曲面积分定义曲面积分是指对曲面上的函数值进行积分，用来计算曲面上的量，例如曲面的面积、曲面的质量等。类型第一类曲面积分第二类曲面积分应用在物理学、工程学、数学等领域都有广泛的应用，例如计算流体的流量、计算电磁场的强度等。格林公式定义格林公式将平面区域上的曲线积分与该区域上的二重积分联系起来。应用格林公式可用于计算平面区域的面积、曲线积分的计算以及其他相关问题。推导格林公式可通过斯托克斯定理推导得到，它是向量微积分中的重要定理。散度定理体积散度定理将一个向量场穿过一个封闭曲面的通量与该向量场在封闭曲面所包围的体积内的散度的积分联系起来。通量通量是指一个向量场穿过一个曲面的数量，它反映了向量场在该曲面上的流动强度。积分散度定理将一个向量场穿过一个封闭曲面的通量表示为该向量场在封闭曲面所包围的体积内的散度的积分。斯托克斯公式1积分将一个曲线积分转化为一个曲面积分。2向量场在满足一定条件的向量场中，线积分与曲面积分之间建立了联系。3应用广泛用于物理学，例如计算流体动力学、电磁场等。综合应用导数和矢量运算在各个领域都有广泛的应用。例如，在物理学中，导数可以用来描述运动和力，矢量运算可以用来描述力、速度、加速度等物理量。在工程学中，导数和矢量运算可以用来分析结构力学、流体力学、热力学等问题。在经济学中，导数和矢量运算可以用来研究市场需求、成本和利润等经济问题。课程小结导数导数的概念、性质和应用。矢量运算矢量的基本概念、代数运算和微分运算。矢量积分线积分、曲面积分和格林公式、散度定理、斯托克斯公式。思考与讨论本课程介绍了导