2025年人教新起点高一数学上册月考试卷

…………○…………内…………○…………装…………○…………内…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………外…………○…………装…………○…………订…………○…………线…………○…………第=page22页，总=sectionpages22页第=page11页，总=sectionpages11页2025年人教新起点高一数学上册月考试卷310考试试卷考试范围：全部知识点；考试时间：120分钟学校：______姓名：______班级：______考号：______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共6题，共12分)1、若P（A∪B）=P（A）+P（B）=1；则事件A与B的关系是（）

A.互斥不对立。

B.对立不互斥。

C.互斥且对立。

D.以上都不对。

2、【题文】已知则是成立的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件3、【题文】下列各组函数中；表示同一函数的是（）

⑴

⑵

⑶，；

⑷，；

⑸A.⑴、⑵B.⑵、⑶C.⑷D.⑶、⑸4、【题文】如果那么等于（）

5、下列不等式中正确的是(

)

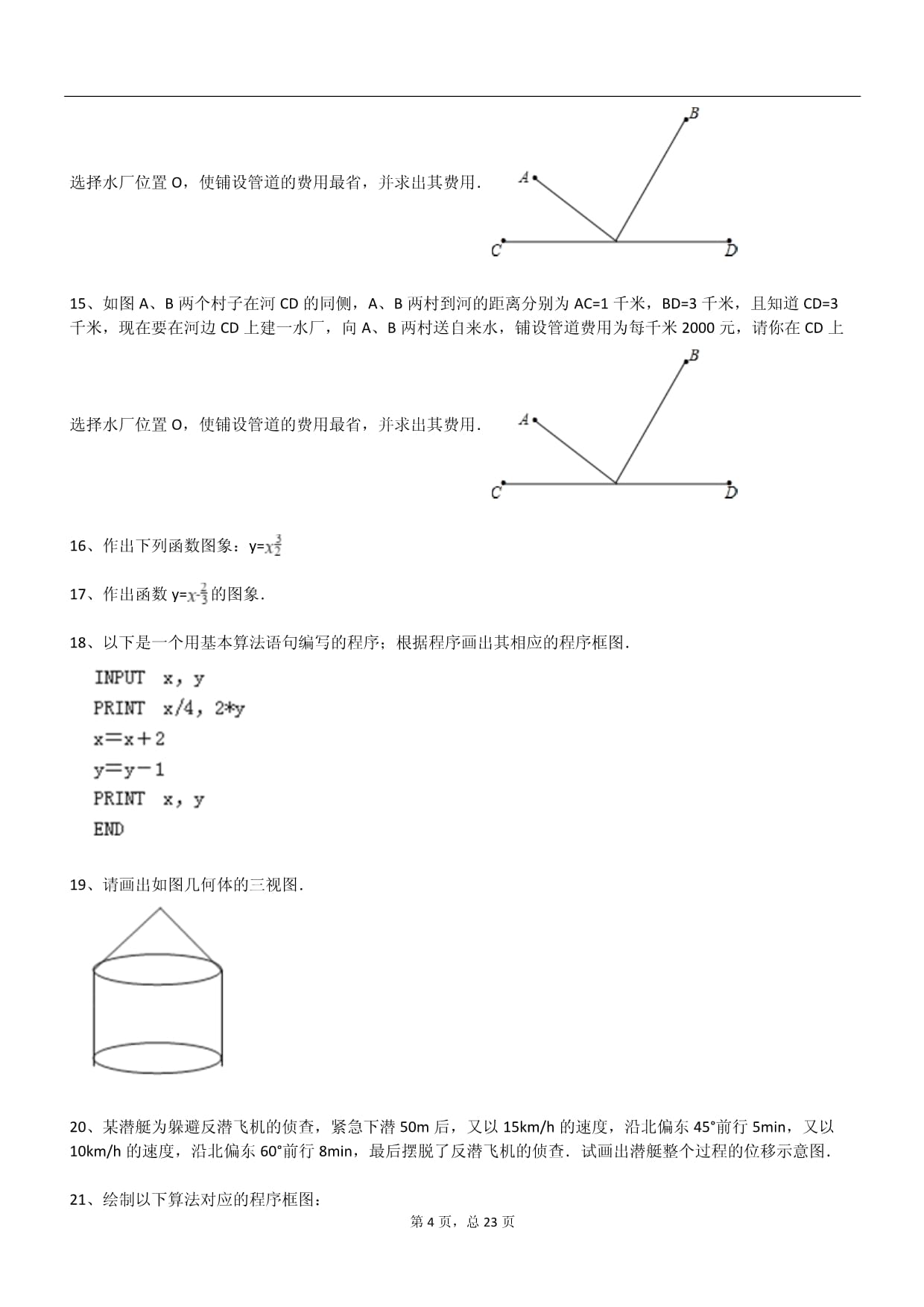
A.sin57娄脨>sin47娄脨

B.tan158娄脨>tan(鈭�娄脨7)

C.sin(鈭�娄脨5)>sin(鈭�娄脨6)

D.cos(鈭�35娄脨)>cos(鈭�94娄脨)

6、方程log5x+x鈭�2=0

的根所在的区间是(

)

A.(2,3)

B.(1,2)

C.(3,4)

D.(0,1)

评卷人得分二、填空题(共7题，共14分)7、函数x∈R的部分图象如右图所示．设P是图象上的最高点，M，N是图象与x轴的交点，则tan∠MPN=____．

8、函数且在上的最大值与最小值的差为则____。9、两平行直线间的距离为____10、设函数则的值为．11、【题文】已知圆锥的底面半径为2cm，高为1cm，则圆锥的侧面积是____cm2．12、【题文】已知幂函数f（x）图象过点（8，4），则f（x）的值域为____。13、方程log5（2x+1）=log5（x2-2）的解是______．评卷人得分三、作图题(共9题，共18分)14、如图A、B两个村子在河CD的同侧，A、B两村到河的距离分别为AC=1千米，BD=3千米，且知道CD=3千米，现在要在河边CD上建一水厂，向A、B两村送自来水，铺设管道费用为每千米2000元，请你在CD上选择水厂位置O，使铺设管道的费用最省，并求出其费用．15、如图A、B两个村子在河CD的同侧，A、B两村到河的距离分别为AC=1千米，BD=3千米，且知道CD=3千米，现在要在河边CD上建一水厂，向A、B两村送自来水，铺设管道费用为每千米2000元，请你在CD上选择水厂位置O，使铺设管道的费用最省，并求出其费用．16、作出下列函数图象：y=17、作出函数y=的图象．18、以下是一个用基本算法语句编写的程序；根据程序画出其相应的程序框图．

19、请画出如图几何体的三视图．

20、某潜艇为躲避反潜飞机的侦查，紧急下潜50m后，又以15km/h的速度，沿北偏东45°前行5min，又以10km/h的速度，沿北偏东60°前行8min，最后摆脱了反潜飞机的侦查．试画出潜艇整个过程的位移示意图．21、绘制以下算法对应的程序框图：

第一步；输入变量x；

第二步，根据函数f（x）=

对变量y赋值；使y=f（x）；

第三步，输出变量y的值．22、已知简单组合体如图；试画出它的三视图（尺寸不做严格要求）

评卷人得分四、解答题(共3题，共27分)23、设A={x|x2-ax+a2-19=0}，B={x|x2-5x+6=0}，C={x|x2+2x-8=0}．求分别满足下列条件的a的值．

（1）A∩B=A∪B；

（2）A∩B≠φ；且A∩C=φ．

24、【题文】如图，四棱锥的底面是边长为2的菱形，已知

（Ⅰ）证明：

（Ⅱ）若为的中点，求三菱锥的体积.25、已知函数f(x)=log2x

(1)

解关于x

的不等式f(x+1)鈭�f(x)>1

(2)

设函数g(x)=f(2x+1)+kx

若g(x)

的图象关于y

轴对称，求实数k

的值．评卷人得分五、计算题(共1题，共9分)26、若⊙O和⊙O′相外切，它们的半径分别为8和3，则圆心距OO′为____．评卷人得分六、综合题(共1题，共2分)27、如图，已知：⊙O1与⊙O2外切于点O，以直线O1O2为x轴，点O为坐标原点，建立直角坐标系，直线AB切⊙O1于点B，切⊙O2于点A，交y轴于点C（0，2），交x轴于点M．BO的延长线交⊙O2于点D；且OB：OD=1：3．

（1）求⊙O2半径的长；

（2）求线段AB的解析式；

（3）在直线AB上是否存在点P，使△MO2P与△MOB相似？若存在，求出点P的坐标与此时k=的值，若不存在，说明理由．参考答案一、选择题(共6题，共12分)1、D【分析】

设掷一枚硬币3次；事件A：“至少出现一次正面”，事件B：“3次出现正面”；

则P（A）=P（B）=

满足P（A）+P（B）=1；

但A；B不是互斥事件也不是对立事件。

故选D．

【解析】【答案】通过举例子；得到满足P（A∪B）=P（A）+P（B）=1的两个事件不一定互斥也不一定对立．

2、A【分析】【解析】

试题分析：p:-5≤x≤3；q：2＜x＜3；P不能推得q，q可以推得p，所以答案是A.

考点：充要条件的判断.【解析】【答案】A3、C【分析】【解析】略【解析】【答案】C4、D【分析】【解析】

由题干可得：故选【解析】【答案】

D5、B【分析】解：对于选项A：sin5娄脨7=sin(娄脨鈭�2娄脨7)=sin2娄脨7

sin4娄脨7=sin(娄脨鈭�3娄脨7)=sin3娄脨7

隆脽0<2娄脨7<3娄脨7<娄脨2

隆脿sin2娄脨7<sin3娄脨7

隆脿

选项A错误；

对于选项B：

tan15娄脨8=tan(2娄脨鈭�娄脨8)=鈭�tan娄脨8

隆脽tan(鈭�娄脨7)=鈭�tan娄脨7

隆脽娄脨8<娄脨7

隆脿tan娄脨8<tan娄脨7

隆脿鈭�tan娄脨8>鈭�tan娄脨7

隆脿

选项B正确；

对于选项C：

sin(鈭�娄脨5)=鈭�sin娄脨5<sin(鈭�娄脨6)=鈭�sin娄脨6

隆脿

选项C错误；

对于选项D：

cos(鈭�3娄脨5)=cos3娄脨5=cos(娄脨鈭�2娄脨5)=鈭�cos2娄脨5<0

cos(鈭�9娄脨4)=cos9娄脨4=cos(2娄脨+娄脨4)=cos娄脨4>0

隆脿

选项D错误；

综上；只有选项B正确；

故选：B

．

结合诱导公式和三角函数的单调性；对选项进行逐一排除即可得到相应的答案．

本题重点考查了诱导公式及其应用、三角函数的单调性与比较大小问题处理方法，属于中档题．【解析】B

6、B【分析】解：方程log5x+x鈭�2=0

的根就是y=log5x+x鈭�2

的零点；

函数是连续函数；是增函数；

可得f(1)=0+1鈭�2=鈭�1<0f(2)=log52+2鈭�2>0

所以f(1)f(2)<0

方程根在(1,2)

．

故选：B

．

方程的根转化为函数的零点；判断函数的连续性以及单调性，然后利用零点判定定理推出结果即可．

本题考查函数的零点判定定理的应用，考查计算能力．【解析】B

二、填空题(共7题，共14分)7、略

【分析】

函数x∈R的部分图象如右图所示．设P是图象上的最高点，M，N是图象与x轴的交点；

所以MN==1，P到MN的距离为：1，所以tan∠MPN==．

故答案为：．

【解析】【答案】由题意求出函数的周期；推出MN的长度，得到P到MN的距离，然后求出tan∠MPN即可．

8、略

【分析】当a>1时，函数为单调增函数，上的最大值与最小值的差为解得a=当0<1时，函数为单调减函数，上的最大值与最小值的差为解得a=综上所述或【解析】【答案】或9、略

【分析】【解析】【答案】110、略

【分析】试题分析：考点：根据函数解析式求函数的值【解析】【答案】411、略

【分析】【解析】

试题分析：圆锥的底面周长为：母线长为：故答案为

考点：圆锥侧面积的求法.【解析】【答案】12、略

【分析】【解析】略【解析】【答案】13、略

【分析】解：∵log5（2x+1）=log5（x2-2）；

∴

解得x=3．

故答案为：x=3．

根据对数函数的性质知log5（2x+1）=log5（x2-2）等价于由此能求出其解集．

本题考查对数方程的解法，解题时要认真审题，注意对数函数的图象和性质的灵活运用．【解析】x=3三、作图题(共9题，共18分)14、略

【分析】【分析】作点A关于河CD的对称点A′，当水厂位置O在线段AA′上时，铺设管道的费用最省．【解析】【解答】解：作点A关于河CD的对称点A′；连接A′B，交CD与点O，则点O即为水厂位置，此时铺设的管道长度为OA+OB．

∵点A与点A′关于CD对称；

∴OA′=OA；A′C=AC=1；

∴OA+OB=OA′+OB=A′B．

过点A′作A′E⊥BE于E；则∠A′EB=90°，A′E=CD=3，BE=BD+DE=3+1=4；

∴在Rt△A′BE中，A′B==5（千米）；

∴2000×5=10000（元）．

答：铺设管道的最省费用为10000元．15、略

【分析】【分析】作点A关于河CD的对称点A′，当水厂位置O在线段AA′上时，铺设管道的费用最省．【解析】【解答】解：作点A关于河CD的对称点A′；连接A′B，交CD与点O，则点O即为水厂位置，此时铺设的管道长度为OA+OB．

∵点A与点A′关于CD对称；

∴OA′=OA；A′C=AC=1；

∴OA+OB=OA′+OB=A′B．

过点A′作A′E⊥BE于E；则∠A′EB=90°，A′E=CD=3，BE=BD+DE=3+1=4；

∴在Rt△A′BE中，A′B==5（千米）；

∴2000×5=10000（元）．

答：铺设管道的最省费用为10000元．16、【解答】幂函数y={#mathml#}x32

{#/mathml#}的定义域是[0；+∞），图象在第一象限，过原点且单调递增，如图所示；

【分析】【分析】根据幂函数的图象与性质，分别画出题目中的函数图象即可．17、【解答】图象如图所示。

【分析】【分析】描点画图即可18、解：程序框图如下：

【分析】【分析】根据题目中的程序语言，得出该程序是顺序结构，利用构成程序框的图形符号及其作用，即可画出流程图．19、解：如图所示：

【分析】【分析】由几何体是圆柱上面放一个圆锥，从正面，左面，上面看几何体分别得到的图形分别是长方形上边加一个三角形，长方形上边加一个三角形，圆加一点．20、解：由题意作示意图如下；

【分析】【分析】由题意作示意图。21、解：程序框图如下：

【分析】【分析】该函数是分段函数，当x取不同范围内的值时，函数解析式不同，因此当给出一个自变量x的值时，必须先判断x的范围，然后确定利用哪一段的解析式求函数值，因为函数解析式分了三段，所以判断框需要两个，即进行两次判断，于是，即可画出相应的程序框图．22、

解：几何体的三视图为：

【分析】【分析】利用三视图的作法，画出三视图即可．四、解答题(共3题，共27分)23、略

【分析】

（1）B={x|x2-5x+6=0}={2，3}，C={x|x2+2x-8=0}={2；-4}．

∵A∩B=A∪B；

∴A=B={2；3}；

说明方程x2-ax+a2-19=0的两个根为：2；3．

∴a=5．

（2）∵A∩B≠φ；且A∩C=φ；

即说明集合A；B有相同元素，A，C没有相同元素；

∴2∉A；且3∈A；

说明方程x2-ax+a2-19=0的一个根为：3；

∴x2-ax+a2-19=0⇒a=-2或a=5

若a=-2；则A={-5，3}，符合题意；

若a=5；则A={2，3}，不合，舍去．

∴a=-2．

【解析】【答案】（1）利用一元二次方程化简集合B，C，结合A∩B=A∪B，得出A=B={2，3}，说明方程x2-ax+a2-19=0的两个根为：2；3．从而求出a值；

（2）利用题中条件：A∩B≠φ，且A∩C=φ得出3∈A，说明方程x2-ax+a2-19=0的一个根为：3；从而求出a值．

24、略

【分析】【解析】

（1）证明：连接交于点。

又是菱形

而⊥面⊥

(2)由（1）⊥面

=

（1）证明线线垂直，需要线面垂直证起；（2）的面积是的面积的2倍，是点到面的高；求出面积和高，即能求出最终的体积.

【考点定位】考查空间直线与直线，直线与平面的位置，.三棱锥体积等基础知识和基本技能，考查空间观念，推理论证能力和运算能力.【解析】【答案】（Ⅰ）见解析（Ⅱ）25、略

【分析】

(1)

根据对数的运算性质得到关于x

的不等式；解出即可；

(2)

求出g(x)

的解析式；根据对数的运算得到关于k

的方程，求出k

的值即可．

本题考查了对数的运算性质以及对数函数的性质，考查转化思想，是一道中档题．【解析】解：(1)

因为f(x+1)鈭�f(x)>1

所以2(x+1)鈭�log2x>1

即：log2x+1x>1

所以x+1x>2

由题意，x>0

解得0<x<1

所以解集为{x|0<x<1}.(5

分)

(2)g(x)=f(2x+1)+kx=2(2x+1)+kx

由题意；g(x)

是偶函数；

所以?x隆脢R

有f(鈭�x)=f(x)

即：2(2鈭�x+1)鈭�kx=2(2x+1)+kx

成立；

所以2(2鈭�x+1)鈭�2(2x+1)=2kx

即：log22鈭�x+12x+1=2kx

所以log22鈭�x=2kx

所以鈭�x=2kx(2k+1)x=0

所以k=鈭�12.(12

分)

五、计算题(共1题，共9分)26、略

【分析】【分析】由两圆的半径分别为8和3，这两个圆外切，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可求得它们的圆心距．【解析】【解答】解：∵两圆的半径分别为3和8；这两个圆外切；

∴3+8=11；

∴它们的圆心距等于11．

故答案为：11．六、综合题(共1题，共2分)27、略

【分析】【分析】（1）连接BO1，DO2，O2A作O1N⊥O2A于N，连接OA，根据切线长定理求出AB的长，设O1B为r，根据勾股定理得到方程（4r）2-（2r）2=42；求出方程的解即可；

（2）求出∠CMO=∠NO1O2=30°，求出OM，设AB的解析式是y=kx+b；把C；M的坐标代入得到方程组，求出方程组的解即可；

（3）①∠MO2P=30°，过B作BQ⊥OM于Q，求出MQ，BQ，过P'作P'W⊥X轴于W，根据相似三角形的性质求出PW即可得到P的坐标，根据相似三角形的性质求出k即可；②∠MO2P=120°，过P作PZ⊥X轴于Z，根据含30度角的直角三角形性质求出PZ，即可得到P的坐标，根据相似三角形的性质求出k即可．【解析】【解答】解：（1）连接BO1，O2