



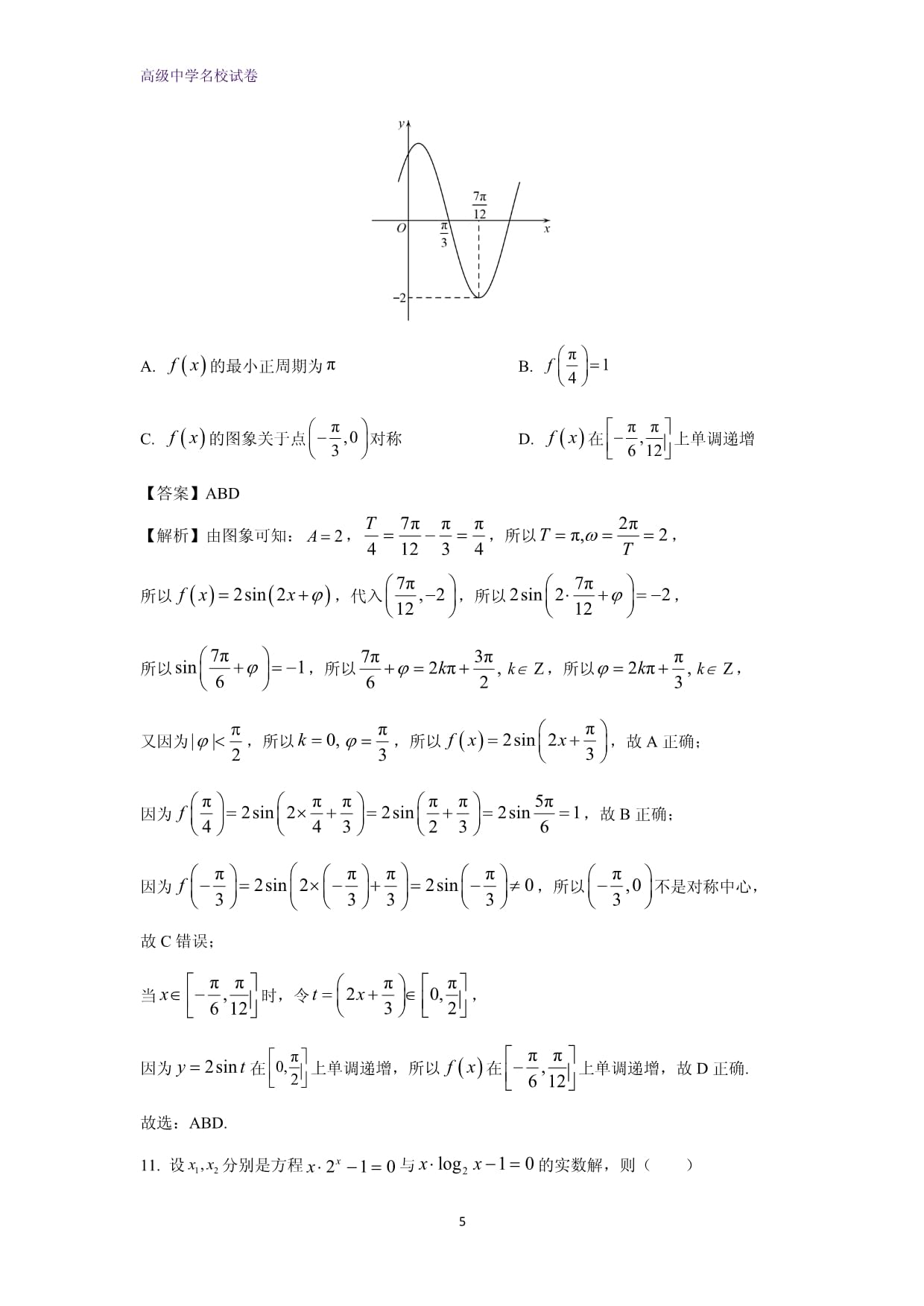
版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
高级中学名校试卷PAGEPAGE1山西省晋中市2023-2024学年高一上学期期末调研数学试题一、单项选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题“∃x>0,x2>2x的否定是()A.∃x0,x2>2x B.∀x0,x22xC.∀x>0,x22x D.∃x>0,x2<2x【答案】C【解析】变为,的否定为,所以原命题的否定为“,”.故选:C2.已知集合,,,则()A. B. C. D.【答案】C【解析】因为,所以,对于A选项,因为,故A选项错误;对于B选项,因为,故B选项错误;对于C选项,因为,故C选项正确;对于D选项,,故D选项错误.故选:C.3.已知,则()A. B. C. D.【答案】A【解析】.故选:A.4.下列函数是偶函数且在上单调递减的是()A. B. C. D.【答案】D【解析】对于A,,为奇函数,选项A错误;对于B,,为奇函数,选项B错误;对于C,,即函数不单调,选项C错误;对于B,,,故为偶函数,又函数在上单调递减,选项D正确.故选:D.5.已知,,则“”是“”的()A.充要条件 B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件【答案】C【解析】,,,,,即成立,反之,,若,则不成立,所以“”是“”成立的必要不充分条件.故选:C.6.已知,,,则()A. B. C. D.【答案】C【解析】由指数函数单调性可知:,由对数函数单调性可知:,由上可知:.故选:C.7.已知函数的图象如图所示,则的解析式可以是()A. B.C. D.【答案】A【解析】对于B,,当趋于正无穷时,是一个负数,即为负数,排除B选项;因为和的定义域都为不满足所给图象,排除C、D选项.故选:A.8.已知点,分别以,为起点同时出发,沿单位圆(为坐标原点)逆时针做匀速圆周运动,若点的角速度为,点的角速度为,则,第二次重合时的坐标为()A. B.C. D.【答案】B【解析】设运动时间为,则点坐标为,点坐标为,则,第二次重合时,,此时点坐标为:即.故选:B.二、多项选择题:本题共4小题,在每小题给出的四个选项中,有多项符合题目要求.9.已知,,则()A. B. C. D.【答案】BC【解析】对于A:取,此时,即,故A错误;对于B:因为,所以,又因为,所以成立,故B正确;对于C:因为,所以,又因为,所以,所以,又因为,且,,所以,故C正确;对于D:取,此时,显然不成立,故D错误.故选:BC.10.已知函数(,,)部分图象如图所示,则()A.的最小正周期为 B.C.的图象关于点对称 D.在上单调递增【答案】ABD【解析】由图象可知:,,所以,所以,代入,所以,所以,所以,所以,又因为,所以,所以,故A正确;因为,故B正确;因为,所以不是对称中心,故C错误;当时,令,因为在上单调递增,所以在上单调递增,故D正确.故选:ABD.11.设分别是方程与的实数解,则()A. B. C. D.【答案】ACD【解析】方程与分别变形为:,因为和互为反函数,且关于对称,所以,故CD正确;画出和,的图象,易知A正确;又因为,结合图象,易知,故B错误.故选:ACD.12.已知,,均为不等于零的实数,且满足,则下列说法正确的是()A. B.当时,的最大值为1C.当时,的最大值为1 D.当时,的最大值为1【答案】BD【解析】对于选项A,当,因为,可得,但是此时,故选项A错误;对于选项B,因为,,,所以,故,所以,且,所以的最大值为1,故选项B正确;对于选项C,当时,因为,所以可求,所以的最大值不为1,故选项C错误;对于选项D,因为,,所以,所以,因为,所以时取等号,所以,且,所以的最大值为1,故选项D正确.故选:BD.三、填空题:本题共4小题.13.已知函数若,则_________.【答案】2【解析】因为所以,解得.故答案为:2.14.已知扇形的周长为10,面积为6,则这个扇形的圆心角(正角)的弧度数为_________.【答案】或【解析】如图所示,设扇形的半径为,弧长为,由题意可得,解得,或,当,时,扇形的圆心角为;当,时,扇形的圆心角为;所以该扇形的圆心角为或.故答案为:或.15.为了践行“绿水青山就是金山银山”的生态环保理念,某地计划改善生态环境,大力开展植树造林活动.该地计划每年都植树造林,若森林面积的年增长率相同,则需要5年时间使森林面积变为原来的2倍,为使森林面积变为原来的5倍以上,至少需要植树造林______年.(结果精确到整数,参考数据:)【答案】12【解析】设森林面积为m,森林面积的年增长率为,则5年时间森林面积变为,则,若需要植树造林x年,使得森林面积变为原来的5倍以上,则有,即,则有,所以为使森林面积变为原来的5倍以上,至少需要植树造林12年.故答案为:12.16.已知函数在区间内恰有一个零点,则实数的取值范围是__________________.【答案】【解析】当时,,令得,符合题意;当时,是二次函数,对于方程,只需,即,解得,且,当时,,此时,得或,符合题意,当时,,此时,得或,符合题意,综上,实数的取值范围为.故答案为:.四、解答题:解答应写出文字说明、证明过程或演算步骤.17.已知不等式的解集为.(1)求不等式的解集;(2)设非空集合,若是的充分不必要条件,求的取值范围.解:(1)因为不等式的解集为,所以方程的解为,所以,,得,,则不等式即,解得,故解集.(2)由(1)知,,而是的充分不必要条件,则是的真子集,所以,解得,综上所述,的取值范围是.18.已知,,且,.(1)求,;(2)求.解:(1)由题意知,,因为,所以,所以,所以.(2)由,,可得,,所以,,因为,所以.19.已知函数是奇函数.(1)求实数的值;(2)求关于的不等式的解集.解:(1)因为是奇函数,所以对定义域内的任意恒成立,则对任意定义域内的任意恒成立,所以,,当时,定义域为,不关于原点对称,舍去,当时,,符合条件,所以.(2),的定义域为,当时,,解得,当时,,解得,综上,当时,原不等式的解集为;当时,原不等式的解集为.20.某工厂生产某种产品,受生产能力、技术水平以及机器设备老化等问题的影响,每天都会生产出一些次品,根据对以往产品中次品的分析,得出每日次品数(万件)与日产量(万件)之间满足关系式(其中为小于6的正常数).对以往的销售和利润情况进行分析,知道每生产1万件合格品可以盈利4万元,但每生产1万件次品将亏损2万元,该工厂需要作决策定出合适的日产量.(1)求每天的利润(万元)与的函数关系式;(2)分别在和的条件下计算当日产量为多少万件时可获得最大利润.解:(1)由题意得:当时,,当时,,综上,.(2)令,则,若,当时,每天的利润为0,当时,,在上单调递减,故最大值在即时取到,为;若,当,每天的利润为0,当时,,,当且仅当时等号成立,故最大值在,即时取到,为,综上,若,则当日产量为2万件时,可获得最大利润;若,则当日产量为3万件时,可获得最大利润.21.已知函数,,满足,.(1)求的解析式;(2)将的图象上各点的横坐标伸长为原来的4倍(纵坐标不变),再将得到的图象向左平移个单位长度,得到函数的图象,求在上的值域.解:(1),由题意可知:在处取到最大值,则,解得,又因为,故只有时成立,得,所以.(2)将的图象上各点的横坐标伸长为原来的4倍,得到的图象,再将得到的图象向左平移个单位长度,得的图象,令,当时,,在上单调递增,在上单调递减,故,所以,当时,,当时,,故在上的值域为.22.已知函数的定义域为,且,,都有成立.(1)求,的值,并判断的奇偶性.(2)已知函数,当时,.(i)判断在上的单调性;(ii)若均有,求满足条件的最小的正整数.解:(1)令,得,解得,令,得,故,令,得,即,又的定义域为,关于原点对称,所以是奇函数.(2)(i)由,可得,即,,且,有,因为,所以,从而,得,因此在上单调递减.(ii)因为,,所以是偶函数,,而在上单调递减,则有或,由题可知,只需考虑成立,从而有,因为,所以,则的最大值在处取到,故只需,综上,满足条件的最小的正整数.山西省晋中市2023-2024学年高一上学期期末调研数学试题一、单项选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题“∃x>0,x2>2x的否定是()A.∃x0,x2>2x B.∀x0,x22xC.∀x>0,x22x D.∃x>0,x2<2x【答案】C【解析】变为,的否定为,所以原命题的否定为“,”.故选:C2.已知集合,,,则()A. B. C. D.【答案】C【解析】因为,所以,对于A选项,因为,故A选项错误;对于B选项,因为,故B选项错误;对于C选项,因为,故C选项正确;对于D选项,,故D选项错误.故选:C.3.已知,则()A. B. C. D.【答案】A【解析】.故选:A.4.下列函数是偶函数且在上单调递减的是()A. B. C. D.【答案】D【解析】对于A,,为奇函数,选项A错误;对于B,,为奇函数,选项B错误;对于C,,即函数不单调,选项C错误;对于B,,,故为偶函数,又函数在上单调递减,选项D正确.故选:D.5.已知,,则“”是“”的()A.充要条件 B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件【答案】C【解析】,,,,,即成立,反之,,若,则不成立,所以“”是“”成立的必要不充分条件.故选:C.6.已知,,,则()A. B. C. D.【答案】C【解析】由指数函数单调性可知:,由对数函数单调性可知:,由上可知:.故选:C.7.已知函数的图象如图所示,则的解析式可以是()A. B.C. D.【答案】A【解析】对于B,,当趋于正无穷时,是一个负数,即为负数,排除B选项;因为和的定义域都为不满足所给图象,排除C、D选项.故选:A.8.已知点,分别以,为起点同时出发,沿单位圆(为坐标原点)逆时针做匀速圆周运动,若点的角速度为,点的角速度为,则,第二次重合时的坐标为()A. B.C. D.【答案】B【解析】设运动时间为,则点坐标为,点坐标为,则,第二次重合时,,此时点坐标为:即.故选:B.二、多项选择题:本题共4小题,在每小题给出的四个选项中,有多项符合题目要求.9.已知,,则()A. B. C. D.【答案】BC【解析】对于A:取,此时,即,故A错误;对于B:因为,所以,又因为,所以成立,故B正确;对于C:因为,所以,又因为,所以,所以,又因为,且,,所以,故C正确;对于D:取,此时,显然不成立,故D错误.故选:BC.10.已知函数(,,)部分图象如图所示,则()A.的最小正周期为 B.C.的图象关于点对称 D.在上单调递增【答案】ABD【解析】由图象可知:,,所以,所以,代入,所以,所以,所以,所以,又因为,所以,所以,故A正确;因为,故B正确;因为,所以不是对称中心,故C错误;当时,令,因为在上单调递增,所以在上单调递增,故D正确.故选:ABD.11.设分别是方程与的实数解,则()A. B. C. D.【答案】ACD【解析】方程与分别变形为:,因为和互为反函数,且关于对称,所以,故CD正确;画出和,的图象,易知A正确;又因为,结合图象,易知,故B错误.故选:ACD.12.已知,,均为不等于零的实数,且满足,则下列说法正确的是()A. B.当时,的最大值为1C.当时,的最大值为1 D.当时,的最大值为1【答案】BD【解析】对于选项A,当,因为,可得,但是此时,故选项A错误;对于选项B,因为,,,所以,故,所以,且,所以的最大值为1,故选项B正确;对于选项C,当时,因为,所以可求,所以的最大值不为1,故选项C错误;对于选项D,因为,,所以,所以,因为,所以时取等号,所以,且,所以的最大值为1,故选项D正确.故选:BD.三、填空题:本题共4小题.13.已知函数若,则_________.【答案】2【解析】因为所以,解得.故答案为:2.14.已知扇形的周长为10,面积为6,则这个扇形的圆心角(正角)的弧度数为_________.【答案】或【解析】如图所示,设扇形的半径为,弧长为,由题意可得,解得,或,当,时,扇形的圆心角为;当,时,扇形的圆心角为;所以该扇形的圆心角为或.故答案为:或.15.为了践行“绿水青山就是金山银山”的生态环保理念,某地计划改善生态环境,大力开展植树造林活动.该地计划每年都植树造林,若森林面积的年增长率相同,则需要5年时间使森林面积变为原来的2倍,为使森林面积变为原来的5倍以上,至少需要植树造林______年.(结果精确到整数,参考数据:)【答案】12【解析】设森林面积为m,森林面积的年增长率为,则5年时间森林面积变为,则,若需要植树造林x年,使得森林面积变为原来的5倍以上,则有,即,则有,所以为使森林面积变为原来的5倍以上,至少需要植树造林12年.故答案为:12.16.已知函数在区间内恰有一个零点,则实数的取值范围是__________________.【答案】【解析】当时,,令得,符合题意;当时,是二次函数,对于方程,只需,即,解得,且,当时,,此时,得或,符合题意,当时,,此时,得或,符合题意,综上,实数的取值范围为.故答案为:.四、解答题:解答应写出文字说明、证明过程或演算步骤.17.已知不等式的解集为.(1)求不等式的解集;(2)设非空集合,若是的充分不必要条件,求的取值范围.解:(1)因为不等式的解集为,所以方程的解为,所以,,得,,则不等式即,解得,故解集.(2)由(1)知,,而是的充分不必要条件,则是的真子集,所以,解得,综上所述,的取值范围是.18.已知,,且,.(1)求,;(2)求.解:(1)由题意知,,因为,所以,所以,所以.(2)由,,可得,,所以,,因为,所以.19.已知函数是奇函数.(1)求实数的值;(2)求关于的不等式的解集.解:(1)因为是奇函数,所以对定义域内的任意恒成立,则对任意定义域内的任意恒成立,所以,,当时,定义域为,不关于原点对称,舍去,当时,,符合条件,所以.(2),的定义域为,当时,,解得,当时,,解得,综上,当时,原不等式的解集为;当时,原不等式的解集为.20.某工厂生产某种产品,受生产能力、技术水平以及机器设备老化等问题的影响,每天都会生产出一些次品,根据对以往产品中次品的分析,得出每日次品数(万件)与日产量(万件)之间满足关系式(其中为小于6的正常数).对以往的销售和利润情况进行分析,知道每生产1万件合格品可以盈利4万元,但每生产1万件次
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 城市更新的空间布局与规划设计方案
- 3 夜市美食勾画的城市风情
- 农机操作面试试题及答案
- 胃溃疡相关考试题及答案
- 工厂安全文化
- 森林探险与野生动植物观赏行业跨境出海战略研究报告
- 2024年中国地质调查局西安地质调查中心招聘考试真题
- 工业托盘再生塑料制造行业跨境出海战略研究报告
- 敏感肌防晒霜棒企业制定与实施新质生产力战略研究报告
- 高压水流面部清洁器企业制定与实施新质生产力战略研究报告
- 《乡镇履职事项清单》(涵盖18个部门核心职责)
- 服装数字化设计技术课件 3-1男衬衫款式分析
- TSCNA 0001-2024 成人体外膜肺氧合(ECMO)技术护理规范
- 2025新人教版七年级历史下教案-第6课 隋唐时期的中外文化交流
- 光伏2021施工上岗证考核答案
- 2025年内蒙古交通职业技术学院单招职业适应性测试题库含答案
- 河南2025年河南职业技术学院招聘30人笔试历年参考题库附带答案详解
- 大班安全教育:不攀爬高处
- 急诊危重症患者转运专家共识解读课件
- 《混凝土预制构件出厂验收标准》
- 2025年数字安徽有限责任公司招聘笔试参考题库含答案解析

评论
0/150
提交评论