专题21二次函数与三角函数综合问题（原卷版）

挑战2023年中考数学压轴题之学霸秘笈大揭秘（全国通用）

专题21二次函数与三角函数综合问题

【例1】（2022•泰安二模）抛物线yx22xm的顶点A在x轴上，与y轴交于点B．

（1）求抛物线的解析式；

AB1

（2）如图1，直线CD//AB交抛物线于C，D两点，若，求COD的面积；

CD3

（3）如图2，已知（2）中C点坐标，点P是第二象限抛物线上一点，是否存在点P，使得tanPCO2，若存

在，请求出点P坐标，若不存在，请说明理由．

第1页共25页.

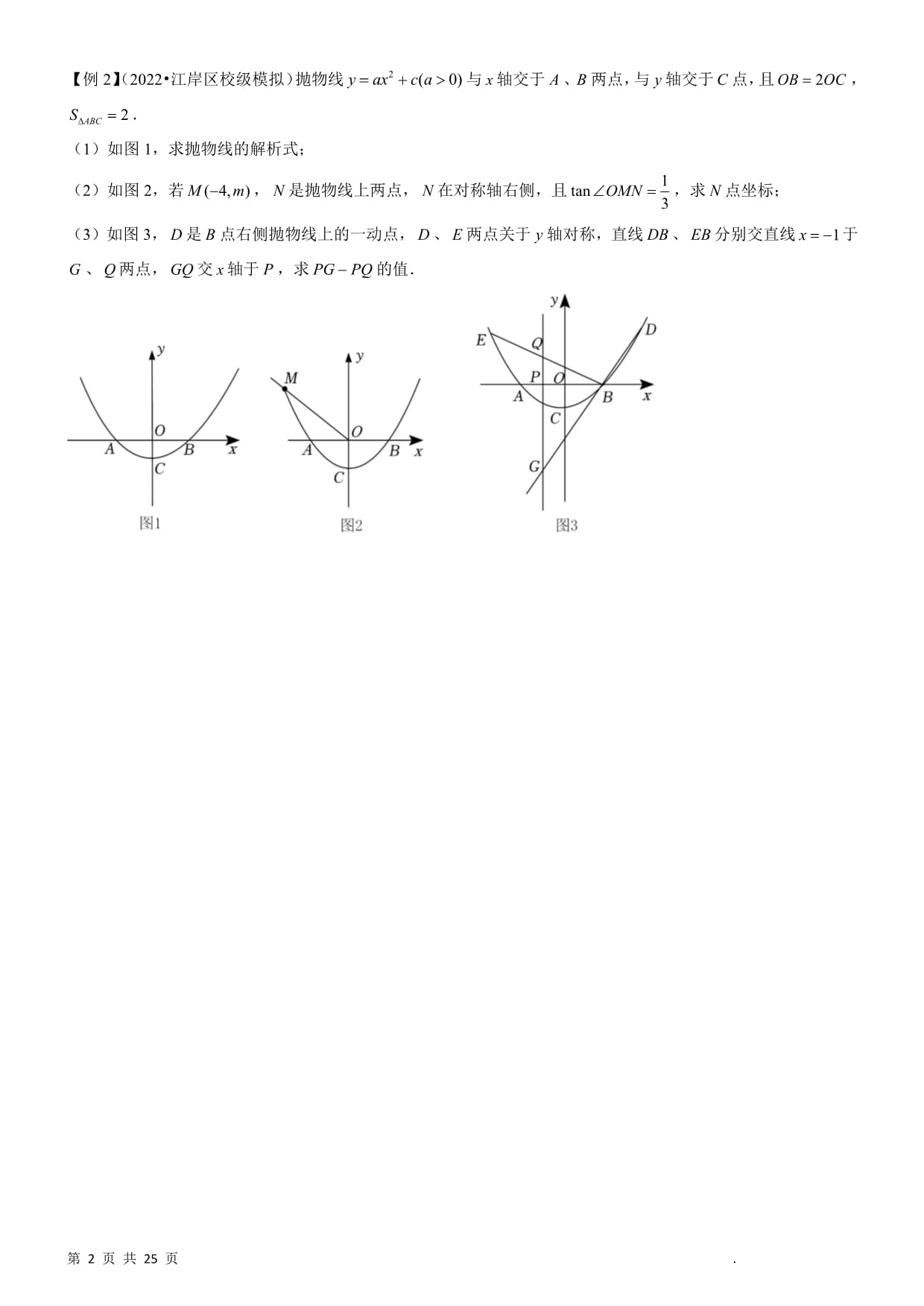
【例2】（2022•江岸区校级模拟）抛物线yax2c(a0)与x轴交于A、B两点，与y轴交于C点，且OB2OC，

．

SABC2

（1）如图1，求抛物线的解析式；

1

（2）如图2，若M(4,m)，N是抛物线上两点，N在对称轴右侧，且tanOMN，求N点坐标；

3

（3）如图3，D是B点右侧抛物线上的一动点，D、E两点关于y轴对称，直线DB、EB分别交直线x1于

G、Q两点，GQ交x轴于P，求PGPQ的值．

第2页共25页.

【例3】（2022•沈阳模拟）如图1，直线yx3分别交x轴，y轴于点B，C，经过点B，C的抛物线yx2bxc

交x轴正半轴于点A．

（1）求抛物线的函数表达式；

（2）如图2，D是第三象限内的抛物线上动点，DE//y轴交直线BC于点E，若CDE是等腰三角形，求点D

坐标；

1

（3）F是抛物线的顶点，直线BC上存在点M，使tanFMO，请直接写出点M坐标．

2

第3页共25页.

【例4】（2022•湖北）抛物线yx24x与直线yx交于原点O和点B，与x轴交于另一点A，顶点为D．

（1）直接写出点B和点D的坐标；

1

（2）如图1，连接OD，P为x轴上的动点，当tanPDO时，求点P的坐标；

2

（3）如图2，M是点B关于抛物线对称轴的对称点，Q是抛物线上的动点，它的横坐标为m(0m5)，连接MQ，

S

，与直线交于点．设和的面积分别为和，求1的最大值．

BQMQOBEBEQBEMS1S2

S2

第4页共25页.

1

【例5】（2022•南充）抛物线yx2bxc与x轴分别交于点A，B(4,0)，与y轴交于点C(0,4)．

3

（1）求抛物线的解析式．

（2）如图1，BCPQ顶点P在抛物线上，如果BCPQ面积为某值时，符合条件的点P有且只有三个，求点P

的坐标．

（3）如图2，点M在第二象限的抛物线上，点N在MO延长线上，OM2ON，连接BN并延长到点D，使

NDNB．MD交x轴于点E，DEB与DBE均为锐角，tanDEB2tanDBE，求点M的坐标．

第5页共25页.

1

【例6】（2022•无锡）已知二次函数yx2bxc图象的对称轴与x轴交于点A(1,0)，图象与y轴交于点B(0,3)，

4

C、D为该二次函数图象上的两个动点（点C在点D的左侧），且CAD90．

（1）求该二次函数的表达式；

（2）若点C与点B重合，求tanCDA的值；

（3）点C是否存在其他的位置，使得tanCDA的值与（2）中所求的值相等？若存在，请求出点C的坐标；若

不存在，请说明理由．

第6页共25页.

一．解答题（共20题）

1．（2022秋•工业园区期中）已知抛物线yax22axc的图象与x轴交于A、B两点（点A在点B的左侧），

与y轴正半轴交于C点，顶点为M，直线MDx轴于点D．

3

（1）当a0时，知OCMD，求AB的长；

4

（2）当a0时，若OCOB，tanACB2，求抛物线的解析式；

2．（2022春•德化县期中）在平面直角坐标系xOy中，经过原点O的抛物线yax2bxc(a0)与x轴的正半

轴交于点A(2m,0)，P为抛物线的顶点，且tanOAP2．

（1）已知m2．

①求二次函数的解析式；

②直线l:ykxb平行于AP，且将OAP分成面积相等的两部分，求直线l的解析式．

（2）若Q为对称轴右侧的二次函数图象上的一点，且直线AQ交对称轴于点B，点B，C关于点P对称，求证：

直线CQ过定点．

第7页共25页.

3．（2021秋•朝阳区校级期中）如图，已知抛物线yax22axc(a0)与y轴交于点C(0,3)，与x轴交于点A、

B，

（1）若点A的坐标为(3,0)；

①求该抛物线的解析式．

②tanCBO；

③点D是线段AB上的动点．过点D作DE//AC，交线段BC于点E，连接CD，设点D的横坐标为m，CDE

的面积为S，求S关于m的函数关系式；当CDE的面积最大时，求点D的坐标；

（）已知、是抛物线上两点；将抛物线上位于、两点间的部分记为；把的最高点

2M(1,y1)N(2,y2)MNGG

与最低点的纵坐标的差记为d，当2„d„5时，求a的取值范围．

第8页共25页.

4．（2022•长春模拟）在平面直角坐标系中，抛物线yax22ax3a(a0)的顶点为P，且该抛物线与x轴交于

A、B两点（点A在点B的左侧）．我们规定抛物线与x轴围成的封闭区域称为“区域G”（不包括边界）；横、

纵坐标都是整数的点称为整点．

（1）如果抛物线yax22ax3a经过点(1,3)．

①求a的值；

②直接写出“区域G”内整数点的个数；

（2）当a0时，如果抛物线yax22ax3a在“区域G”内有4个整数点，求a的取值范围；

（3）当a0时，抛物线与直线xa交于点C，把点C向左平移5个单位长度得到点D，以CD为边作等腰直

角三角形CDE，使DCE90，点E与抛物线的顶点始终在CD的两侧，线段DE与抛物线交于点F，当

2

tanECF时，直接写出a的值．

3

第9页共25页.

5．（2022•长沙二模）如果三角形的两个内角与满足290，那么我们称这样的三角形为“CJ三角形”．

（1）判断下列三角形是否为“CJ三角形”？如果是，请在对应横线上画“”，如果不是，请在对应横线上画

“”；

①其中有两内角分别为30，60的三角形；

②其中有两内角分别为50，60的三角形；

③其中有两内角分别为70，100的三角形；

k

（2）如图1，点A在双曲线y(k0)上且横坐标为1，点B(4,0)，C为OB中点，D为y轴负半轴上一点，

x

若OAB90．

①求k的值，并求证：ABC为“CJ三角形”；

②若OAB与OBD相似，直接写出D的坐标；

（3）如图2，在RtABC中，ACB90，AC6，BC8，E为BC边上一点，BECE且ABE是“CJ三

角形”，已知A(6,0)，记BEt，过A，E作抛物线yax2bxc(a0)，B在A右侧，且在x轴上，点Q在

1

抛物线上，使得tanABQ，若符合条件的Q点个数为3个，求抛物线yax2bxc的解析式．

t3

第10页共25页.

6．如图，抛物线yax2bx2(a0)与x轴交于点A(1,0)，B(2,0)，与y轴交于点C，点F是抛物线上一动

点，过点B，C作直线BC．

（1）求抛物线的解析式及tanCBO的值；

2

（2）当点F到直线BC的距离为时，求点F的坐标；

2

（3）过点F作FEx轴于点E，交直线BC于点D，若FCDACO45，求点F的坐标．

第11页共25页.

7．（2022•中山市三模）如图，抛物线yax2bx3与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴

4

为直线x1，点A(1,0)，过B的直线交y轴于点D，交抛物线于E，且tanEBA．

3

（1）求抛物线的解析式；

（2）在抛物线第四象限的图象上找一点P，使得BDP的面积最大，求出点P的坐标；

4

（3）点M是线段BE上的一点，求AMME的最小值，并求出此时点M的坐标．

5

第12页共25页.

8．（2022•松江区校级模拟）如图，在平面直角坐标系xOy中，点A、点B分别在x的正半轴和y的正半轴上，

tanOAB3，抛物线yx2mx3经过A、B两点，顶点为D．

（1）求抛物线的表达式；

（2）将OAB绕点A顺时针旋转90后，点B落到点C的位置，求四边形ABCD的面积；

（3）将该抛物线沿y轴向上或向下平移，使其经过点C，若点P在平移后的抛物线上，且满足ACPABO，

求点P的坐标．

第13页共25页.

9．（2022•沈阳模拟）如图，已知点A(4,0)，点B(2,1)，直线y2xb过点B，交y轴于点C，抛物线

15

yax2xc经过点A，C．

4

（1）求抛物线的解析式；

4

（2）D为直线AC上方的抛物线上一点，且tanACD，求点D的坐标；

3

1

（3）平面内任意一点P，与点O距离始终为2，连接PA，PC．直接写出PAPC的最小值．

2

第14页共25页.

3

10．（2022春•西山区校级月考）已知对称轴为直线x的抛物线经过A(1,0)，C(0,4)两点，抛物线与x轴的

2

另一个交点为B．

（1）求抛物线的解析式；

SPBD

（2）如图1，若点P为第四象限抛物线上一点，连接OP，BC交于点D，连接BP，求的最大值；

SOBD

1

（3）如图2，若点Q为抛物线上一点，且当tanBCQ，求点Q的坐标．

4

第15页共25页.

11．（2022春•汉川市校级月考）如图，在平面直角坐标系中，顶点为A(2cos60,2sin45)的抛物线经过点B(5,3)，

且与x轴交于C，D两点（点C在点D的左侧）．

（1）求抛物线的解析式；

（2）求tanAOB的值；

（3）点M在第二象限内的抛物线上，点N在x轴上，且MNDOAB，当DMN与OAB相似时，求点M的

坐标．

第16页共25页.

12．（2022秋•道里区校级期中）如图，在平面直角坐标系中，点O为坐标原点，直线yx3交x轴于点A，y

轴于点D，抛物线yx2bx3与x轴交于A，B两点，交y轴于点C．

（1）求抛物线的解析式；

（2）P在第三象限抛物线上，P点横坐标为t，连接AP、DP，APD的面积为s，求s关于t的函数关系式；

（不要求写自变量t的取值范围）

（3）在（2）的条件下，PD绕点P逆时针旋转，与线段AD相交于点E，且EPD2PDC，过点E作EFPD

1

交PD于G，y轴于点F，连接PF，若sinPFC，求线段PF的长．

3

第17页共25页.

13．（2022•荆门模拟）抛物线yax2bxc与x轴交于点A(1,0)和点B，与y轴交于点C，顶点D的坐标为

(1,4)．

（1）求抛物线的解析式；

（2）如图，点P(m,n)在第一象限的抛物线上，且mn9，求点P的坐标；在线段PA上确定一点M，使DM

平分四边形ACDP的面积，求点M的坐标；

（3）点Q是抛物线对称轴上的一个动点，连接OQ、AQ，设AOQ的外心为H，当sinOQA的值最大时，请

直接写出点H的坐标．

第18页共25页.

14．（2022春•磐安县期中）如图，抛物线yax2bxc(a0)与x轴交于点A(1,0)，B(9,0)，与y轴交于点C，

已知OACOCB．

（1）求抛物线的函数表达式；

（2）若点P在y轴上，在该抛物线的对称轴上，是否存在唯一的点Q，满足AQP90？如果存在，请求出点

P的坐标；如果不存在，请说明理由；

2

（3）若点P在y轴上，满足sinAPB的点P是否存在？如果存在，请求出点P的坐标；如果不存在，请说

3

明理由．

第19页共25页.

15．（2022•合肥模拟）如图，在平面直角坐标系中，抛物线yax2bxc(a0)与x轴交于点A(2,0)，B(4,0)，

33

与直线yx3交于y轴上的点C，直线yx3与x轴交于点D．

22

（1）求该抛物线的解析式；

（2）点P是抛物线上第一象限内的一一个动点，连接PC、PD，当PCD的面积最大时，求点P的坐标；

（3）将抛物线的对称轴向左平移3个长度单位得到直线l，点E是直线l上一点，连接OE、BE，若直线l上存

在使sinBEO最大的点E，请直接写出满足条件的点E的坐标；若不存在，请说明理由．

第20页共25页.

16．（2022•高州市一模）在平面直角坐标系xOy中，已知抛物线yax2bx3与x轴交于A(1,0)、B(3,0)两点，

与y轴交于C点，D为抛物线顶点．

（1）求该抛物线的解析式．

（2）如图1，连接AD，交y轴于点E，点P是第一象限的抛物线上的一个动点，连接PD交x轴于F，连接EF、

，若，求点的坐标．

APSADP3SDEFP

（3）点Q是抛物线对称轴上一动点，连接OQ、AQ，设AOQ外接圆圆心为H，当sinOQA的值最大时，请

求出点H的坐标．

第21页共25页.

17．（2022•夏津县模拟）如图，抛物线yax2bx2与x轴交于A，B两点，且OA2OB，与y轴交于点C，

1

连接BC，抛物线对称轴为直线x．D为第一象限内抛物线上一动点，过点D作DEOA于点E，与AC交

2

于点F，设点D的横坐标为m．

（1）求抛物线的表达式；

（2）当线段DF的长度最大时，求sinDCF的值；

（3）点P是抛物线对称轴上的一点，点G是坐标平面内的一点，是否存在点P，使得以点P，B，C，G为

顶点的四边形是菱形，若存在，请直接写出点P的坐标；若不存在，请说明理由．

第22页共25页.

18．（2022•黄冈模拟）如图，在平面直角坐标系中，抛物线yax2bx2与x轴交点为A(4,0)、B(1,0)，与y

轴交于点C，P为抛物线上一点，过点P作PDAC于D．

（1）求抛物线的解析式；

（2）如图1，若P在直线AC上方，PEx轴于E，交AC于F．

①求sinPFD的值；

②求线段PD的最大值．

（3）如图2，连接PC，当PCD与ACO相似时，直接写出点P的坐标．

第23页共25页.

19．（2022•广东模拟）在平面直角坐标系xOy中，已知抛物线