新教材适用2024-2025学年高中数学第8章成对数据的统计分析8.3列联表与独立性检验素养作业新人教A版选择性必修第三册

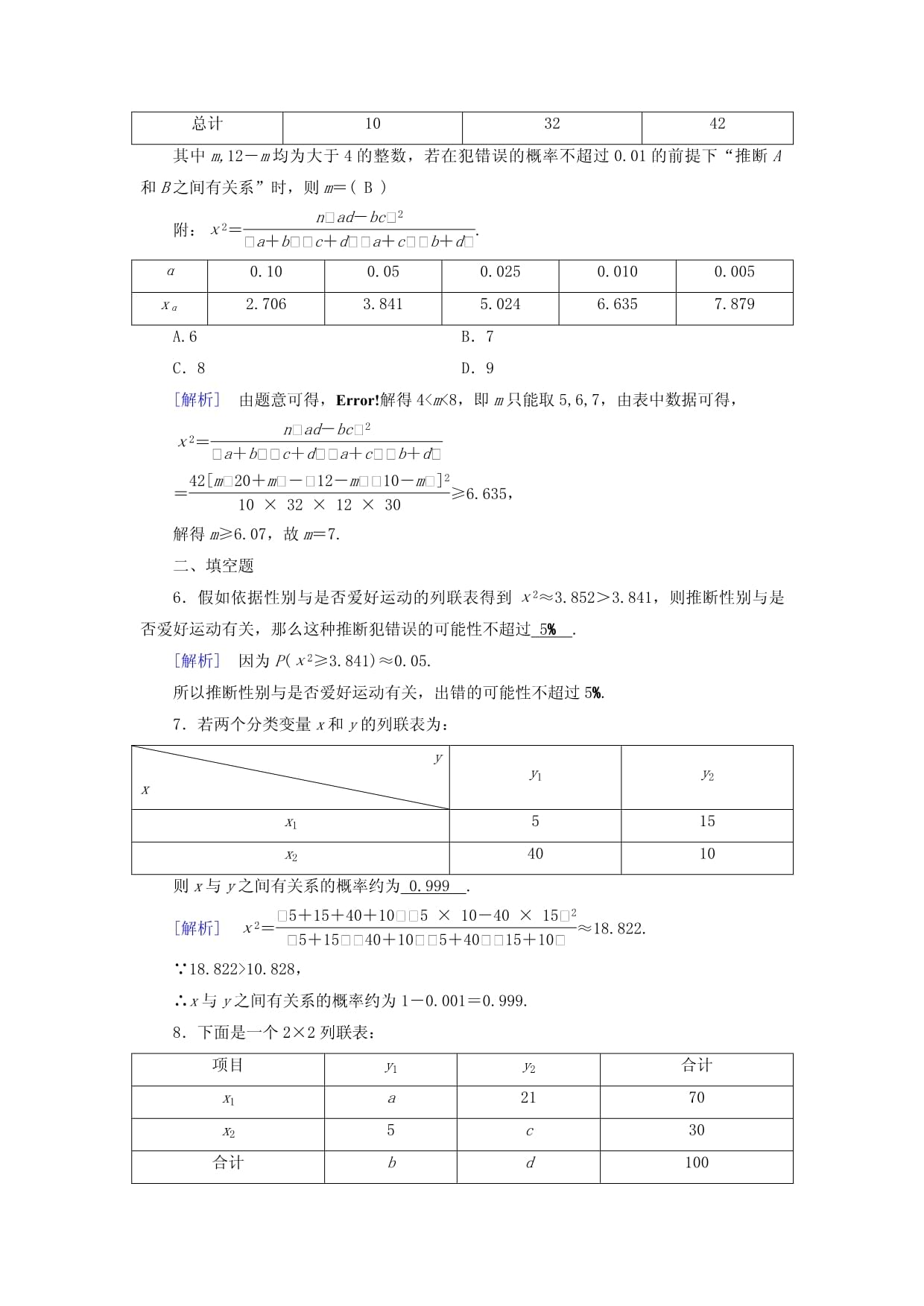
第八章8.3A组·基础自测一、选择题1．(多选)下列说法正确的是(AB)A．事务A与B独立，即两个事务互不影响B．事务A与B关系越亲密，则χ2就越大C．χ2的大小是判定事务A与B是否相关的唯一依据D．若判定两事务A与B相关，则A发生B肯定发生[解析]由事务的独立性知，A选项正确；由独立性检验的意义知，B选项正确；χ2的大小是判定事务A与B是否相关的一种方法，不是唯一依据，C选项不正确；若事务A与B相关，则A发生B可能发生，也可能不发生，D选项不正确．2．分类变量X和Y的列表如下，则下列说法推断正确的是(C)y1y2合计x1aba＋bx2cdc＋d合计a＋cb＋da＋b＋c＋dA.ad－bc越小，说明X和Y关系越弱B．ad－bc越大，说明X和Y关系越强C．(ad－bc)2越大，说明X与Y关系越强D．(ad－bc)2越接近于0，说明X与Y关系越强[解析]列联表可以较为精确地推断两个变量之间的相关关系程度，由χ2＝eq\f(a＋b＋c＋dad－bc2,a＋ba＋cb＋dc＋d)，当(ad－bc)2越大，χ2越大，表明X与Y的关系越强．(ad－bc)2越接近0，说明两个分类变量X和Y无关的可能性越大．3．为考察某种药物对预防禽流感的效果，在四个不同的试验室取相同的个体进行动物试验，依据四个试验室得到的列联表画出如下四个等高积累条形图，最能体现该药物对预防禽流感有显著效果的图形是(D)[解析]分析四个等高条形图得选项D中，不服用药物患病的概率最大，服用药物患病的概率最小，所以最能体现该药物对预防禽流感有显著效果，故选D.4．为了了解手机品牌的选择是否和年龄的大小有关，随机抽取部分A品牌手机运用者和B品牌手机运用者进行统计，统计结果如下表：年龄手机品牌合计A品牌B品牌30岁以上40206030岁以下(含30岁)152540合计5545100依据表格计算得χ2≈8.249，据此推断下列结论正确的是(C)A．没有任何把握认为“手机品牌的选择与年龄大小有关”B．可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”C．可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”D．可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小无关”[解析]χ2≈8.249>6.635＝x0.01，由小概率值α＝0.01的独立性检验知，在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”．5．已知随机事务A与B的样本数据的2×2列联表如下：项目Aeq\x\to(A)总计Bm12－m12eq\x\to(B)10－m20＋m30总计103242其中m,12－m均为大于4的整数，若在犯错误的概率不超过0.01的前提下“推断A和B之间有关系”时，则m＝(B)附：χ2＝eq\f(nad－bc2,a＋bc＋da＋cb＋d).α0.100.050.0250.0100.005xα2.7063.8415.0246.6357.879A.6 B．7C．8 D．9[解析]由题意可得，eq\b\lc\{\rc\(\a\vs4\al\co1(m>4，,12－m>4，))解得4<m<8，即m只能取5,6,7，由表中数据可得，χ2＝eq\f(nad－bc2,a＋bc＋da＋cb＋d)＝eq\f(42[m20＋m－12－m10－m]2,10×32×12×30)≥6.635，解得m≥6.07，故m＝7.二、填空题6．假如依据性别与是否爱好运动的列联表得到χ2≈3.852＞3.841，则推断性别与是否爱好运动有关，那么这种推断犯错误的可能性不超过5%.[解析]因为P(χ2≥3.841)≈0.05.所以推断性别与是否爱好运动有关，出错的可能性不超过5%.7．若两个分类变量x和y的列联表为：yxy1y2x1515x24010则x与y之间有关系的概率约为0.999.[解析]χ2＝eq\f(5＋15＋40＋105×10－40×152,5＋1540＋105＋4015＋10)≈18.822.∵18.822>10.828，∴x与y之间有关系的概率约为1－0.001＝0.999.8．下面是一个2×2列联表：项目y1y2合计x1a2170x25c30合计bd100则b－d＝_8__，χ2≈_24.047__.(保留小数点后3位)[解析]由2×2列联表得：a＝49，b＝54，c＝25，d＝46.所以b－d＝54－46＝8.χ2＝eq\f(100×49×25－5×212,70×30×54×46)≈24.047.三、解答题9．甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量状况统计如下表：一级品二级品合计甲机床15050200乙机床12080200合计270130400(1)甲机床、乙机床生产的产品中一级品的频率分别是多少？(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异？附：K2＝eq\f(nad－bc2,a＋bc＋da＋cb＋d)，P(K2≥k)0.0500.0100.001k3.8416.63510.828[解析](1)依据题表中数据知，甲机床生产的产品中一级品的频率是eq\f(150,200)＝0.75，乙机床生产的产品中一级品的频率是eq\f(120,200)＝0.6.(2)依据题表中的数据可得K2＝eq\f(400×150×80－120×502,200×200×270×130)＝eq\f(400,39)≈10.256.因为10.256>6.635，所以有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异．10．为加强环境爱护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的PM2.5和SO2浓度(单位：μg/m3)，得下表：SO2PM2.5[0,50](50,150](150,475][0,35]32184(35,75]6812(75,115]3710(1)估计事务“该市一天空气中PM2.5浓度不超过75，且SO2浓度不超过150”的概率；(2)依据所给数据，完成下面的2×2列联表：SO2PM2.5[0,150](150,475][0,75](75,115](3)依据(2)中的列联表，依据小概率α＝0.01的独立性检验，推断该市一天空气中PM2.5浓度与SO2浓度是否有关？[解析](1)依据抽查数据，该市100天的空气中PM2.5浓度不超过75，且SO2浓度不超过150的天数为32＋18＋6＋8＝64，因此，该市一天空气中PM2.5浓度不超过75，且SO2浓度不超过150的概率的估计值为eq\f(64,100)＝0.64.(2)依据抽查数据，可得2×2列联表：SO2PM2.5[0,150](150,475][0,75]6416(75,115]1010(3)零假设H0：该市一天空气中PM2.5浓度与SO2浓度无关．依据(2)的列联表得χ2＝eq\f(100×64×10－16×102,80×20×74×26)≈7.484>6.635＝x0.01.依据小概率值α＝0.01的独立性检验，我们认为H0不成立，即认为该市一天空气中PM2.5浓度与SO2浓度有关，此推断犯错误的概率不超过0.01.B组·实力提升一、选择题1．(多选)晚上睡眠足够是提高学习效率的必要条件．某中学高二的学生分为寄宿生和走读生两类，其中寄宿生晚上9：50必需休息，睡眠能得到充分的保证；走读生晚上大多10：30休息，甚至更晚．为了了解这两类学生的学习效率状况，该校有关部门分别对这两类学生学习总成果的前50名进行问卷调查，得到如表所示的统计数据，则下列说法正确的是(BC)学习效率寄宿生走读生效率高3010效率低2040A.走读生前50名学生中有40%的学生学习效率高B．寄宿生前50名学生中有60%的学生学习效率高C．依据α＝0.001的独立性检验，可以认为“学生学习效率凹凸与晚上睡眠是否足够”有关D．依据α＝0.001的独立性检验，可以认为“学生学习效率凹凸与晚上睡眠是否足够”无关[解析]对于A，P(走读生学习效率高)＝eq\f(10,50)＝20%，故选项A错误；对于B，P(寄宿生学习效率高)＝eq\f(30,50)＝60%，故选项B正确；对于C，零假设为H0：学生学习效率凹凸与晚上睡眠是否足够无关．依据列联表中的数据，经计算得到χ2＝eq\f(100×30×40－10×202,30＋10×30＋20×10＋40×20＋40)≈16.667>10.828＝x0.001，依据α＝0.001的独立性检验，我们推断H0不成立，即认为“学生学习效率凹凸与晚上睡眠是否足够”有关，该推断犯错误的概率不超过0.001.故选项C正确，选项D错误．2．(多选)有两个分类变量X，Y，其列联表如下所示，Y1Y2X1a20－aX215－a30＋a其中a,15－a均为大于5的整数，若在犯错误的概率不超过0.05的前提下认为X，Y有关，则a的值为(CD)A．6 B．7C．8 D．9[解析]依据公式，得χ2＝eq\f(65×[a30＋a－15－a20－a]2,20×45×15×50)＝eq\f(13×13a－602,20×45×3×2)>3.841，依据a>5且15－a>5，a∈Z，求得当a＝8或9时满意题意．3．某校团委对“学生性别和喜爱某热门软件是否有关联”进行了一次调查，其中被调查的女生人数是男生人数的eq\f(1,2)，男生喜爱该软件的人数占男生人数的eq\f(1,6)，女生喜爱该软件的人数占女生人数的eq\f(2,3).若有99%的把握认为喜爱该软件和性别有关联，则男生至少有(B)参考公式：χ2＝eq\f(nad－bc2,a＋bc＋da＋cb＋d)，其中n＝a＋b＋c＋d.α0.100.050.0250.0100.0050.001xα2.7063.8415.0246.6357.87910.828A.12人 B．18人C．24人 D．30人[解析]设男生人数为x，女生人数为eq\f(x,2).作出2×2列联表：喜爱该软件不喜爱该软件合计男生eq\f(1,6)xeq\f(5,6)xx女生eq\f(1,3)xeq\f(1,6)xeq\f(x,2)合计eq\f(x,2)xeq\f(3,2)x可得χ2＝eq\f(\f(3x,2)\b\lc\(\rc\)(\a\vs4\al\co1(\f(x,6)·\f(x,6)－\f(x,3)·\f(5x,6)))2,\f(x,2)·x·\f(x,2)·x)＝eq\f(3x,8)>6.635.解得x>17.69，∵x为整数，所以，若在犯错误的概率不超过0.01的前提下认为是否喜爱该软件和性别有关，则男生至少有18人．故选B.二、填空题4．某校在两个班进行教学方式对比试验，两个月后进行了一次检测，试验班与比照班成果统计如表所示(单位：人)：80及80分以上80分以下总计试验班351550比照班20m50总计5545n(1)m＝30，n＝100；(2)依据表中数据得到的结论是有99%的把握说“教学方式与成果有关系”.[解析](1)m＝45－15＝30，n＝50＋50＝100.(2)由表中的数据得χ2＝eq\f(100×35×30－15×202,50×50×55×45)≈9.091.因为9.091>6.635，所以有99%的把握说“教学方式与成果有关系”．5．如图所示是调查某学校高一、高二年级学生参与社团活动的等高积累条形图，阴影部分的高表示参与社团的频率．已知该校高一、高二年级学生人数均为600人(全部学生都参与了调查)，现从参与社团的同学中按分层随机抽样的方式抽取45人，则抽取的高二学生人数为_27__.[解析]依据等高积累条形图可知，参与社团的高一和高二年级学生的人数比为2∶3，由分层随机抽样的性质可得抽取的高二学生人数为45×eq\f(3,5)＝27.三、解答题6．海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量(单位：kg)，其频率分布直方图如图．(1)设两种养殖方法的箱产量相互独立，记A表示事务“旧养殖法的箱产量低于50kg，新养殖法的箱产量不低于50kg”，估计A的概率；(2)填写下面列联表，并依据列联表推断是否有99%的把握认为箱产量与养殖方法有关.箱产量<50kg箱产量≥50kg旧养殖法新养殖法附：P(χ2≥k)0.0500.0100.001k3.8416.63510.828χ2＝eq\f(nad－bc2,a＋bc＋da＋cb＋d).[解析](1)记B表示事务“旧养殖法的箱产量低于50kg”，C表示事务“新养殖法的箱产量不低于50kg”，∴P(A)＝P(BC)＝P(B)P(C)，旧养殖法的箱产量低于50kg的频率为(0.012＋0.014＋0.024＋0.034＋0.040)×5＝0.62，故P(B)的估计值为0.62，新养殖法的箱产量不低于50kg的频率为(0.068＋0.046＋0.010＋0.008)×5＝0.66，故P(C)的估计值为0.66，则事务A的概率估计值为P(A)＝P(B)·P(C)＝0．62×0.66＝0.4092，∴A发生的概率为0.4092.(2)依据箱产量的频率分布直方图得到列联表：箱产量<50kg箱产量≥50kg总计旧养殖法6238100新养殖法3466100总计96104200则χ2＝eq\f(200×62×66－38×342,1